一种基于托卡马克中多组分等离子体辐射效应的粒子演化模拟方法

1.本发明属于磁约束受控核聚变技术领域，特别涉及一种用于托卡马克中多组分等离子体辐射效应的粒子密度分布演化的方法。


背景技术：

2.近年来，由于世界人口的急剧增加，生产力和生产技术都得到了有效提升，因此人类对能源的消耗也在急剧增加，从而导致那些不可再生的化石能源日益枯竭。很明显，这导致了近些年来人类赖以生存的环境逐渐恶化，造成了温室效应的快速加剧，一些反常天气以及恶劣的自然现象也层出不穷。所以，对清洁能源的寻找与使用成为了科学家们的不断追求。目前，核能是相对高效无污染的能源，我国所提出的核能战略是：近期建造热中子堆，中期使用快中子堆，远期建设聚变堆。这里的聚变堆指的就是磁约束受控核聚变。要想实现磁约束受控核聚变，就要完全掌握其稳态运行机理，同时要充分了解并解决内部等离子体间相互作用产生的一些不稳定性、等离子体与托卡马克器壁的相互作用以及一些其它可以促进能量损失致使放电熄灭的各种复杂问题。因此，研究最先进的磁场位形下的托卡马克能量损失也就颇为重要。
3.先进的磁场位形可以更容易地束缚等离子体，进而实现稳定的长脉冲放电，最终实现其商用价值。在托卡马克等离子体中，作为托卡马克的主要能量损失机制之一的等离子体辐射，是指等离子体在各个频段所发射出来的电磁波。而辐射所在的光谱主要包括连续谱和线状谱，对应的辐射也就称之为连续性辐射和线辐射。连续性辐射的主要代表是轫致辐射，线辐射主要包括电子回旋辐射和特征线辐射。特征线辐射主要来自杂质离子辐射。总体来看，辐射光谱涵盖了从红外到x射线的所有波段。在未来的大型磁约束核聚变装置中，高z
eff
的金属杂质辐射是非常重要的，它对等离子体中的磁流体力学不稳定性会产生很影响。因此，研究等离子体辐射、清晰地掌握等离子体辐射的每一个特性对实现长脉冲放电在当下也就尤为重要。所以，本发明基于此提出了一种可以用于计算在先进磁场位形下，将多种等离子体辐射效应耦合在一起的模拟方法，同时考虑了杂质粒子、电子以及离子的分布演化对等离子体总辐射的影响，从而可以对托卡马克放电中的磁流体力学不稳定性方面进行数值模拟研究，此方法计算效率高且数值稳定性强，也可以与实验中通过谱线的测量所得到的等离子体辐射功率进行对比分析，从而为日后实现磁约束核聚变打下坚实的基础。


技术实现要素：

4.为了填补托卡马克中对等离子体辐射数值模拟的技术空白，本发明提供了一种用于先进磁场位形下托卡马克中等离子体辐射的粒子密度分布演化的模拟方法，也就是说，计算等离子体辐射中用到的粒子都是随时间演化的。该方法可以很好地与实验结合，通过对杂质密度分布演化、电子密度分布演化以及离子密度分布演化的计算得到杂质、电子以
及离子实时动态分布，可以更加精确地对等离子体辐射进行预测与模拟，并且实现了等离子体辐射非线性演化的三维模拟，进而可以系统地研究等离子体辐射在先进磁场位形下对托卡马克放电的影响，同时也可以为等离子体辐射的实验结果提供参考。
5.本发明采用的技术方案：
6.一种基于托卡马克中多组分等离子体辐射效应的粒子演化模拟方法，实现了电子、离子和杂质密度分布的演化，进而可以得出多种等离子体辐射在真实三维磁场位形下的非线性演化，同时也能够得到任意时刻的等离子体辐射的演化情况以及等离子体相关参数的演化剖面，可以更加准确地描述在先进磁场位形下多种等离子体辐射共同作用下托卡马克等离子体的空间分布情况。该方法具体包括以下步骤：
7.步骤1：将托卡马克装置放电实验中的等离子体区域进行网格划分，等离子体辐射演化过程中得到的等离子体总辐射值、磁通函数值等均可以由所划分的网格节点进行数据的存储。
8.步骤2：根据实验中最高电离态、远红外干涉仪与汤姆逊散射来分别计算出初始杂质密度分布初始电子密度分布和初始电子温度分布
9.步骤3：托卡马克放电中采用磁通环等设备来得到初始磁场的位形，并通过数值模拟法等计算得到初始磁通ψ
(0)
并存储在网格节点中。
10.步骤4：将初始磁通ψ
(0)
、初始杂质密度分布初始电子密度分布和初始离子密度分布(根据实际研究情况给定)分别带入到磁流体方程、杂质密度分布演化方程、电子密度分布演化方程和离子密度分布演化方程中进行计算，分别得到下一时刻的磁通ψ
(1)
、杂质密度分布电子密度分布和离子密度分布具体步骤如下：
11.杂质密度分布的演化方程为：
[0012][0013]
电子密度分布的演化方程为：
[0014][0015]
离子密度分布的演化方程为：
[0016][0017]
其中，nz为杂质的粒子密度分布，ne表示电子密度分布，ni表示离子密度分布；φ为电势，t为时间；d
z||
和dz⊥
分别是杂质的平行方向与垂直方向的杂质扩散系数；d
e||
和de⊥
分别是电子的平行方向与垂直方向的杂质扩散系数；d
i||
和di⊥
分别是离子的平行方向与垂直方向的杂质扩散系数；和分别是平行方向与垂直方向的梯度算符；s
radz
为杂质的源项，s
rade
为电子的源项，s
radi
为离子的源项。
[0018]
所述杂质密度分布、电子密度分布和离子密度分布演化方程的具体计算方法如
下：
[0019]
步骤4.1：将杂质密度分布、电子密度分布和离子密度分布用谱方法进行表达：
[0020][0021]
其中，(m,n)是环向与极向模数；r0为托卡马克的大半径；θ为极向角；z表示柱向方向；f为粒子分布，包括杂质密度分布、电子密度分布和离子密度分布。
[0022]
步骤4.2：采用两步预测-校正法进行各种粒子分布的时间推进计算。其中，两步预测-校正法的计算格式如下：
[0023]
预测：
[0024][0025]
校正：
[0026][0027]
其中，h表示磁通量以及磁流体方程中的参数；v为扩散系数；t为时间；代表半个时间步长；dt代表一个时间步长；下标rhs表示磁流体方程的右手项，表示垂直磁场方向的梯度。
[0028]
通过步骤4.1和4.2即可将杂质密度分布、电子密度分布和离子密度分布演化方程求解。之所以采用谱方法和预测-校正法是因为二者可以更加精确、快速且稳定地计算出每一时刻的杂质密度分布、电子密度分布和离子密度分布，进而将杂质密度分布的演化方程、电子密度分布的演化方程、离子密度分布的演化方程与磁流体方程进行耦合，可以自洽地计算出任意时刻的杂质、电子与离子的分布。
[0029]
步骤5：根据步骤4计算出杂质密度分布，当托卡马克芯部的杂质密度分布达到设定的阈值时，进而将等离子体辐射的计算模块打开，从而计算磁场位形随时间的演化并得到此时刻的等离子体总辐射具体步骤如下：
[0030]
步骤5.1：根据电子温度分布te的数值和产生的杂质种类计算出相对应的辐射冷却率l(te)的数值。
[0031]
步骤5.2：计算等离子体总辐射，包括连续性辐射和线辐射。
[0032]
根据连续性辐射公式：
[0033][0034]
和电子回旋辐射公式：
[0035]
pc＝5.4
×
10-25
neb2t
e erg s-1
cm-3
[0036]
以及特征线辐射的计算公式：
[0037]
pz＝nenz∑l(te)erg s-1
cm-3
[0038]
计算出三种辐射的大小，然后将三种辐射累加即可以得到等离子总辐射其中，pb表示连续性辐射的大小，pc表示电子回旋辐射的大小，pz表示线辐射的大小；z
eff
为有效电荷分布。
[0039]
步骤6：将计算出的等离子体总辐射耦合进磁流体方程中，计算一个单位时间步长下的磁通量的演化，并得到加入等离子体总辐射演化后的磁通量
[0040]
步骤7：将步骤5中计算得到的等离子体总辐射的三维空间分布信息输出。
[0041]
步骤8：根据步骤6中计算后得到的考虑等离子体总辐射后的磁通量进一步计算出当下的磁场位形，进而继续重复步骤5-8即得到任意时刻的等离子体总辐射以及考虑等离子体总辐射后的磁通量
[0042]
本发明的有益效果：本发明所述方法可以计算电子密度分布演化、离子密度分布演化与杂质密度分布演化，可以实时表征出托卡马克等离子体中各个参数的演化过程，同时能够计算多种等离子体辐射，从而可以对先进磁场位形下的托卡马克装置放电中的磁流体不稳定性方面展开数值模拟与分析，还可以为等离子体辐射的实验结果提供参考，计算效率高且数值稳定性强，是一种稳定高效的数值模拟方法。
附图说明
[0043]
图1为本发明所适用的托卡马克实验装置的三维真实磁场位形示意图，包含磁岛与等离子体总辐射。
[0044]
图2为本方法对在先进磁场位形下，经过杂质、电子和离子演化后计算出的等离子体总辐射随时间演化的空间分布的计算结果；其中，(a)为55τa时的辐射空间分布，(b)为60τa时的辐射空间分布，(c)为65τa时的辐射空间分布，(d)为75τa时的辐射空间分布。其中τa为阿尔芬时间。
[0045]
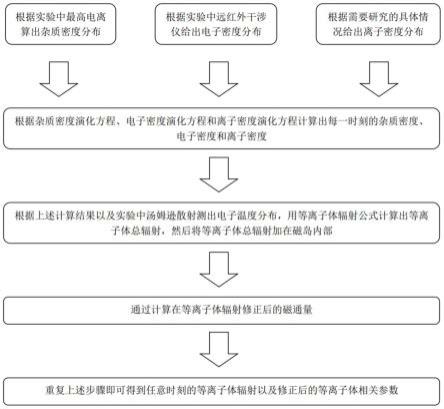
图3为本发明用于模拟计算先进磁场位形下多种等离子体辐射效应的方法主要流程图。
具体实施方式
[0046]
为了使本发明的目的、技术方案及优点更加清楚明白，下面将结合附图，对本发明的具体实施方式进行详细的描述。
[0047]
托卡马克装置是一个类似轮胎形状的一个环形装置，其示意图如图1所示，里面是一层层嵌套的磁面，同时磁力线沿着环向和极向的方向缠绕，在不稳定的情况下会产生磁岛。图2中表明，等离子体辐射的空间尺度是不断演化的，并且随着磁岛宽度的增加而增大，同时，杂质密度分布、电子密度分布和离子密度分布都是随时间演化的，因此本发明不仅可以计算托卡马克中杂质密度分布、电子密度分布和离子密度分布随时间的演化过程，还可以将多种等离子体辐射完整的加在磁岛内部，使得其随磁岛宽度的演化而自洽的非线性演化。
[0048]
具体实施步骤如下：
[0049]
步骤1：将托卡马克装置放电实验中的等离子体区域进行网格划分，等离子体辐射演化过程中得到的等离子体总辐射值、磁通函数值等均可以由所划分的网格节点进行数据的存储。
[0050]
步骤2：根据实验中最高电离态、远红外干涉仪与汤姆逊散射来分别计算出初始杂质密度分布初始电子密度分布和初始电子温度分布
[0051]
步骤3：托卡马克放电中采用磁通环来得到初始磁场的位形，并通过数值模拟法计算得到初始磁通ψ
(0)
并存储在网格节点中。
[0052]
步骤4：将初始磁通v
(0)
、初始杂质密度分布初始电子密度分布和初始离子密度分布(根据实际研究情况给定)分别带入到磁流体方程、杂质密度分布演化方程、电子密度分布演化方程和离子密度分布演化方程中进行计算，得到下一时刻的磁通ψ
(1)
、杂质密度分布电子密度分布和离子密度分布杂质密度分布、电子密度分布和离子密度分布演化方程的具体计算方法如下：
[0053]
杂质密度分布的演化方程为：
[0054][0055]
电子密度分布的演化方程为：
[0056][0057]
离子密度分布的演化方程为：
[0058][0059]
其中，nz为杂质的粒子密度分布，ne表示电子密度分布，ni表示离子密度分布；φ为电势，t为时间；d
z||
和dz⊥
分别是杂质的平行方向与垂直方向的杂质扩散系数；d
e||
和de⊥
分别是电子的平行方向与垂直方向的杂质扩散系数；d
i||
和di⊥
分别是离子的平行方向与垂直方向的杂质扩散系数；和分别是平行方向与垂直方向的梯度算符；s
radz
为杂质的源项，为电子的源项，s
radi
为离子的源项。
[0060]
所述杂质密度分布、电子密度分布和离子密度分布演化方程的具体计算方法如下：
[0061]
步骤4.1：将杂质密度分布、电子密度分布和离子密度分布用谱方法进行表达：
[0062][0063]
其中，(m,n)是环向与极向模数；r0为托卡马克的大半径；θ为极向角；z表示柱向方向；f为粒子分布，包括杂质密度分布、电子密度分布和离子密度分布。
[0064]
步骤4.2：采用两步预测-校正法进行各种粒子分布的时间推进计算。其中，两步预
测-校正法的计算格式如下：
[0065]
预测：
[0066][0067]
校正：
[0068][0069]
其中，h表示磁通量以及磁流体方程中的参数；v为扩散系数；t为时间；代表半个时间步长；dt代表一个时间步长；下标rhs表示磁流体方程的右手项，表示垂直磁场方向的梯度。
[0070]
通过步骤4.1和4.2即可将杂质密度分布、电子密度分布和离子密度分布演化方程求解。之所以采用谱方法和预测-校正法是因为二者可以更加精确、快速且稳定地计算出每一时刻的杂质密度分布、电子密度分布和离子密度分布，进而将杂质密度分布的演化方程、电子密度分布的演化方程、离子密度分布的演化方程与磁流体方程进行耦合，可以自洽地计算出任意时刻的杂质、电子与离子的分布。
[0071]
步骤5：根据步骤4计算出杂质密度分布，当托卡马克芯部的杂质密度分布达到设定的阈值时(该阈值需要根据具体研究是情况确定，例如nz＝1
×
10-5
ne)，进而将等离子体辐射的计算模块打开，从而计算磁场位形随时间的演化并得到此时刻的等离子体总辐射具体步骤如下：
[0072]
步骤5.1：根据电子温度分布te的数值和产生的杂质种类计算出相对应的辐射冷却率l(te)的数值。
[0073]
步骤5.2：计算等离子体总辐射，包括连续性辐射和线辐射。
[0074]
根据连续性辐射公式：
[0075][0076]
和电子回旋辐射公式：
[0077]
pc＝5.4
×
10-25
neb2t
e erg s-1
cm-3
[0078]
以及特征线辐射的计算公式：
[0079]
pz＝nenz∑l(te)erg s-1
cm-3
[0080]
计算出三种辐射的大小，然后将三种辐射累加即可以得到等离子总辐射其中，pb表示连续性辐射的大小，pc表示电子回旋辐射的大小，pz表示线辐射的大小，z
eff
为有效电荷分布。
[0081]
步骤6：将计算出的等离子体总辐射耦合进磁流体方程中，计算一个单位时间步长下的磁通量的演化，并得到加入等离子体总辐射演化后的磁通量
[0082]
步骤7：将步骤5中计算得到的等离子体总辐射的三维空间分布信息输出。
[0083]
步骤8：根据步骤6中计算后得到的考虑等离子体总辐射后的磁通量进一步计算出当下的磁场位形，进而继续重复步骤5-8即得到任意时刻的等离子体总辐射以及考虑等离子体总辐射后的磁通量
[0084]
以上内容是本发明针对先进磁场位形下托卡马克中多种等离子体辐射的数值模拟计算的一个实例的详细说明，不能认定发明的具体实施仅限于这些说明。对本发明所属技术领域的普通技术人员来说，在不脱离本发明的构思的前提下，还可以做出简单的推演及替换，都应当视为本发明的保护范围。