一种基于声学响应的材料物理仿真参数无损估计方法

本发明涉及计算机图形学、声学和物理仿真领域，特别是涉及特别是涉及一种基于声学响应的材料物理仿真参数无损估计方法。

背景技术：

1、真实感声学模拟是计算机图形学中较为活跃的研究领域之一。近年来，领域内研究人员提出了一系列方法提升声学仿真系统的计算效率，但在声学仿真的真实感上的研究相对较少。

2、物理仿真参数的设置对声学模拟的真实感具有较大的影响。传统基于拉压加载的有损物理参数测量方法具有较大的局限性：这种方法会对材料试样造成破坏，而且只能测量材料的杨氏模量等弹性信息，不能测量材料内部的摩擦系数。近年来，研究人员提出了基于视觉的的物体分类方法(参见andrew owens,phillip isola,josh mcdermott,antoniotorralba,edward h.adelson,and william t.freeman."visually indicated sounds."in proceedings of the ieee conference on computer vision and patternrecognition,pp.2405-2413.2016.)，后续研究者进一步将物体分类方法扩展为材料的物理参数估计方法。当前基于深度学习的物理参数测量与估计方法可以针对一部分材料的声学参数实现估计，但这一类方法均以物体下落碰撞的过程作为声学仿真参数测量的主要依据。物体碰撞过程变化范围大，易受外界干扰，难以保证参数测量的稳定性、准确性和鲁棒性。

技术实现思路

1、本发明针对现有技术的不足，提供了一种基于声学响应的材料物理仿真参数无损估计方法，能够在不损伤材料试样的情况下，完成对材料声学仿真参数的估计。

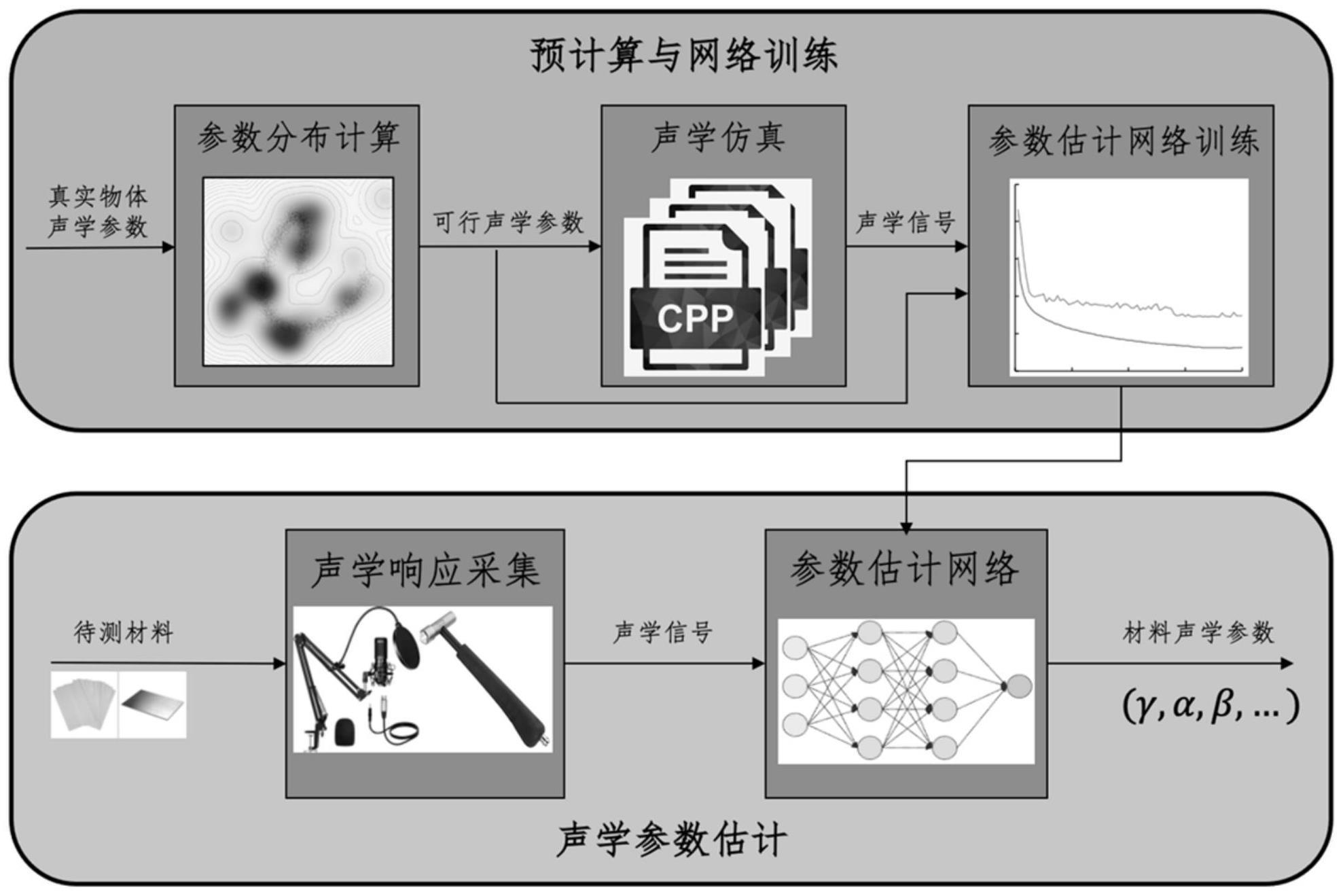
2、为了达到上述目的，本发明采用以下技术方案：一种基于声学响应的材料物理仿真参数无损估计方法，该方法包括以下步骤：

3、(1)对真实世界中材料的声学仿真参数进行采集，包括密度、泊松比和杨氏模量，并且利用高斯混合模型(mixture of gaussian)近似声学仿真参数概率分布，构造仿真参数子空间，从中采样若干组声学仿真参数；

4、(2)采用基于预计算加速的边界元法获得步骤(1)中采样的不同声学仿真参数对应的声学响应信号；

5、(3)将步骤(1)中采样的声学仿真参数和步骤(2)中计算得到的声学响应信号作为训练集，采集工作环境下的n段噪声样本ni(t),i＝1,2,..n，通过短时傅里叶变换，计算时域噪声样本ni(t)的频谱wi；随机选取噪音频谱wi并将它转化为时域信号，和神经网络的输入信号进行叠加完成数据增强，训练一维卷积神经网络，提取声学响应信号中的特征，在一维卷积神经网络输出归一化的同时，将声学仿真参数取对数操作，并建立声学响应信号中的特征和声学仿真参数之间的非线性关系；

6、(4)获得待测材料的冲激声学响应信号，并将该冲激声学响应信号输入到步骤(3)训练得到的神经网络中，得出待测材料的声学响应信号中的特征，从而无损估计出待测材料的物理仿真参数。

7、进一步地，步骤(1)中，声学仿真参数采集时，对于各向异性的材料，将其互异方向上的物理量取为平均值。

8、进一步地，采样若干组声学仿真参数的具体过程如下：

9、(1.1)通过对高斯混合模型进行采样，获得若干近似可行的材料密度、泊松比和杨氏模量；对阻尼参数a和b在进行均匀采样，并和材料密度、泊松比和杨氏模量组合成为完整的若干声学仿真参数；

10、(1.2)分别以低分辨率、次低分辨率网格为载体，快速计算(1.1)中若干声学仿真参数的响应信号，并根据响应信号过滤非法声音仿真参数，从而获取更为合理的若干组声学仿真参数，降低计算成本。

11、进一步地，所述基于预计算加速的边界元法获得不同声学仿真参数对应的声学响应信号的具体步骤如下：

12、(2.1)设置一个薄板作为试验振动的输出结果，并设置空间内麦克风的位置；

13、(2.2)将薄板离散化为n个顶点组成的四面体体网格，给定薄板的密度、杨氏模量、泊松比和阻尼系数，利用neo-hookean本构模型计算材料的质量矩阵m、刚度矩阵k和瑞利阻尼矩阵d＝am+bk，阻尼系数a的范围为[1e-8,1e-5]，阻尼系数b的范围为[0,5e3]，进一步得到材料的动力学方程：

14、

15、其中x为四面体顶点的世界坐标，f为材料所受到的外部冲击；

16、(2.3)通过对质量矩阵和刚度矩阵进行广义特征值分解ku＝mus，并利用特征矩阵u建立特征空间向量q的坐标转换关系x＝uq，计算模态上的振动：

17、

18、通过对模态振动方程进行求解，并对多个模态上的振动进行叠加，计算薄板第i顶点xi的振动函数

19、(2.4)通过固气边界条件，薄板的顶点振动转化为薄板表面声强p(x,t)＝p(x)ejwt，其中w为声波的频率；根据人耳对频率可听范围内的敏度分析，将连续的频率可听范围离散化为若干个频率区间，针对每一频率区间，分别预计算声波在空气中传播所满足的helmholtz方程：

20、

21、其中为拉普拉斯算子，k为波数，p为空间某点处声压。设薄板的几何中心为原点，利用快速多极源法求解helmholtz方程，即可获得若干频率区间上的helmholtz方程数值解；

22、(2.5)根据步骤(2.3)中的模态分析，计算得到当前声学仿真参数对应薄板的若干震动频率，并以该振动频率为依据，从步骤(2.4)中预计算的helmholtz方程数值解中挑选对应数值解进行叠加，从而计算得到空间内麦克风xmic处的声学响应信号p(xmic,t)。

23、本发明的有益效果在于：

24、1.由于本发明是基于材料的声学冲击响应实现材料的物理参数估计的，和传统基于拉压载荷的方法相比，本发明中的技术在仿真参数测量的过程中，不会对材料试样进行破坏，能够无损的对材料属性进行估计；同时，整个参数估计过程可以在3-5s内完成，具有更高的效率。

25、2.和前人研究相比，本发明在采用高斯混合模型对材料的可行物理参数分布进行近似，并通过对该分布进行采样获取可行的声学仿真参数，去除了不合理的密度、杨氏模量和泊松比对，极大地降低了预计算时间。

26、3.和前人研究相比，本发明提出了基于层次化的声学仿真参数过滤方法，去除了不合理的阻尼系数组合，进一步降低了预计算时间。

27、4.本发明提出了一种基于频谱分解的数据增强技术，对工作状态下的室内噪音进行建模，并在网络训练过程中对输入信号进行干预。这使得本发明中的参数估计系统能够稳定的不同室内环境下完成测量任务，具有更强的鲁棒性。

28、5.本发明提出了预计算的边界元法求解目标位置的声音分布。该方法通过对人耳可听范围(20hz-20khz)内进行敏度分析，将连续的可听范围离散化为1000个频率组。通过预计算频率组上的helmholtz方程数值解，提高了边界元法的声音求解速度，降低了声学仿真参数估计的预计算成本。