一种复合材料性能统计分析方法及工程性判断处理系统与流程

本发明涉及复合材料，尤其涉及一种复合材料统计分析方法及工程性判断处理系统。

背景技术：

1、复合材料统计分析中，通常采用复合材料基准值来表现复合材料性能，基准值计算不仅仅是一个数学问题，也是一个工程问题，工程经验与统计上判定都会对结果产生影响。在对已获取的数据组进行分析和检验时，大多数的复合材料试验数据能通过数学统计意义的判定条件，但当有些特殊数据组(即不能通过数学统计意义上的检验条件)出现时，单纯依靠数学统计方法进行判定，容易出现由于数学统计判定条件本身的敏感性而产生误判，造成数据组之间的拆分，影响后续材料基准值的计算精度。在统计意义上的判定中，当数据无法通过异常数据检验、批间变异性检验、拟合优度检验和方差等同性检验四种判定条件时，需要进一步结合工程性判断方法加以分析。专利cn112464484a中虽然列举了异常数据检验、批间变异性检验、拟合优度检验和方差等同性检验相关经验性判定方法，但对于工程设计人员具有很强的主观性，在实际判定过程中人为干预因素过大，会造成数据类型判定失误而导致基准值计算偏差。

2、在鉴定材料基准值计划中，用于检验的材料一般在短期内完成制造，大多数为同一设备制造，实际上并非是多批次的，往往无法获得真实材料性能的变异性。因此，在材料鉴定阶段所度量的变异性通常低于真实的材料变异性，所以需要一种通过对预期的附加变异进行预先考虑的方式对数据进行修正，处理数学统计意义上的判定条件下不能通过的情况。

3、基于工程性方法判断中需要人为经验的主观性判断而导致数据的误判，本发明开发一种适合于工程性判断方法及系统，以数学计算结果为依据，降低人为的经验性干扰因素，进而获得适合于复合材料基准值计算的最佳数据值。

技术实现思路

1、针对上述现有技术的缺点，本发明的目的旨在提供一种复合材料性能数据统计方法，尤其涉及在性能统计分析中的工程性判定。

2、本发明第一方面提供了一种复合材料统计分析方法，该方法包括：

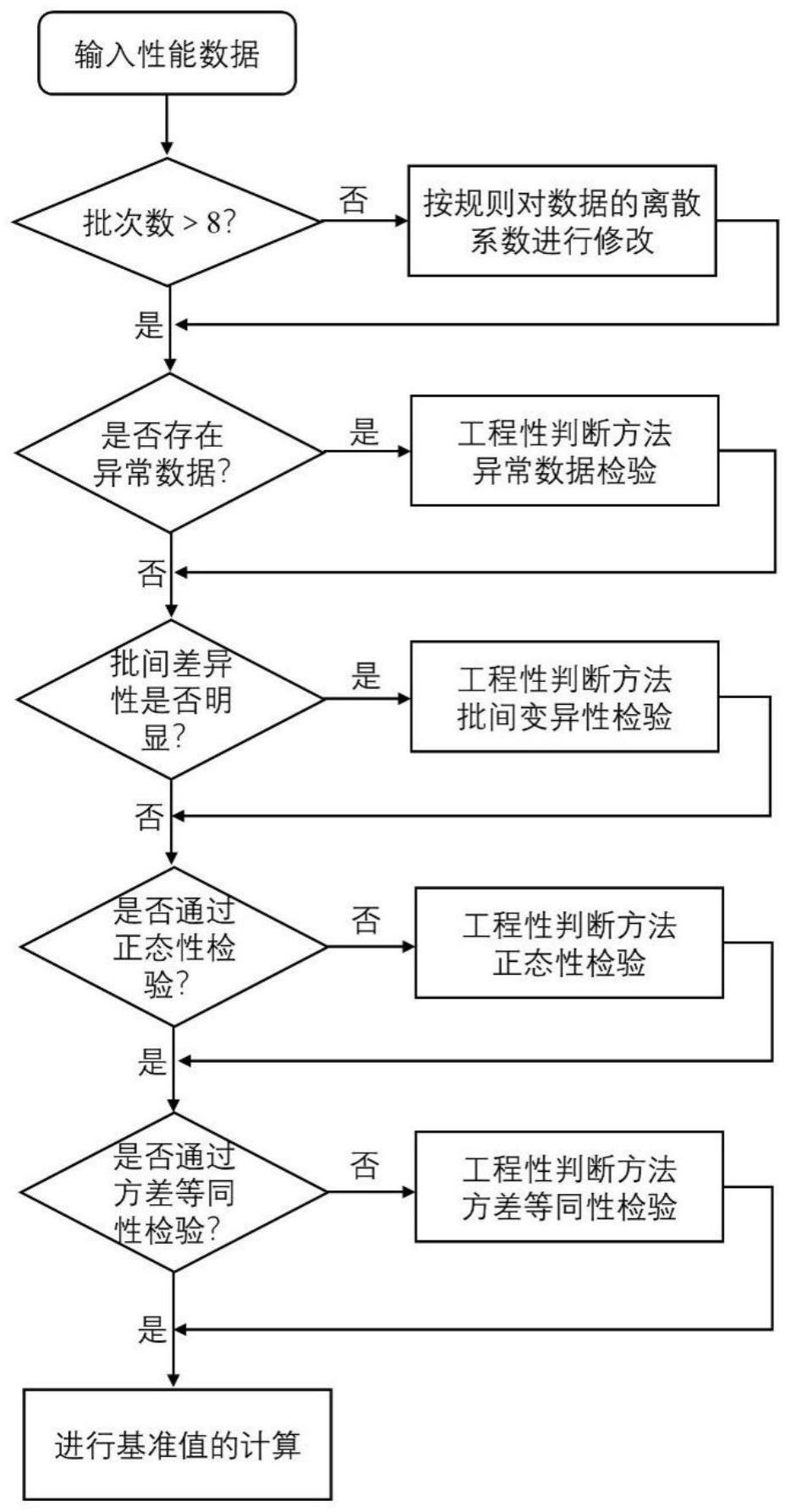
3、s1、通过数学统计方法判断输入的复合材料性能数据，若数据批次数＞8，执行步骤s2；若数据批次数≤8，需要对数据的离散系数进行修正，再执行步骤s2；

4、s2、通过数学统计方法判断输入的复合材料性能数据是否存在异常数据，若判断结果为否，执行步骤s3；若判断结果为是，则通过工程性判断方法进行异常数据检验处理，通过异常数据检验处理后再执行步骤s3；

5、s3、通过数学统计方法判断输入的复合材料性能数据在α＝0.025情况下的批间差异性是否明显，若判断结果为否，即adk＜adc的临界值，则说明样本为同一母体，执行步骤s4；若判断结果为是，即adk≥adc的临界值，则需通过工程性判断方法进行批间变异性检验处理，通过批间变异性检验处理后再执行步骤s4；

6、s4、通过数学统计方法判断输入的复合材料性能数据是否通过正态性检验，若是判断结果为是，执行步骤s5；若判断结果为否，则需通过工程性判断方法进行正态性检验处理，通过检验处理后再执行步骤s5；

7、s5、通过数学统计方法判断输入的复合材料性能数据是否通过方差等同性检验，若判断结果为是，执行步骤s6；若判断结果为否，则需通过工程性判断方法，进行方差等同性检验处理，通过检验处理后执行步骤s6；

8、s6、进行基准值计算。

9、进一步的，在本发明的一个实施例中，对输入数据判断批次数是否满足预设条件(批次数大于8)，当不满足时，需进一步计算各批次数据的离散系数(cv)数值，判断各批次数据的离散系数范围：

10、(1)当cv＜4％，把cv修改为cv*＝6％；

11、(2)当4％≤cv≤8％，把cv修改为cv*＝(0.5×cv)+4％；

12、(3)当cv＞8％，cv保留，不做修改，cv*＝cv。

13、完成修正后，进一步执行后续步骤：检验判定是否存在异常数据。具体的，对不同批次的复合材料数据进行“异常数据检验”，采用最大赋泛残差(mnr法)帮助快速找到异常数据是否满足统计意义上的判定条件，并识别数据结构类型。当试验数据无法通过数学统计判定条件时，数学统计意义上会对数据判定为存在异常数据，则须对异常数据作进一步工程性判定判断处理。具体方法是：采用系统计算输出数据的统计表和统计图，其中统计表的内容包括样本大小、批次数、均值、标准差、离散系数和最值，其中统计图包括不同批次数下复合材料的力学性能测试结果。结合统计表，计算mnr值并于临界值比较，若mnr＜临界值，说明数据正常，执行步骤s3；若mnr＞临界值，说明数据可能异常，需要进一步根据统计图进行判断。结合系统输出的统计图，判断统计表中筛选出的可能异常的数值与其他批次的数据是否在一个范围内，如果可能异常的数值在统计图其他批次数据范围内，则不为异常数据，需要保留，执行步骤s3；若可能异常的数值不在统计图其他批次数据范围内，则说明数据确实为异常数据，需要剔除后，再执行步骤s3。

14、进一步的，在步骤s3中，对数据进行“批间变异性检验”，计算样本数据统计量adk和临界值adc，若adk≥adc，说明不同批次间存在变异性，需进行工程性判断。批间变异性的工程性判断内容有：计算单独批次数据、合并批次数据的离散系数和每批次数据均值。对各值依据以下条件进行判定：

15、条件1：均值接近但方差不同时，如果数据组中95％数据处于各个批次数据的重叠范围内，则认为各批次数据可合并；

16、条件2：各个批次数据的cv都较小，具体地，单层复合材料强度性能离散系数小于4％，层合板和缺口版强度性能离散系数小于3％，合并后数据的cv同样较低，即单层复合材料强度性能离散系数同样小于4％，而层合板和缺口板强度性能离散系数同样小于3％，则认为各批次数据可合并；

17、条件3：各个批次数据合并后，若cv小于试验方法的测量精度(或测量误差)，那么可认为该环境样本的各个批次数据可以合并；

18、条件4：未通过adk检验的环境样本与通过检验的环境样本离散系数相当，可认为该环境样本的各批次数据可合并；

19、条件5：如果某一批次数据的均值始终高于或低于大部分环境样本的均值，则该批次数据不应被合并。

20、当完成上述条件判定，“可合并”数大于“不可合并”数时，即可判定数据可合并，继续执行步骤s4；反之，不能合并，计算终止。

21、进一步地，在本发明的一个实施例中，对所述不同批次的复合材料数据或合并数据进行“正态性检验”，在实际操作中发现，如果严格根据显著性水平(α＝0.05)判断数据的正态性，容易导致大批数据无法通过该检验，影响后续计算精度。所以当数学统计意义上的判定条件无法通过时，利用预设修正策略对数据进行正态性检验的工程性判断和处理。具体的，需要计算降低显著性水平后的osl临界值、计算pearson系数和拟合正态分数曲线图。pearson系数是一种计算直线相关的方法，用于判定数据组r值与临界值的大小，r的绝对值越大，线性相关性越强；正态分数曲线图用于解释复合材料性能数据的正态性。对于给定样本x1,x2,x3,…,xn，anderson-darling统计量为:

22、

23、式中：

24、f0—标准正态分布的累积分函数。

25、

26、上式中：

27、x(i)—样本中第i个最小观测值；

28、—样本的均值；

29、s—样本的标准差。

30、观测显著性水平osl值：

31、

32、

33、若osl＞0.01，则可以断定(1％的错判风险)该样本母体符合正态分布，反之则进行后续计算。

34、pearson(皮尔生)系数r可表示为：

35、

36、式中：

37、—自变量均值；

38、—因变量均值。

39、如果计算出的r值范围为：0.8＜r＜1，则说明该数据组具有很强的线性相关性。

40、正态分数表达式可表示为：

41、

42、xi—数据中的单一数据值；

43、—数据的平均值；

44、σ—数据的标准差。

45、若合并数据正态分数曲线图均落在相对较直的曲线上，则判定样本数据类型具有正态性，继续执行步骤五。反之，计算结束。

46、进一步地，在本发明的一个实施例中，对所述不同批次的复合材料数据或合并数据进行“方差等同性检验”，当数学统计意义上无法通过时，需要利用工程判断方法对数据组进行方差等同性判断处理。主要内容包括分别计算f分布统计值和数据离散系数。具体需要先计算样本的统计值(f计算)，并与α＝0.025时的临界值(f临界(0.025))比较，当f计算<f临界(0.025)，方差等同，执行步骤s6；反之方差不等同，需要进一步与推荐值α＝0.01下的临界值(f临界(0.01))比较，若当f计算<f临界(0.01),则方差等同，执行步骤s6；反之，需要进一步计算各组数据离散系数的差值，如各组离散系数之差均小于10％，则说明数据方差充分等同，执行步骤s6；反之，计算终止。

47、本发明第二方面还提供了一种复合材料性能分析统计中工程性判断处理系统，所述系统包括统计检验模块、工程计算模块和数据输出模块。

48、进一步地，在本发明的一个实施例中，所述统计检验模块，具体用于，对复合材料性能数据中离散系数、异常数据、批间变异性、方差等同性和正态性检验进行统计意义上的检验。

49、进一步地，在本发明的一个实施例中，所述工程判断模块，具体用于：统计检验模块的判断结果做工程计算的进一步判断。

50、进一步地，数据输出模块，用于输出符合条件的数据，输出适合于单点法和多环境样本合并法计算复合材料基准值的最合理的数据类型。

51、本发明的有益效果是：当试验数据未通过数学统计意义上判定条件时，只需通过系统预设的工程性判断方法最终输出变异性小的性能统计数据值，降低现有技术中由于人为因素而引起的主观性判定误差，提高复合材料基准值计算精度。