一种基于物理信息网络的材料参数未知薄板挠度估计方法

本发明涉及深度学习和物理神经网络预测领域，尤其是一种基于物理信息网络的材料参数未知薄板挠度估计方法。

背景技术：

1、薄板是工业生产中广泛使用的装配零件，其结构具有质量小可柔化的特点，易受外部条件干扰产生变形。为快速推动以装配为本的工业生产优化进程，使复杂薄壁件的高效、精准装配成为可能，需要对薄板零件的非线性变形进行精准估计。

2、在传统薄板变形估计领域中，常采用数值方法拟合板件的弯曲状态。对于部分简单的薄板变形问题考虑使用数学公式进行求解，通过增加挠度函数的三角级数项等方式提高计算精度，增补和修正临界应力k值，或是从弹性薄板理论出发，给出非均布表面应力作用下薄板变形问题的挠曲控制方程及相应边界条件，与薄板热应力问题进行物理比拟给出求解，尤其是对简支矩形薄板受纯剪切的失稳问题进行了比较详尽的分析求解。由于该类数学方法使用范围非常有限，导致模型可利用率低，后面的研究尝试通过有限元软件对薄板进行静力及振动模态分析，利用block lanczos法获得薄板的固有频率和对应的振形，以增加少量的空间复杂度为代价，显著减少时间复杂度，并且从加工工艺、刀具的选择、工装夹具设计、切削参数的选取等方面进行考虑，解决了薄板的平面度加工问题。但有限元方法对初始数据高度依赖，难以对数据干扰做出判断和反应，无法达到高端装配制造所需标准。

3、与传统预测方法相比，神经网络适配性强、计算效率高且占用资源少，有较好的抗干扰能力，将边界条件以罚函数法的方式使约束最优化问题转化为求解无约束最优化问题，通过物理模型和初始条件约束的引入，提升了神经网络模型在小训练样本、数据稀疏、噪声情况下的预测的精度和可靠性。目前物理-信息机器学习研究尚处于萌芽阶段，所采用的机器学习模型相对简单，多用于参数估计或模型求解的单向问题，对于应用在实际工程中的复杂薄板变形估计仍需要可靠性高和适用性强的新方法。

4、因此，有必要研发一种基于物理信息网络的材料参数未知薄板挠度估计方法。

技术实现思路

1、本发明需要解决的技术问题是提供一种基于物理信息网络的材料参数未知薄板挠度估计方法，在原来单向训练结构的基础上补全网络模型实现未知材料参数薄板的参数预测和挠度估计，能够避免数据点网格处理后引起的锯齿化和马赛克现象；可靠性更强，适用范围更广的双物理信息网络预测方法，提高网络对干扰的处理能力和对输入信息的提取分析能力，进而降低网络输出与真实变形的偏差程度。

2、为解决上述技术问题，本发明所采用的技术方案是：

3、一种基于物理信息网络的材料参数未知薄板挠度估计方法，包括以下步骤：

4、步骤1，随机测量薄板范围域内点的横向变形数据组成测量点集；

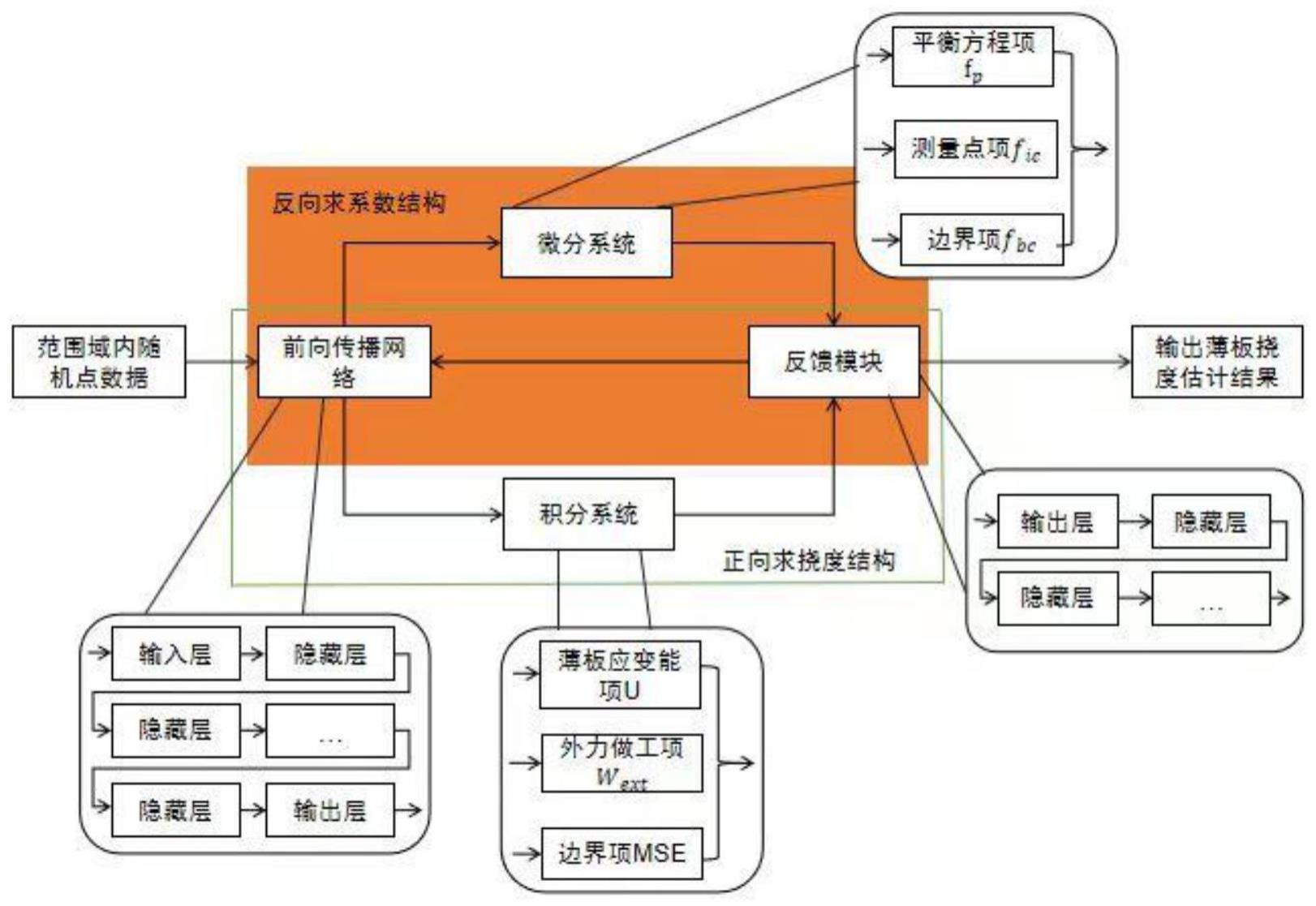
5、步骤2，将步骤1中获取的测量点信息当作双物理信息网络的训练参考项之一，提取范围域内一定数量的随机点坐标作为前向传播网络的输入数据；所述双物理信息网络包含前向传播网络模块、微分系统模块、积分系统模块和反馈模块；

6、步骤3，选择前向传播网络作为薄板变形的替代，将随机点坐标数据输入前向传播网络后，前向传播网络对输入进行线性及非线性递归变换，把前向传播网络的初步训练结果传入微分系统；

7、步骤4，通过材料参数变量初始值和前向传播网络的初步输出计算微分系统误差，使预测结果满足薄板平衡方程和边界条件所施加的物理条件；

8、步骤5，反馈模块根据步骤4中的系统误差逆向传递，完成前向传播网络各层权重偏差反向更新过程；反馈过程为：反向传播利用链式求导法则进行反向计算，若当前输出的误差较大则对损失函数梯度反方向的各个神经元处的权重和偏置值进行调整使新的输出更接近预期值；

9、步骤6，重复训练反馈的过程，不断进行数据计算和信息交换，最终得到满足误差原则的材料参数最佳匹配值；

10、步骤7，引入步骤6得到的材料变量值演算积分系统罚函数，使挠度估计过程在满足最小势能原理的状态下进行；

11、步骤8，将积分系统罚函数传入反馈模块和前向传播网络模块中不断传递迭代，使薄板系统总势能满足边界约束时的最小化，得到薄板挠度估计值。

12、本发明技术方案的进一步改进在于：步骤3中，前向传播网络模块为：

13、定义l层神经网络，第n层有n个神经元定义权重矩阵w和偏差向量b，给定一个非线性激活函数σ，将非线性激活函数σ以元素方式应用，最终实现fnn递归运算，得出神经网络输出结果：

14、输入层：n0(x)＝x

15、隐藏层：nl(x)＝σ(wlnl-1(x)+bl)1≤l≤l-1

16、输出层：nl(x)＝wlnl-1(x)+bl。

17、本发明技术方案的进一步改进在于：步骤4中，所述微分系统误差包含薄板平衡方程误差fp、边界误差fbc和测量点误差fic三部分，表达式如下：

18、f＝fp+fbc+fic

19、薄板小挠度弯曲理论中，薄板弯曲的挠度预测需要满足挠曲面微分方程：

20、

21、由此得到：

22、

23、其中，是弯曲刚度，p为载荷函数，ω为基础场变量，e和v分别表示杨氏模量和泊松比，h是实验弹性薄板的厚度；

24、根据前向传播网络训练得出挠度观测值，由此得到薄板平衡方程误差fp和测量点误差fic：

25、

26、

27、其中，d0′是由训练中得出的弹性模量参数值λ计算出的对应弯曲刚度值，wic是随机测量点变形测量值，是对应点网络训练结果；

28、薄板弯曲问题有三种典型边界条件：

29、(1)几何边界条件γ1：又称固定边界，在边界上给定边界挠度ω′和边界法向斜率

30、(2)混合边界条件γ2：又称简支边界，在边界处给出挠度ω′和法向弯矩mn′；

31、(3)面力边界条件γ3：又称自由边界，在边界处给定横向剪力和法向弯矩mn′；

32、其中，n和s分别对应于沿边界的法线方向和切线方向，边界误差定义为：

33、

34、fb′c为初始边界设定参数值，为网络计算得到的对应边界参数值；

35、通过自动差分方法实现微分系统误差函数计算，自动差分能够通过一次向前传递和一次向后传递计算所有的偏导数，应用自动差分重复使用链式规则得到前向传播网络中输出相对于输入的导数，进行偏微分误差函数拟合。

36、本发明技术方案的进一步改进在于：步骤7中，所述积分系统罚函数分为薄板系统总势能和边界约束罚函数；所述薄板系统总势能π包括薄板应变能u和外力做功wext，表达式如下：

37、π＝u+wext

38、

39、

40、得到薄板系统总势能的积分式后，蒙卡洛特积分通过积分点处的函数密度加权和来实现罚函数计算，通过均方误差法学习边界条件使边界约束下薄板系统总势能最小化：

41、

42、薄板应变能转化为：

43、

44、外力做功转化为：

45、

46、其中，a是薄板范围域的面积，nω是薄板范围域内随机采样点的个数，(xi，yi)是采样点的坐标，u(x，y)是薄板应变能密度函数，f(x，y)是薄板外力做功的密度函数；

47、边界约束罚函数为：

48、

49、

50、γω＝γ1∪γ2，分别为两组边界上随机采样点的个数。

51、由于采用了上述技术方案，本发明取得的技术进步是：

52、1、本发明构建包含前向传播网络模块、微分系统模块、积分系统模块和反馈模块的双物理信息网络，通过微分系统和积分系统实现薄板正反问题拟合，通过增强结构的信息整合分析能力，提高双物理信息网络的预测精度和适用范围，在保证双物理信息网络计算效率和准确度的基础上，完成由采样点到薄板弯曲估计的全过程。

53、2、本发明中构建的双物理信息网络结构完成了从测量点到薄板非线性变形估计的整个过程，工业实用性更强，能够在消耗更少资源的情况下提高网络预测精度和模型效率。