考虑微观接触的栓接结合部分区域虚拟材料建模方法

本发明涉及机械工程，特别是涉及一种考虑微观接触的栓接结合部分区域虚拟材料建模方法。

背景技术：

1、实际中，航空发动机多级转子之间的主要连接形式为螺栓-法兰连接，虚拟材料法通过在零件之间增加一层虚拟材料，将结合部的复杂部件等效为不含结合部的简单零件，实现将复杂的栓接结合部建模简单化的目的，因此被广泛应用于各类型结合部动力学参数化建模中。

2、如现有专利cn114722677a-一种法向和切向载荷耦合作用下栓接结构固有频率的计算方法，引入切向载荷，实现法向载荷和切向载荷耦合作用下的栓接结构固有频率的计算，但是其并未考虑栓接结合部在螺栓预紧力作用下的非均匀接触压力，进而影响了建模精度；现有专利cn107491624b-一种利用虚拟材料等效栓接结合部动态特性的方法，利用多层虚拟材料模拟栓接结合部的动态特性，降低栓接结合部与各子结构间的耦合难度，但是其在确定栓接结合部虚拟材料的参数值时，参数中间值是通过试验测定的，降低了参数的计算效率。

技术实现思路

1、针对上述问题，本发明实施例提供了一种考虑微观接触的栓接结合部分区域虚拟材料建模方法。

2、本发明实施例提供的一种考虑微观接触的栓接结合部分区域虚拟材料建模方法，包括：

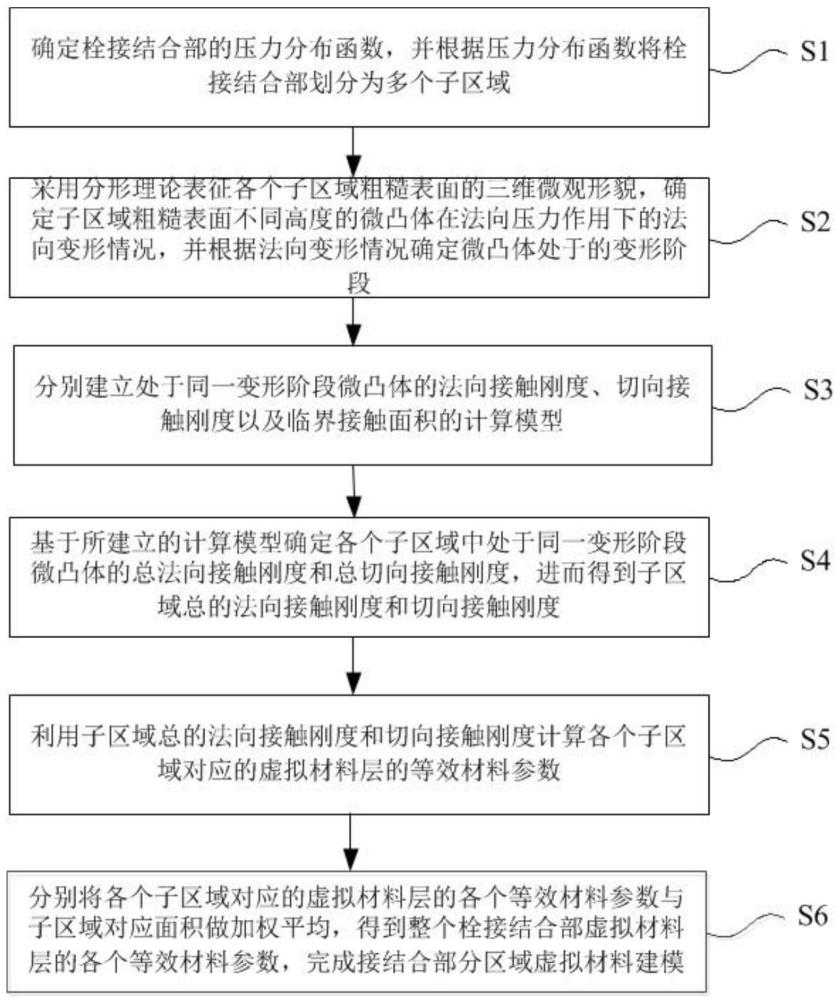
3、确定栓接结合部的压力分布函数，并根据压力分布函数将栓接结合部划分为多个子区域；

4、采用分形理论表征各个子区域粗糙表面的三维微观形貌，确定子区域粗糙表面不同高度的微凸体在法向压力作用下的法向变形情况，并根据法向变形情况确定微凸体处于的变形阶段；

5、分别建立处于同一变形阶段微凸体的法向接触刚度、切向接触刚度以及临界接触面积的计算模型；

6、基于所建立的计算模型确定各个子区域中处于同一变形阶段微凸体的总法向接触刚度和总切向接触刚度，进而得到子区域总的法向接触刚度和切向接触刚度；

7、利用子区域总的法向接触刚度和切向接触刚度计算各个子区域对应的虚拟材料层的等效材料参数；

8、将各个子区域对应的虚拟材料层的等效材料参数与子区域对应面积做加权平均，得到整个栓接结合部虚拟材料层的等效材料参数，完成接结合部分区域虚拟材料建模。

9、可选的，确定栓接结合部的压力分布函数的过程包括：

10、将沿螺栓孔径向方向的栓接结合部法向接触压力等效为四阶多项式函数：

11、p(r)＝a4r4+a3r3+a2r2+a1r+a0 rmin≤r≤rmax                (1)

12、其中，r表示栓接结合部接触区域和螺栓孔中心轴线的距离，ai(i＝0,1...4)表示多项式的常量系数，rmin表示螺栓孔的半径，rmax表示螺栓孔中心线到应力场边界的距离，可以通过式(2)计算式得到：

13、

14、其中，db表示螺栓头的直径，h0表示被连接件的厚度，锥形角αbp反映了栓接结合部应力场区域的大小，且仅与被连接件的结构尺寸有关，由式(3)确定

15、

16、栓接结合部的压力分布需满足以下边界条件：

17、p(rmax)＝0,p′(rmin)＝0,p′(rmax)＝0,p″(rmax)＝0         (4)

18、将边界条件式(4)带入式(1)推导得到：

19、

20、此外，螺栓预紧力fb和栓接结合部法向接触压力p(r)之间满足式(6)：

21、

22、利用式(5)和式(6)计算得到各多项式系数并带入式(1)即可得到栓接结合部的压力分布函数。

23、可选的，采用分形理论表征各个子区域粗糙表面的三维微观形貌的过程包括：

24、粗糙表面由不同尺度的微凸体累加而成，改进的w-m分形函数能够精确的表征三维分形粗糙表面：

25、

26、

27、其中，z(x,y)表示粗糙表面轮廓曲线的高度，x和y表示采样点的坐标值，d表示分形维数反映了表面轮廓在尺度上的不规则性，g表示分形粗糙度反映了粗糙表面轮廓高度大小的特征尺度参数，l表示表面轮廓的采样长度，m表示叠加脊的数量，γ表示随机轮廓的空间频率，φm,n表示随机指数，频率指数n的上限可以表示为：

28、nmax＝int[log(l/ls)/logγ]                          (8)

29、其中，ls表示截止长度。

30、可选的，确定子区域粗糙表面不同高度的微凸体在法向压力作用下的法向变形情况的过程包括：

31、单个微凸体的法向变形量可以表示为：

32、

33、其中，a'表示刚性平面所截得的单个微凸体截面面积；

34、微凸体顶端的等效曲率半径为：

35、r2＝r'2+(r-ω)2                             (10)

36、通常情况下，等效曲率半径r的数量级比法向变形量的高，因此式(10)简化为：

37、

38、因此，微凸体的等效曲率半径可以表示为：

39、

40、由得到的法向变形量和等效曲率半径表征微凸体的法向变形情况。

41、可选的，变形阶段包括纯弹性变形阶段、弹塑性变形阶段和纯塑性变形阶段，且弹塑性变形阶段分为弹塑性第一阶段和弹塑性第二阶段。

42、可选的，建立处于同一变形阶段微凸体的法向接触刚度、切向接触刚度的计算模型包括：

43、纯弹性变形阶段

44、当微凸体受到法向压力较小时，其变形处于弹性范围，根据赫兹接触理论，在纯弹性变形阶段的过程中，单个微凸体的法向接触载荷为：

45、

46、其中，e*表示微凸体的等效弹性模量，计算公式如下：

47、

48、其中，e1和e2分别表示两个被连接件的弹性模量，ν1和ν2分别表示对应的泊松比；

49、将式(9)和式(10)带入式(13)，得到微凸体法向接触载荷的表达式：

50、

51、微凸体的法向接触刚度反应了抵抗弹性变形的能力，可通过下式计算：

52、

53、单个微凸体法向接触刚度与切向接触刚度之间的数学关系如下：

54、

55、弹塑性变形阶段

56、随着微凸体所受的法向压力逐渐增大，微凸体将进入弹塑性变形阶段，且此阶段进一步分为弹塑性第一阶段和弹塑性第二阶段；

57、弹塑性第一阶段的接触荷载为：

58、

59、弹塑性第二阶段的接触荷载为：

60、

61、其中，ωec表示微凸体开始产生塑性屈服时的临界变形，由下式计算得到：

62、

63、其中，h表示材料的硬度，计算公式如下：

64、h＝2.8ss                                (21)

65、其中，ss表示材料的屈服强度；硬度系数k表示为材料泊松比ν的函数：

66、k＝0.454+0.41ν                          (22)

67、相应的，弹塑性第一阶段和弹塑性第二阶段的微凸体的法向接触刚度分别计算如下：

68、

69、

70、弹塑性第一阶段和弹塑性第二阶段的微凸体的切向接触刚度计算如下：

71、

72、

73、纯塑性变形阶段

74、当微凸体的法向变形量不断增加，最终微凸体将处于纯塑性变形阶段，此时法向接触载荷表示为：

75、fp(a')＝ha'＝2hπrω                          (27)

76、处于纯塑性变形阶段的微凸体不存在弹性变形，因此法向接触刚度和切向接触刚度均为零。

77、可选的，建立处于同一变形阶段微凸体的临界接触面积的计算模型包括：

78、根据分形接触理论，a'的分布函数为：

79、

80、其中，a'l表示最大微凸体截断面积，其数值可以表示为子区域实际接触面积ar的函数：

81、

82、子区域实际接触面积ar与其名义接触面积an之比即为无量纲接触面积ad，无量纲接触面积ad通过半解析接触算法进行计算；

83、微凸体在纯弹性变形阶段和弹塑性变形阶段的临界变形量可由式(20)计算，纯弹性变形阶段和弹塑性变形阶段的临界接触面积计算如下：

84、

85、弹塑性第一阶段和弹塑性第二阶段的微凸体临界变形量为：

86、

87、弹塑性第一阶段和弹塑性第二阶段的临界接触面积为：

88、

89、弹塑性变形阶段和纯塑性变形阶段的微凸体临界变形量计算如下：

90、

91、弹塑性变形阶段和纯塑性变形阶段的临界接触面积为：

92、

93、可选的，基于所建立的计算模型确定各个子区域中处于同一变形阶段微凸体的总法向接触刚度和总切向接触刚度，进而得到子区域总的法向接触刚度和切向接触刚度的过程包括：

94、由式(16)和式(28)得到子区域中处于纯弹性变形阶段的微凸体的总法向接触刚度：

95、

96、由式(17)和式(28)得到子区域中处于纯弹性变形阶段的微凸体的总切向接触刚度：

97、

98、由式(23)和式(28)得到子区域中处于弹塑性第一阶段的微凸体的总法向接触刚度：

99、

100、由式(25)和式(28)得到子区域中处于弹塑性第一阶段的微凸体的总切向接触刚度：

101、

102、由式(24)和式(28)得到子区域中处于弹塑性第二阶段的微凸体的总法向接触刚度：

103、

104、由式(26)和式(28)得到子区域中处于弹塑性第二阶段的微凸体的总切向接触刚度：

105、

106、处于纯塑性变形阶段的微凸体的总法向接触刚度和总切向接触刚度均为零，因此，子区域总的法向接触刚度计算如下：

107、

108、子区域总的切向接触刚度计算如下：

109、

110、可选的，各个子区域对应的虚拟材料层的各个等效材料参数包括：等效弹性模量、等效切变模量、等效泊松比、等效厚度以及等效密度，分别计算如下：

111、等效弹性模量

112、子区域受到法向压力作用，等效虚拟材料层的法向应变表示为：

113、

114、其中，δn表示法向变形，h表示虚拟材料层的厚度；

115、在子区域中，等效虚拟材料层的法向平均应力表示为：

116、

117、将式(43)和式(44)带入材料弹性变形的定义式中，得到虚拟材料层的法向等效弹性模量ez的表达式：

118、

119、栓接结合部在x轴方向的弹性模量与两接触表面的结合紧密程度以及被连接件材料的弹性模量有关，虚拟材料层沿x轴方向的弹性模量为：

120、ex＝ade*                              (46)

121、将虚拟材料层视为横观各向同性的，因此，ey＝ex；

122、假设栓接结合部总共被划分为n个子区域，根据均匀复合材料弹性模量计算模型，整个栓接结合部的平均弹性模量表达如下：

123、

124、同理，沿x轴和y轴方向的平均弹性模量和通过计算各个子区域的弹性模量与名义接触面积的加权平均值得到；

125、等效切变模量

126、根据材料切变模量的定义，切变模量为施加的切应力τ与对应的切应变γ之比，因此如下等式关系成立：

127、γ≈tanγ＝δt/h                            (48)

128、虚拟材料层的等效切变模量可以表示为：

129、

130、与平均弹性模量的计算方法类似，整个栓接结合部的平均切变模量表达式如下：

131、

132、等效泊松比

133、根据材料泊松比的定义，在x-z平面内沿z方向拉压的泊松比υzx为：

134、

135、其中，εx表示栓接结合部沿轴x方向的横向变形；在子区域受到法向压力作用时，栓接结合部产生的横向变形基本可以忽略，即εx≈0，故υzx≈0；由于将等效虚拟材料层视为横观各向同性，所以y-z平面内沿z方向拉压的泊松比υzy与υzx相等，即υzy≈0；

136、同理，在x-y平面内沿x方向拉压的泊松比υxy可以表示为：

137、

138、其中，εy表示栓接结合部沿y轴方向的横向变形，与受到法向压力的作用时类似，在x轴方向压缩力的作用下，栓接结合部沿y轴方向的横向变形基本可以忽略不计，因此υxy≈0；

139、等效厚度

140、将栓接结合部等效虚拟材料层的厚度定义为结合部两被连接件表面相互接触的微凸体层厚度h1和h2之和，金属表面微凸体层厚度在0.5mm附近波动，因此虚拟材料层的厚度可以取为：

141、h＝h1+h2＝0.5+0.5＝1(mm)                   (53)

142、等效密度

143、根据材料密度的定义，虚拟材料层的等效密度ρ是栓接结合部等效质量与等效体积v之比，则虚拟材料层等效密度计算如下：

144、

145、其中，m1和m2分别表示分布在两被连接件接触面上的微凸体层的质量，等效体积v是栓接结合部的体积，ρ1和ρ2分别表示两被连接件的材料密度。

146、与现有技术相比，本发明的有益效果在于：充分考虑了栓接结合部在螺栓预紧力作用下的实际应力分布，建模精度更高，同时配合界面的粗糙表面形貌，实现了栓接结合部动力学建模与有限元分析的衔接集成；通过分形接触理论等对参数进行计算，获取参数的计算效率上更高，为栓接结合部动力学建模提供了一种有效且便捷的方法，同时克服了传统的弹簧-阻尼器建模的繁杂性，且计算精度优于均匀虚拟材料的等效建模方法。