一种材料成分与性能映射的不确定性量化方法

本发明涉及一种材料成分与性能映射的不确定性量化方法，属于材料科学和人工智能的交叉。

背景技术：

1、材料的性能受到其成分、微观结构、加工工艺等多种因素的影响，这些因素相互作用，使得预测材料性能变得极其复杂。传统的材料开发依赖于实验室实验和试错法，这不仅耗时耗力，而且可能无法覆盖所有可能的材料组合。机器学习提供了一种数据驱动的方法来预测材料性能，有望加速材料设计的过程。然而，现有的机器学习模型通常缺乏对预测不确定性的量化，这限制了它们在高风险应用中的可靠性和可信度。高斯过程是一种强大的非参数贝叶斯方法，能够提供关于预测的不确定性估计，非常适合处理具有不确定性的复杂系统，拉普拉斯近似是一种数学方法，用于简化后验分布的计算，拉普拉斯近似能够使得高斯过程在实际应用中更加可行。

2、同时深度学习模型在训练时容易遇到梯度爆炸问题，谱归一化通过限制网络层权重的谱范数，帮助控制梯度的大小。lipschitz约束确保模型的输出不会因为输入的微小变化而剧烈波动，提高了模型的稳定性和泛化能力。残差网络通过其残差学习框架，有效地提取了材料成分的深层次特征。transformer模型通过自注意力机制捕捉序列数据的全局依赖性，为材料性能预测提供了新的视角。

3、总而言之，通过对预测不确定性的分析和评估，我们可以更准确地理解模型预测的可信度，从而指导实验设计和材料发现项目，避免资源的浪费和时间的消耗。本发明介绍了一种材料成分与性能映射的不确定性量化方法，该方法将高斯过程与深度学习框架相结合，通过精细的数据分析来探索材料组成与其特性之间的复杂关系。利用高斯过程对不确定性进行量化，从而在材料性能预测中提供了更高的可靠性和精确度。

技术实现思路

1、本发明要解决的技术问题是提供一种材料成分与性能映射的不确定性量化方法，能够量化预测过程中的不确定性，从而解决上述问题。

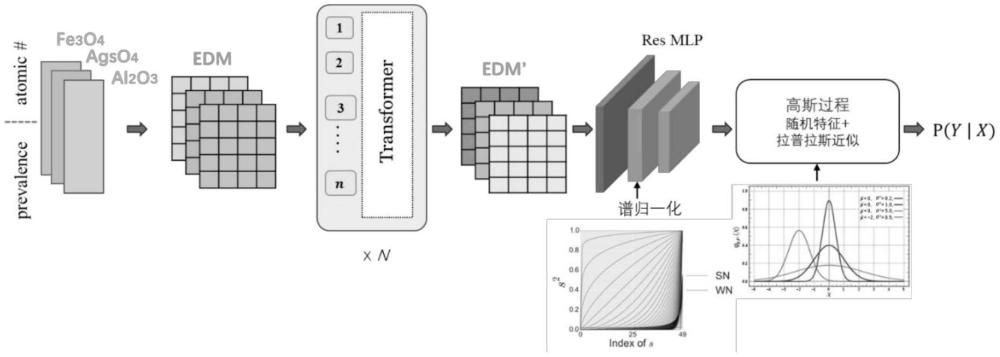
2、本发明的技术方案是：一种材料成分与性能映射的不确定性量化方法，首先，从materials project数据库收集材料成分数据；然后，使用全连接神经网络将数据中的原子序数和分数编码为高维向量；接着，将这些高维向量结合成元素派生矩阵，并输入transformer模块学习化学结构信息，得到化学结构信息特征。最后，化学结构信息特征通过谱归一化残差mlp处理，并在输出层应用高斯过程建模来量化不确定性。

3、具体步骤为：

4、step1：从materials project数据库中收集材料的成分数据，所述成分数据包括每个元素的原子序数和在材料中的分数；

5、step2：使用全连接神经网络将原子序数和分数编码为高维向量，得到元素派生矩阵，所述元素派生矩阵包含了各个元素之间的关系信息；

6、step3：构建transformer模块，将元素派生矩阵输入transformer模块中，通过transformer模块中的自注意力机制，学习材料中各个元素的相互作用以及各个元素的化学结构信息，得到化学结构信息特征；

7、step4：将化学结构信息特征输入到残差多层感知机模块中，在所述残差多层感知机模块中设计谱归一化，约束残差多层感知机模块中权重矩阵的映射，防止过拟合，提高模型的泛化能力；

8、step5：构建高斯模型，通过对数后验似然和hessian矩阵优化高斯模型的参数，然后将残差多层感知机模块中的化学结构信息特征输入到优化后的高斯模型中，进行高斯过程处理，实现量化预测材料成分与性能之间映射的不确定性。

9、所述step2具体为：

10、step2.1：对未进行划分的数据集进行分层随机抽样，固定不同集合中的类别比例，最终抽取为实验所需的训练集、验证集和测试集；

11、step2.2：将每个元素的原子序数通过一个全连接神经网络层，生成对应的高维向量表示，得到元素嵌入矩阵；

12、step2.3：将每个元素的分数通过分数编码生成对应的高维向量表示，得到分数嵌入矩阵；

13、step2.4：将所述元素嵌入矩阵和分数嵌入矩阵结合起来，形成元素派生矩阵，完成对数据集的预处理。

14、所述transformer模块由多个层组成，每层包括自注意力机制和前馈神经网络；

15、在transformer模块中引入两种层间增强机制：残差连接和层归一化；所述残差连接直接将输入添加到经过处理后的输出上；

16、所述层归一化是对每层的输出进行标准化处理，通过标准化特征的均值和方差，使得不同批次的数据都能在相似的尺度上进行训练。

17、所述transformer模块包括3层编码器，每个编码器层内包含4个注意力头，所述注意力头用于捕获输入数据中的上下文信息；

18、编码器的层与层之间的增强机制具体为，每个子层后都包含了残差连接和层归一化：

19、

20、式中，x是输入到这一层的特征向量，维度为rn×d，z(x)是输入x经过前一层处理后的输出，z(x)+x表示残差连接，layernorm表示层归一化，ffn是前馈神经网络，fl是最终输出的编码特征，与x具有相同的维度。

21、所述step4具体为：

22、step4.1：所述残差多层感知机模块由不同的残差块组成，表示为：

23、h＝hl-1·...·h2·h1 (1)

24、hl(fl)＝fl+gl(fl) (2)

25、gl(x)＝a(wlx+bl) (3)

26、式(1)表示整个网络的前向传播过程是由多个层，即从h1到hl-1的组合；

27、式(2)中，fl是进入第l层的输入，gl(fl)是在第l层中对输入fl进行的变换，表示通过这个层后的新特征；

28、式(3)中，wl表示第l层的权重矩阵，用于对输入特征x进行线性变换，a是激活函数，bl是偏置项，gl(x)表示第l层对输入x进行的非线性变换；

29、step4.2：设计谱归一化，将mlp中每一层的权重矩阵进行谱归一化，实现对gl的lipschitz约束；

30、所述谱归一化就是通过幂迭代估计权重矩阵的最大特征值利用最大特征值将权重归一化；

31、

32、式中，c是一个超参数，用于调整权重矩阵谱范数的上界，使得||wl||2≤c，wl是当前第l层的权重矩阵，λ是一个阈值，表示在特定条件下用来比较的标量值。

33、所述高斯过程处理具体为：

34、配备rbf核的高斯模型的先验分布是多元正态分布：

35、

36、式中，σ2和l是超参数，gn×1是一个长度为n的随机向量，表示高斯过程的输出，即预测的值，mvn是多元正态分布，0n×1是一个长度为n的零向量，表示多元正态分布的均值为零，kn×n是一个n×n的协方差矩阵，由rbf核函数生成，表示任意两个观测点之间的相关性，ki,j表示协方差矩阵中的第i行第j列的元素，描述了第i个和第j个输入点之间的相似性，表示第i个和第j个输入点之间的欧几里得距离的平方，l是rbf核的长度尺度使用随机特征扩展来近似先验，定义核矩阵k＝φφt，随机特征高斯过程为：

37、

38、式中，gn×1是一个长度为n的随机向量，表示高斯过程的输出，即预测的值；mvn是多元正态分布；0n×1是一个长度为n的零向量，表示多元正态分布的均值为零；是由随机特征矩阵φ计算得到，其中φ是一个n×dl的矩阵，表示通过随机特征方法生成的特征映射；φi表示残差网络的最后一层，维度为dl，wl是固定的权重矩阵，从n(0，1)中独立同分布采样得到，bl是固定偏置项；

39、使用高斯先验的随机特征扩展来编写由固定隐藏权重wl和可学习输出权重β组成的神经网络层：

40、

41、式中，fo是输入特征向量，g(fo)是神经网络层的输出，基于输入特征fo计算得到；是一个缩放因子，cos(-wlfo+bl)是输入特征fo经过线性变换后的非线性映射，bl是偏置向量，β符合均值为零、方差为τ的多元正态分布，是大小为dl×dl的单位矩阵。

42、所述对数后验似然具体为：

43、

44、式中，logp(β|x)表示参数β在给定输入数据x时的对数后验概率，是关于似然函数的项，用来衡量模型预测值gi与真实值yi之间的差异，是正则化项，称为l2正则化。

45、所述hessian矩阵具体为

46、

47、式中，是一个dl×dl维的hessian矩阵的估计值，φi是一个特征向量，它是在随机特征扩展或神经网络层中生成的；这个项表示特征向量φi的外积，生成一个dl×dl的矩阵，是一个dl×dl的单位矩阵。

48、本发明的有益效果是：

49、1、与现有的不确定性量化方法，本发明提供更准确的材料性能预测的同时，能够生成更可靠的不确定性估计。

50、2、本发明不需要维护大量的模型参数，简化了模型的复杂性。即使在小数据集中，本发明模型也表现出具有竞争力的性能，而在资源允许的条件下，与深度集成方法结合，能产生更准确的材料性能预测以及高质量的不确定性估计。