一种弧形闸门三叉斜支臂扭角的验算求证方法与流程

本发明属于水电站工程技术领域，涉及一种弧形闸门三叉斜支臂扭角的验算求证方法。

背景技术：

弧形闸门由门叶、支臂、支铰(包括铰链、铰轴、铰座等)和止水装置四部分组成。支臂的主要作用是：连接门叶与支铰，将门叶面板承受的水压力传递到支铰，以及铰座安装的水工建筑物之上。常见的斜支臂由上、下两根支柱组成，支柱之间间隔布置竖向支撑和斜向拉杆，将上下支臂连接成一个整体，简称v型支臂。弧形闸门的斜支臂，为保证支臂的支柱腹板与门叶主梁腹板安装后处于同一个平面上(即弧形闸门表面与支铰轴线组成的径向平面)，支柱需要扭转一个角度称作扭角(或扭转角)用φ表示。对于常见的v型斜支臂弧形闸门，“斜支臂水平偏斜角a，支臂上、下支臂夹角2θ，与扭转角φ三个角度之间的函数关系”，在《水电工程钢闸门设计规范》nb35055－2015与《水利水电工程钢闸门设计规范》中的6.1.11条款已经明确规定，规定如下：

“6.1.11斜支臂弧形闸门，当支臂与主横梁水平连接时，在支铰处两支臂夹角平分线的垂直剖面上形成扭角2φ。φ应按式(6.1.11)计算：

其中：θ—上下两支臂夹角的一半；

α—斜支臂水平偏斜角度。”

孔口高度较大时，弧形闸门高度随之增高，v型斜支臂结构不能满足受力和稳定性要求，近年出现了采用三根(或者四根)支柱组成的斜支臂用作超大型弧形闸门，由三根支柱组成的斜支臂简称三叉斜支臂。对于弧形闸门三叉及四叉斜支臂三个角度之间的关系，《水利水电工程钢闸门设计规范》sl74－2013和《水电工程钢闸门设计规范》nb35055－2015，均未明确规定。

一些设计和制造单位对于弧形闸门三叉斜支臂的扭角存在较为模糊的认识。例如：洪都拉斯patucaⅲ水电站工程溢洪道14m×22m×21.5m工作闸门，是三叉斜支臂弧形闸门。将中支臂视作斜支臂中心线，上中、中下支臂的夹角分别视作斜支臂两个不同夹角2θ的一半，代入现行《规范》的扭角计算公式计算，得出的上支臂相对于中支臂的扭角为φ1＝1.1598°,下支臂相对于中支臂的扭角φ2＝0.7909°。

但是《规范》的“6.1.11条款计算公式”设定的使用前提条件是“在支铰处两支臂夹角平分线的垂直剖面上形成的扭角2φ”，该弧形闸门中支臂并非处于“两支臂夹角平分线”上，上中、中下支臂的夹角不相等，并不适应规范规定的使用条件。所以，得出的结果必然是错误的。

因此，现在亟待一种专门针对弧形闸门的中支臂不处于两支臂夹角平分线上的三叉斜支臂扭角的验算求证规范，以避免由于上述错误从而造成重大事故的发生。

技术实现要素：

本发明的目的是针对现有技术的不足，以现有数学的基本原理定理为基础，对弧形闸门三叉斜支臂的空间几何形状进行分析，推导求证出该种支臂结构中：水平偏斜角；上、中支臂中线的夹角(包括中、下支臂中线的夹角)；以及在支铰的垂直端面上形成的扭角等，相关角度之间存在的函数关系。为制定规范的相应条款，做出理论的准备与参考。

本发明解决问题的技术方案是：一种弧形闸门三叉斜支臂扭角的验算求证方法，所述验算求证方法的前提条件为：所述弧形闸门三叉斜支臂的结构，当中支臂作为弧形闸门所受水压的合力方向，上支臂、中支臂和下支臂与主横梁水平连接时，以垂直于所述中支臂平面且与所述中支臂中线垂直的面，作为所述斜支臂的后端板与支铰的连接面；

所述三叉斜支臂的构造角度主要有：所述斜支臂的水平偏斜角α；所述上支臂和所述中支臂之间的夹角θ1，所述中支臂和所述下支臂之间的夹角θ2；在所述斜支臂的后端板平面，所述上支臂相对于所述中支臂的扭角φ1，所述下支臂相对于所述中支臂的扭角φ2；以及所述上中支臂的中心连线与所述后端板垂直中线的夹角η1，所述下中支臂的中心连线与所述后端板垂直中线的夹角η2；

1)基本验算公式为：

所述斜支臂的水平偏斜角：

tanα＝(l-l)/2(r-h)(1)；

α—所述斜支臂的水平偏斜角；

l—所述支铰跨距；

r—所述弧形闸门的面板半径；

h—所述面板的外弧到所述斜支臂的前端板距离；

面板弧长与所述斜支臂在侧墙平面投影的夹角：

l1＝θ1′×rπ/180,

l2＝θ2′×rπ/180(2)；

l1、l2—对应面板的圆弧长度；

θ1′、θ2′—所述斜支臂的所述上支臂与所述中支臂、所述中支臂与所述下支臂在所述侧墙平面投影的夹角；

所述斜支臂与所述侧墙平面投影的夹角：

sin(θ1/2)＝sin(θ1′/2)×cosα，sin(θ2/2)＝sin(θ2′/2)×cosα(3)；

2)所述三叉斜支臂扭角的计算公式：

所述上支臂的腹板中线相对于所述中支臂的腹板中线的扭角：

tanφ1＝sinα×tanθ1′(4)；

所述下支臂的腹板中线相对于所述中支臂的腹板中线的扭角：

tanφ2＝sinα×tanθ2′(5)；

3)所述斜支臂的后端板平面，所述上支臂和所述下支臂与所述中支臂的中心连线夹角计算公式：

η1＝arcsin[sinφ1/(tanθ1×tanα)]+φ1－90°(6)；

η2＝arcsin[sinφ2/(tanθ2×tanα)]+φ2－90°(7)。

进一步的，还包括通过三维建模软件建立所述弧形闸门三叉斜支臂的三维模型的步骤。

进一步的，所述三维建模软件采用autodeskinventor。

本发明的有益效果为：首次填补了《水利水电工程钢闸门设计规范》sl74－2013和《水电工程钢闸门设计规范》《以下简称：规范》nb35055－2015针对弧形闸门三叉斜支臂的扭角验算存在的问题和不足，完善了《规范》，为制定相应条款做出理论的准备与参考。避免了由于验算错误而导致的水利水电工程的重大事故的发生，保证了设计的正确性和精确度，以及施工质量。

附图说明

图1为所述弧形闸门三叉斜支臂的结构示意图。

图2为所述弧形闸门三叉斜支臂的局部放大图。

图3为所述弧形闸门三叉斜支臂的主视图。

图4为所述弧形闸门三叉斜支臂的a-a剖面图。

图5为所述弧形闸门三叉斜支臂的b-b剖面图。

图6为所述弧形闸门三叉斜支臂的c-c剖面图。

图7为洪都拉斯弧形闸门三叉斜支臂的剖面图。

图中：1-门叶，2-左侧斜支臂，3-右侧斜支臂，4-主梁，5-上支臂，6-中支臂，7-下支臂，8-边墙侧，9-闸孔侧。

具体实施方式

下面结合说明书附图和具体实施方式，对本发明具体实施方式作进一步的说明。

实施例一

1.所采用的技术手段

以弧形闸门三叉斜支臂的结构形式，绘制出空间立体几何形状，简化成方便求证的数学模型，以数学的基本定理原理计算推导，总结出相关角度的计算公式。

再采用autodeskinventor软件建立弧形闸门三叉斜支臂的三维模型，通过模型在立体空间自然形成的角度加以验证。

2.三叉斜支臂扭角求证

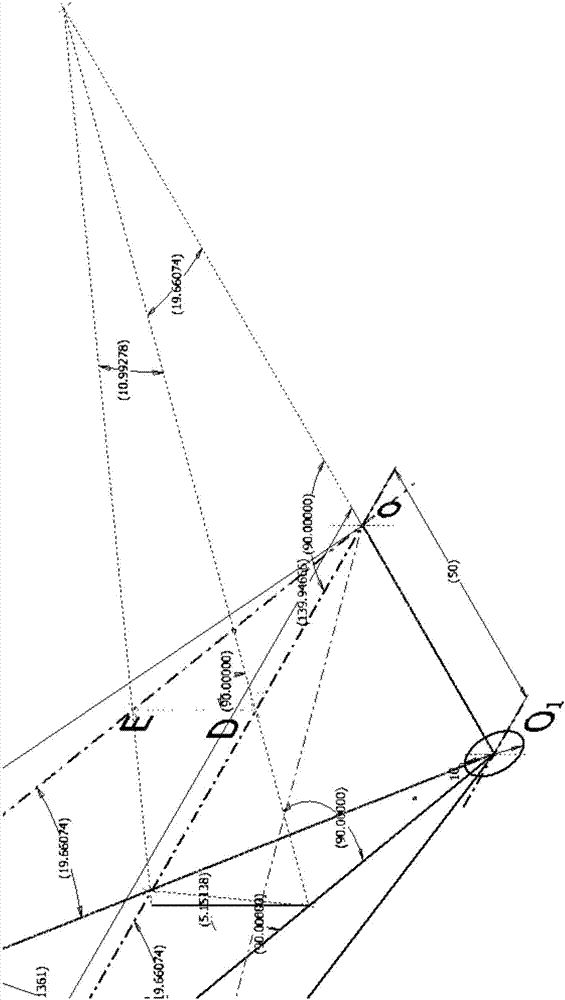
如图1所示，l1、l2分别表示所述上支臂5与所述中支臂6、所述中支臂6与所述下支臂7对应的弧形闸门面板弧长。baco所在平面为过上主梁4、中主梁4、下主梁4与所述斜支臂的前端板中心交点的垂直剖面，所述垂直剖面与侧墙平面、弧形闸门纵向中心面平行。直线bo、ao、co分别是所述上支臂5、所述中支臂6和所述下支臂7中线在垂面的投影，o点为支铰轴线在垂面的中心点。当支臂处于baco平面时，因为与主梁垂直即为直支臂结构形式，bo与ao的夹角θ1′，co与ao的夹角θ2′分别代表所述上支臂5与所述中支臂6、所述中支臂6与所述下支臂7之间的夹角。

推设：位于baco平面的支铰中心点o沿支铰轴线向左侧平移一个距离到达o1点，oo1的距离即为斜支臂的水平偏斜距离，这是直支臂转化为斜支臂的基本道理。此时分别连接b、a、c与o1点的连线，bo1与bo、ao1与ao、co1与co存在一个夹角就是水平偏斜角α，baco1所在的面就是三叉斜支臂所述上支臂5、所述中支臂6、所述下支臂7中线所在的面(需要指出的是bao1与aco1并不处于同一个平面内)。在bao1平面bo1与ao1的夹角θ1，在aco1平面co1与ao1的夹角θ2分别代表斜支臂所述上支臂5与所述中支臂6、所述中支臂6与下支臂7中线之间的夹角。

2.1斜支臂夹角与侧墙平面投影的夹角换算关系

设定式中：l1、l2——为对应面板的弧长；θ1、θ2——为斜支臂所述上支臂5与所述中支臂6、所述中支臂6与所述下支臂7之间的夹角；r——弧形闸门面板圆弧半径；

θ1′、θ2′——为斜支臂所述上支臂5与所述中支臂6、所述中支臂6与所述下支臂7在侧墙平面投影的夹角，或者直支臂所述上支臂5与所述中支臂6、所述中支臂6与所述下支臂7的夹角。

弧长与角度的计算公式如下：

l1＝θ1′×rπ/180,l2＝θ2′×rπ/180

斜支臂夹角与投影夹角的换算公式如下：

sin(θ1/2)＝sin(θ1′/2)×cosα，sin(θ2/2)＝sin(θ2′/2)×cosα

半角公式化为整角公式如下：

cosθ1＝sin²α+cos²α×cosθ1′,cosθ2＝sin²α+cos²α×cosθ2′

2.2斜支臂扭角求证

为方便求证，将中支臂所在的平面aoo1置于水平面，取ao上一个合适的点d，作所述平面的垂线ed，与ao、bo交于d、e点，ed⊥ao；过d点作ao1的垂线交于d点，ed⊥dd；延长d端与oo1的延长线交于f点，df⊥ao1；再以两条直线ed和ddf建立一个平面eddfe，所述平面与中支臂中线垂直即为斜支臂后端板与铰链连接的垂直端面,到中线点o1的距离h设定为铰链的高度；eef与ddf直线形成的夹角φ1即为上支臂平面相对中支臂平面的扭角。

在rt△edf中，tanφ1＝ed/df(1)

在rt△edo中，ed＝tanθ1′×do(2)

因为ao⊥oo1(即o1f)，所以△aoo1为直角三角形，又因为df⊥ao1，所以△o1df、△dof同为为直角三角形，rt△ao1o与rt△o1df共有一个余角，所以∠dfo＝α。

在rt△dof中，df＝do/sinα(3)

将式(2)、(3)代入(1)得：

tanφ1＝sinα×tanθ1′(4)

这即是上支臂相对于中支臂的扭角公式。同理可以得出下支臂的扭角公式：

tanφ2＝sinα×tanθ2′(5)

与所述《规范》的计算公式6.1.11比较之后，得出的结论是，现行规范给出的弧形闸门斜支臂扭角计算公式，只适合于v型斜支臂弧形闸门，不能涵盖三叉斜支臂弧形闸门类型。

2.3支臂后端板平面所述上支臂、所述下支臂与中支臂中心连线夹角的求证

三叉斜支臂上、中、下支臂的三条中线并不在同一个平面内，因此，在后端板平面上三个交点的连线同样不在一条直线上。故理解为：如果将弧形闸门门叶视作车轮轮圈的一部分，支铰视作轮箍的话，所述上支臂、所述中支臂和所述下支臂、所述下支臂中线所在的位置看作斜向外侧的三根辐条。

如图2所示，平面ddfoo1是三叉斜支臂中支臂构成的平面，将其置于水平位置，其中do1是中支臂中线的一部分。平面eddfe垂直于水平面ddfoo1且与do1垂直，相对于o1点的距离用h表示。平移垂面到o1点的距离，当h等于铰链高度加上斜支臂后端板的厚度时，即是斜支臂后端板所在平面。与上支臂中心平面eo1ofe交于eef直线，e为上支臂中线在后端板上的交点。ed连线即是后端板平面上、中支臂截面中心的连线。

在后端板平面内，水平中心线在dd直线上。过d点作df的垂线与eef的延长线交于g点，得到gd直线，即是后端的垂直中心线。下面求证这几个平面构成的角度关系。

在rt△edo1中：ed＝tanθ1×do1(6)

在rt△o1df中：df＝do1/tanα(7)

在△edf中，设∠def＝∠4，∠edf＝∠5，根据正弦定理得：

df/sin∠4＝ed/sinφ1,

将(6)、(7)式代入得：sin∠4＝sinφ1/(tanθ1×tanα)

∠4＝sin^-1[sinφ1/(tanθ1×tanα)]

在△edf中，∠5＝180°-∠4-φ1，∠5即为后端板平面内上中支臂中心连线与后端板水平中线的夹角。

又因为gd⊥df，∠gde＝∠4+φ1－90°，∠gde即为后端板平面内上中支臂中心连线与后端板垂直中线的夹角。设定∠gde＝η1则得出如下表达公式：

η1＝arcsin[sinφ1/(tanθ1×tanα)]+φ1－90°(8)

将公式(8)命名为：后端板平面内，上、中支臂中心连线与后端板垂直中线的夹角公式。同里可以求证出，在后端板平面内：下、中支臂中心连线与后端板垂直中线的夹角公式：

η2＝arcsin[sinφ2/(tanθ2×tanα)]+φ2－90°(9)

上述公式，只是弧形闸门三叉斜支臂扭角计算的一种派生公式。v型斜支臂弧形闸门中，在斜支臂的后端板平面内，上(或下)支柱与平分面投影线中心的连线，相对于斜支臂后端板垂直中线的夹角，与扭角是同一个角度。这也是容易出现设计错误的地方之一。

3.弧形闸门三叉斜支臂扭角的验算方法

通过上述的求证与分析，对弧形闸门三叉斜支臂扭角的验算方法归纳总结如下。

3.1使用的前提条件

如图3～图6所示，弧形闸门采用三叉斜支臂结构布局，当中支臂作为弧形闸门所受水压的合力方向，上、中、下支臂与主横梁水平连接时，以垂直于中支臂平面且与中支臂中线垂直的面，作为斜支臂后端板与支铰的连接面,在此种结构形式下适用。

三叉斜支臂的构造角度主要有：斜支臂水平偏斜角α；上中支臂之间的夹角θ1，中下支臂之间的夹角θ2；在支臂后端板平面，上支臂相对于中支臂的扭角φ1，下支臂相对于中支臂的扭角φ2；以及上中支臂中心连线与后端板垂直中线的夹角η1，下中支臂中心连线与后端板垂直中线的夹角η2。这四种角度之间存在必然的函数关系，使三叉斜支臂结构的相关尺寸与之对应。

设定计算公式中：l1、l2—对应面板的圆弧长度；θ1、θ2—斜支臂上中、中下支臂的夹角；θ1′、θ2′—斜支臂上中、中下支臂在侧墙平面投影的夹角；r—弧形闸门面板半径，h―面板外弧到支臂前端板距离，l―支铰跨距，l―支臂前端板跨距。

以上角度单位：度；

长度、距离单位：毫米。

3.2基本验算公式

斜支臂水平偏斜角计算公式：

tanα＝(l-l)/2(r-h)

面板弧长与斜支臂在侧墙面投影的夹角计算公式:l1＝θ1′×rπ/180,l2＝θ2′×rπ/180

斜支臂与墙侧面投影夹角的换算公式:

sin(θ1/2)＝sin(θ1′/2)×cosα，sin(θ2/2)＝sin(θ2′/2)×cosα

3.3三叉斜支臂扭角计算公式

上支臂腹板中线相对于中支臂腹板中线的扭角公式：tanφ1＝sinα×tanθ1′；

下支臂腹板中线相对于中支臂腹板中线的扭角公式：tanφ2＝sinα×tanθ2′。

3.4支臂后端板平面，上、下支臂与中支臂中心连线夹角计算公式

设定式中：η1——上、中支臂中心连线与后端板垂直中线的夹角，η2——下、中支臂中心连线与后端板垂直中线的夹角，计算公式中其它符号同上。则存在如下函数关系：

η1＝arcsin[sinφ1/(tanθ1×tanα)]+φ1－90°；

η2＝arcsin[sinφ2/(tanθ2×tanα)]+φ2－90°。

该角度是扭角的一种变形，或者说，是同一角度在不同位置的反应。在三叉斜支臂的制作和检测过程中，后者比前者更实用。

4.验证所述验算方法

以洪都拉斯patucaⅲ水电站溢洪道14m×22m×21.5m表孔弧形闸门为例验证。

4.1原图纸设计数据

洪都拉斯patucaⅲ水电站溢洪道14m×22m×21.5m表孔弧形闸门是三叉斜支臂弧形闸门。原图纸设定的斜支臂的水平偏斜角α＝3.9362°，上中支臂的夹角θ1＝15.8036°,中下支臂的夹角θ2＝11.1357°，如图7所示，图纸给出支臂后端板平面上的扭角φ1＝1.1598°,φ2＝0.7909°。

4.2三叉斜支臂扭角公式验算

对此类型弧形闸门框架结构布局进行分析，符合“3.1”条款使用条件，运用总结的公式加以验证。不要局限图纸设定的角度，在弧形闸门结构中，角度只是表示相互位置，因为角度与尺寸单位误差的不同，如果水平偏斜角相差0.001度，该弧形闸门斜支臂前端板跨距就会产生0.88毫米误差，这是安装定位螺栓绝对不允许的。所以，依据基本尺寸对所有角度进行计算，是得出正确结论的前提条件。

l＝12000mm,l＝8537.58mm,h＝1840mm,r＝27000mm,l1＝7465mm,l2＝5260mm。代入“3”条款公式计算得出：α＝3.936205413°(三维软件自动显示科学数据，为了与实测结果一致，尽可能保留多位小数)，θ1′＝15.841222°，θ2′＝11.16206668°。

将计算得出角度参数代入上述推出的三叉斜支臂扭角计算公式：

tanφ1＝sinα×tanθ1′，转化成φ1＝arctan(sinα×tanθ1′)

tanφ2＝sinα×tanθ2′，转化成φ2＝arctan(sinα×tanθ2′)

得出的结果：φ1＝1.115873729°,φ2＝0.776023576°；

继续代入上、下支臂与中支臂中心连线夹角计算公式：

sin(θ1/2)＝sin(θ1′/2)×cosα，转化成θ1＝2arcsin[sin(θ1′/2)×cosα]

η1＝arcsin[sinφ1/(tanθ1×tanα)]+φ1－90°

η2＝arcsin[sinφ2/(tanθ2×tanα)]+φ2－90°

得出的结果：η1＝0.547189252°,η2＝0.384319474°；

4.3三叉斜支臂三维模型自然生成的扭角检测

单凭一个计算结果,不足于认定图纸错误。下面采用autodeskinventor软件建立弧形闸门斜支臂的三维模型，通过模型在立体空间自然形成的角度加以验证。

为了简化视图，模型省略了支柱间连接撑杆，加大了支铰到后端板的距离，省略了斜支臂的裤衩部份，这些改变不会影响角度。三维模型得到的上、下扭角φ1＝1.11587°、φ2＝0.77602°，η1＝0.54719°,η2＝0.38432°与计算结果一致。空间的立体模型验证了三叉斜支臂扭角计算公式的正确性。

4.4三叉斜支臂后端板平面支柱中心连线与后端板垂直中线的夹角的实际应用

在斜支臂的制作过程中，一般的常规工序是：在上、中、下支臂单个零件制作完成之后，进行斜支臂的组拼。

斜支臂的组拼位置，是将斜支臂平置在平台之上，即以支臂后端板的垂直中线所在的面作为水平面。需要首先放出地样：将上、中、下支臂翼板的中线投影到组拼平台(水平面)之上。因为，后端板面支柱中心连线与后端板垂直中线的夹角，等于对应支柱上、下翼板表面的斜角。所以分别以η1、η2的角度制作楔形垫块，以后端板面作为垂面，等距焊接在平台上对应中线位置，作为平台基础基准使用。水平仪配合吊线检测、点焊固定位置配合拉紧器调整，最终保证达到斜支臂扭角的实现。

组拼支臂后端板时，需要先将上、中、下支臂的截面形状以及角度尺寸位置画出在后端板上，并在四周画出找正线，与上、中、下支臂进行组拼焊接。

本发明并不限于上述实施方式，在不背离本发明实质内容的情况下，本领域技术人员可以想到的任何变形、改进、替换均落入本发明的保护范围。