一种管网真实漏失的确定方法及系统与流程

本发明涉及管网漏失领域，特别是涉及一种管网真实漏失的确定方法及系统。

背景技术：

根据《城镇供水管网漏损控制及评定标准》(CJJ92-2016)的规定，管网漏损包含了真实漏失、计量损失、其它损失几个方面。控制管网漏损必须明确以上各组成部分所占的比例，进而有针对性地进行控制。而上述三个组成部分很难定量确定，其中真实漏失是最难以确定的。对管网独立计量区(DMA，district metered area)而言，真实漏失的确定是评价管网健康水平，指导区域检漏及压力控制的重要前提。而目前DMA真实漏失的确定方法较为不准确，为管网健康评价和漏失控制带来了很大的不确定性。

目前有一种DMA真实漏失的确定方法是夜间最小流量(MNF，minimal night flow)分析法。该方法的一种方案是：连续监测DMA入水口的流量，一般固定监测时间间隔为15min，将MNF减去估算的夜间正常用水量得到真实漏失量。其中，夜间正常用水量通常采用经验值估计，比如每户每小时用水2升，用这个值乘以DMA的户数，便可以得到该DMA总的正常夜间用水量。由于夜间正常用水量是估计而来，采用上述技术方案会出现较大的误差；并且由于夜间正常用水是一个随机事件，在15min的监测间隔内，用户发生用水的概率与DMA用户数量是有相关的，而上述方案直接用一个平均值乘以用户数，没有考虑用户数对用水事件发生概率的影响，又会带来一定的误差。这两方面的误差，导致用这种方案计算出来的真实漏失误差较大。

另一种方案是：采用高解析流量计对DMA入水口流量进行连续监测，监测时间间隔一般为几秒，在夜间用水量最小时，可以认为在这几秒的时间间隔内没有用户用水，此时测量得到的MNF就可以认为全部是真实漏失。但是采用高解析流量计的成本较高，采用高解析流量计，监测时间间隔很短，一方面设备的电池消耗太快，需要经常更换；另一方面数据的传输与存储量也很大，会产生相应的高额费用。因此，目前管网真实漏失的确定方法依然存在着高成本、误差大的缺陷。

技术实现要素：

本发明的目的是提供一种管网真实漏失的确定方法及系统，能够在低成本的情况下还能够提高管网真实漏失的测量精度。

为实现上述目的，本发明提供了如下方案：一种管网真实漏失的确定方法，包括：

获取夜间预设时间间隔内单户的平均用水量Q；

根据所述平均用水量计算出单户的平均用水事件数N；

获取独立计量分区内用户数量m；

根据所述用户数量和所述平均用水事件数计算出所述独立计量分区内的平均用水事件数λ；

利用泊松分布计算出在所述独立计量分区内的发生最小夜间流量值的时间间隔内用水事件数为n次的概率值，得到多个概率值；其中，n＝1，2，……2λ-1，2λ；

将所述多个概率值进行比较，计算得到最大概率值；

获取所述最大概率值所对应的n值；

获取独立计量分区入水口的连续7日内的平均最小夜间流量MNF₇；

利用所述平均最小夜间流量MNF₇和所述对应的n值计算得到所述独立计量分区的真实漏失量。

可选的，所述根据所述平均用水量计算出单户的平均用水事件数N，具体包括：

估计单次用水事件的用水量V；

利用公式N＝Q/V计算得到单户的平均用水事件数。

可选的，所述根据所述用户数量和所述平均用水事件数计算出所述独立计量分区内的平均用水事件数λ，具体包括：

利用公式λ＝m×N计算出所述独立计量分区内的平均用水事件数λ。

可选的，所述利用泊松分布计算出在所述独立计量分区内的发生最小夜间流量值的时间间隔内用水事件数为n次的概率值，得到多个概率值，具体包括：

根据概率公式

计算得出发生最小夜间流量值的时间间隔内用水事件数为n次的概率值。

可选的，所述利用所述平均最小夜间流量MNF₇和所述对应的n值计算得到所述独立计量分区的真实漏失量，具体包括：

利用公式RL＝MNF₇-n×V计算得到所述真实漏失量RL。

一种管网真实漏失的确定系统，包括：

平均用水量获取模块，用于获取夜间预设时间间隔内单户的平均用水量Q；

平均用水事件数计算模块，用于根据所述平均用水量计算出单户的平均用水事件数N；

用户数量获取模块，用于获取独立计量分区内用户数量m；

平均用水事件数计算模块，用于根据所述用户数量和所述平均用水事件数计算出所述独立计量分区内的平均用水事件数λ；

概率值计算模块，用于利用泊松分布计算出在所述独立计量分区内的发生最小夜间流量值的时间间隔内用水事件数为n次的概率值，得到多个概率值，其中，n＝1，2，……2λ-1，2λ；

最大概率值计算模块，用于将所述多个概率值进行比较，计算得到最大概率值；

n值获取模块，用于获取所述最大概率值所对应的n值；

平均最小夜间流量获取模块，用于获取独立计量分区入水口的连续7日内的平均最小夜间流量MNF₇；

真实漏失量计算模块，用于利用所述平均最小夜间流量MNF₇和所述对应的n值计算得到所述独立计量分区的真实漏失量。

可选的，所述根据所述平均用水量计算出单户的平均用水事件数N，具体包括：

用水量估计模块，用于估计单次用水事件的用水量V；

单户的平均用水事件数计算模块，用于利用公式N＝Q/V计算得到单户的平均用水事件数。

可选的，所述根据所述用户数量和所述平均用水事件数计算出所述独立计量分区内的平均用水事件数λ，具体包括：

平均用水事件数计算模块，用于利用公式λ＝m×N计算出所述独立计量分区内的平均用水事件数λ。

可选的，所述利用泊松分布计算出在所述独立计量分区内的发生最小夜间流量值的时间间隔内用水事件数为n次的概率值，得到多个概率值，具体包括：

概率值计算模块，根据概率公式

计算得出发生最小夜间流量值的时间间隔内用水事件数为n次的概率值。

可选的，所述利用所述平均最小夜间流量MNF₇和所述对应的n值计算得到所述独立计量分区的真实漏失量，具体包括：

真实漏失量计算模块，用于利用公式RL＝MNF₇-n×V计算得到所述真实漏失量RL。

根据本发明提供的具体实施例，本发明公开了以下技术效果：本发明提出的正常夜间用水的推算方法首先是基于实测的夜间用水数据得来的，其次采用泊松分布反映出用水事件的随机性，比以往基于估计用水量与扣减平均值的方法更加科学、准确，从而提高了管网真实漏失的测量精度；其次，本发明基于DMA入水口流量的变化判断，无需增加额外的监测设备，如高解析水表等，从而大大降低了成本。

附图说明

为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动性的前提下，还可以根据这些附图获得其他的附图。

图1为本发明实施例真实漏失值的确定方法流程图；

图2为本发明实施例真实漏失值的确定系统结构图。

具体实施方式

下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

本发明的目的是提供一种管网真实漏失的确定方法及系统，能够精确监测出管网的真实漏失量，提高检测精度，减少检测误差。

为使本发明的上述目的、特征和优点能够更加明显易懂，下面结合附图和具体实施方式对本发明作进一步详细的说明。

本发明公开一种管网真实漏失的确定方法，图1为本发明实施例真实漏失值的确定方法流程图，如图1所示，该方法包括：

步骤101：获取夜间预设时间间隔内单户的平均用水量Q；

步骤102：根据所述平均用水量计算出单户的平均用水事件数N；

步骤103：获取独立计量分区内用户数量m；

步骤104：根据所述用户数量和所述平均用水事件数计算出所述独立计量分区内的平均用水事件数λ；

步骤105：利用泊松分布计算出在所述独立计量分区内的发生最小夜间流量值的时间间隔内用水事件数为n次的概率值，得到多个概率值；其中，n＝1，2，……2λ-1，2λ；

步骤106：将所述多个概率值进行比较，计算得到最大概率值；

步骤107：获取所述最大概率值所对应的n值；

步骤108：获取独立计量分区入水口的连续7日内的平均最小夜间流量MNF₇；

步骤109：利用所述平均最小夜间流量MNF₇和所述对应的n值计算得到所述独立计量分区的真实漏失量。

在实际应用中，所述根据所述平均用水量计算出单户的平均用水事件数，具体包括：估计单次用水事件的用水量V；利用公式N＝Q/V计算得到单户的平均用水事件数。

在实际应用中，所述根据所述用户数量和所述平均用水事件数计算出所述独立计量分区内的平均用水事件数λ，具体包括：利用公式λ＝m×N计算出所述独立计量分区内的平均用水事件数λ。

在实际应用中，所述利用泊松分布计算出在所述独立计量分区内的发生最小夜间流量值的时间间隔内用水事件数为n次的概率值，得到多个概率值，具体包括：

根据概率公式

计算得出发生最小夜间流量值的时间间隔内用水事件数为n次的概率值。

在实际应用中，所述利用所述平均最小夜间流量MNF₇和所述对应的n值计算得到所述独立计量分区的真实漏失量，具体包括：利用公式RL＝MNF₇-n×V计算得到所述真实漏失量。

将上述步骤应用到实际中，则具体实施步骤如下：

1)选择一定数量的居民用户(以100户以上为宜)，对每个用户2:00am-4:00am间的用水量进行连续监测数日，监测时间间隔以15min为宜，统计所有用户在上述所有监测15min内的单户平均用水量Q；

2)估算单次用水事件的用水量为V，求出在上述15min的监测间隔内，单户平均用水事件数为N＝Q/V；

3)选择某DMA，统计其用户数量，记为m，则在2:00am-4:00am中某一15min的时间间隔内，该DMA的平均用水事件数为m×N个；

4)利用泊松分布模拟在一个DMA内，在2:00am-4:00am中某一15min的时间间隔内发生用水事件数为n次的概率p(X＝n)，公式如下：

式中，p(X＝n)为随机用水事件发生次数为n的概率，λ为2:00am-4:00am中某一15min的时间间隔内随机用水事件发生的平均次数，在本发明中λ＝m×N。

用泊松分布的累积概率计算在2:00am-4:00am中某一15min的时间间隔内发生用水事件数为不大于n次的概率，如下式所示。

式中，F(X≤n)为随机事件发生次数不超过n次的概率。

5)设夜间最小流量MNF发生的15min时间间隔内包含的正常用水事件数为n，可以认为在2:00am-4:00am的其它15min时间间隔内(共7个时间段)，正常用水事件数均不小于n，则其联合概率如下式所示：

式中，X_MNF为最小夜间流量发生的15min时间间隔内随机用水事件发生的次数。

6)令n＝0,1,2,……,2λ-1,2λ,分别求出对应的概率p′(X_MNF＝n)，找出使得概率p′(X_MNF＝n)值最大时对应的n值，记为n₁。当2λ为小数时，四舍五入取整。若有不止一个n值使得p′(X_MNF＝n)同时最大，则将这些n值的平均值作为n₁。

7)用n₁乘以V值，得到该DMA在2:00am-3:00am中某一15min的时间间隔内最可能的正常夜间用水量，记为Q₁；

8)对上述DMA入水口的流量进行连续监测，监测时间间隔固定，以每15min监测一次为宜，提取连续7日的每日最小夜间流量MNF(即每日发生的最小流量，一般发生在2:00am至4:00am之间)，并求7日的平均MNF，记为MNF₇；

9)由MNF₇减去Q₁，得到该DMA的真实漏失量RL。

为了更方便了解本发明的技术方案，我们通过下面的实施例做出进一步解释。

1)在某管网选择了500个居民用户，连续30天监测了每个用户的夜间用水量，统计出平均夜间用水量Q＝0.225L/户/(15min)；

2)由于夜间用水事件通常为冲厕，估计每个马桶的容积V＝6L，则夜间用水事件数N＝Q/V＝0.225/6＝0.0375次/户/(15min)；

3)对某个DMA进行分析，其用户总数m＝1200户，在夜间15min时间内，其平均用水事件数为mN＝1200×0.0375＝45次/(15min)；

4)利用泊松分布模拟在该DMA内，在夜间最小流量MNF发生的15min时间间隔内发生用水事件数为n次的概率p′(X_MNF＝n)，公式如下：

5)令n＝0，1，2，……，89，90，分别求出对应的概率值，经过比较发现，当n＝36时，p′(X_MNF＝36)值最大，则记n₁＝36；

6)由n₁乘以V值，得到在15min时间内最可能的正常夜间用水量

Q₁＝36×6＝216L/(15min)＝0.864m³/h；

7)对该DMA入水口的流量进行连续监测，监测时间间隔固定为15min一次，得到连续7日的平均最小夜间流量MNF₇＝3.5m³/h；

8)计算该DMA的真实漏失量RL＝MNF₇-Q₁＝3.5-0.864＝2.636m³/h。

本发明提出的正常夜间用水的推算方法首先是基于实测的夜间用水数据得来的，其次采用泊松分布反映出用水事件的随机性，比以往基于估计用水量与扣减平均值的方法更加科学、准确。本发明基于DMA入水口流量的变化判断，无需增加额外的监测设备，如高解析水表等，从而大大降低了成本。

另外，DMA一般情况下只有一个入水口。但特别情况下可能会有两个或更多，但每个入水口都需要进行流量监测。在有不止一个入水口的情况下，可将多个入水口的流量先进行叠加(流入为正值，流出为负值)，利用叠加之后的流量进行新增漏失的判断。

其次，最小夜间流量值(MNF)是从若干个夜间流量值中比较得到的，用户夜间正常用水与DMA流量监测的时间段不一定局限于本发明所述的2:00am-4:00am，还可以是其它认为用水较少的时间段；监测时间间隔也不一定是15min，还可以是其它时间间隔，当采用其它时间间隔时，可将公式(4)中的指数“7”更换为其它数值。比如若在2:00am-4:00am之间连续监测，每15min测一个数，则总共有8个数，这8个数中最小的一个就是MNF。此时，t＝8-1＝7。同理，如果每10min测一个数，则总共有12个数，t就等于11，即按照一定时间间隔确定夜间流量值的时间段个数减1就是公式中的t值。

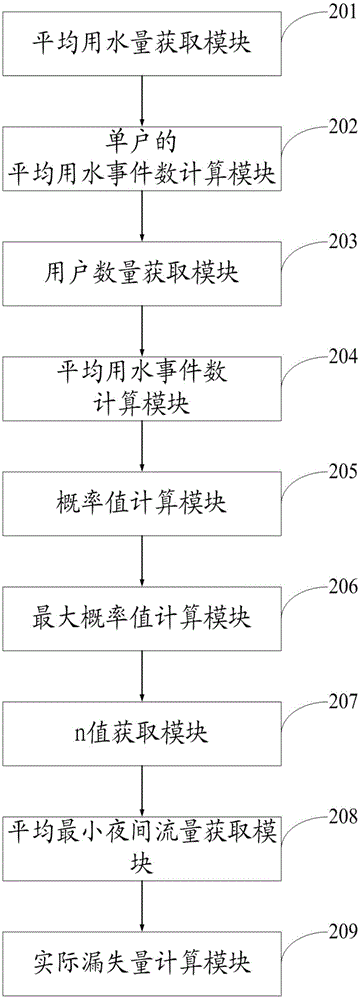
本发明还提出一种管网真实漏失的确定系统，图2为本发明实施例真实漏失值的确定系统结构图，如图2所示，该系统包括：

平均用水量获取模块201，用于获取夜间预设时间间隔内单户的平均用水量Q；

单户的平均用水事件数计算模块202，用于根据所述平均用水量计算出单户的平均用水事件数N；

用户数量获取模块203，用于获取独立计量分区内用户数量m；

平均用水事件数计算模块204，用于根据所述用户数量和所述平均用水事件数计算出所述独立计量分区内的平均用水事件数λ；

概率值计算模块205，用于利用泊松分布计算出在所述独立计量分区内的发生最小夜间流量值的时间间隔内用水事件数为n次的概率值，得到多个概率值；其中，n＝1，2，……2λ-1，2λ；

最大概率值计算模块206，用于将所述多个概率值进行比较，计算得到最大概率值；

n值获取模块207，用于获取所述最大概率值所对应的n值；

平均最小夜间流量获取模块208，用于获取独立计量分区入水口的连续7日内的平均最小夜间流量MNF₇；

真实漏失量计算模块209，用于利用所述平均最小夜间流量MNF₇和所述对应的n值计算得到所述独立计量分区的真实漏失量。

在实际应用中，所述根据所述平均用水量计算出单户的平均用水事件数，具体包括：

用水量估计模块，用于估计单次用水事件的用水量V；

单户的平均用水事件数计算模块，用于利用公式N＝Q/V计算得到单户的平均用水事件数。

在实际应用中，所述根据所述用户数量和所述平均用水事件数计算出所述独立计量分区内的平均用水事件数λ，具体包括：

平均用水事件数计算模块，用于利用公式λ＝m×N计算出所述独立计量分区内的平均用水事件数λ。

在实际应用中，所述利用泊松分布计算出在所述独立计量分区内的发生最小夜间流量值的时间间隔内用水事件数为n次的概率值，得到多个概率值，具体包括：

概率值计算模块，用于根据概率公式

计算得出发生最小夜间流量值的时间间隔内用水事件数为n次的概率值。

在实际应用中，所述利用所述平均最小夜间流量MNF₇和所述对应的n值计算得到所述独立计量分区的真实漏失量，具体包括：

真实漏失量计算模块，用于利用公式RL＝MNF₇-n×V计算得到所述真实漏失量RL。

本说明书中各个实施例采用递进的方式描述，每个实施例重点说明的都是与其他实施例的不同之处，各个实施例之间相同相似部分互相参见即可。对于实施例公开的系统而言，由于其与实施例公开的方法相对应，所以描述的比较简单，相关之处参见方法部分说明即可。

本文中应用了具体个例对本发明的原理及实施方式进行了阐述，以上实施例的说明只是用于帮助理解本发明的方法及其核心思想；同时，对于本领域的一般技术人员，依据本发明的思想，在具体实施方式及应用范围上均会有改变之处。综上所述，本说明书内容不应理解为对本发明的限制。