一种沉管隧道顶进式最终接头位移计算方法与流程

1.本发明涉及沉管隧道监测技术领域，尤其涉及一种沉管隧道顶进式最终接头位移计算方法。


背景技术：

2.沉管隧道最后一节管段的最后一个端面连接之处称为最终接头，用于沉管段与暗埋段之间的最终连接，最终接头是整个沉管隧道中的关键工序之一。最终接头包括外部套筒、顶进节段和顶推系统等，其中外部套筒套设在所述暗埋段的连接端部，顶进节段设置在所述沉管段与所述外部套筒之间，顶进节段的一侧与所述沉管段相固定连接，另一侧与所述外部套筒之间通过后浇筑混凝土连成一体，所述顶推系统用于对所述顶进节段向沉管段一侧顶推滑移。
3.目前，采用顶进节段法施工的沉管隧道最终接头，在对接施工过程中需要实时掌握顶进节段的运动状态，最终确保顶进节段满足线型控制要求。
4.由于沉管隧道最终接头工艺复杂，周期较长，以往监测多为长时间的人工水下探摸，监测安全风险较大，精度相对较差。因此，降低水下作业依赖性，减小监测安全风险，实现顶进式沉管隧道最终接头监测的精准、方便，是沉管隧道顶进式最终接头监测的重要研究方向。中国专利cn202020866287.7公开了一种沉管隧道顶推式最终接头监测结构，该监测结构通过在外部套筒和顶进节段内设置轴向和径向的监测结构，在最终接头的对接施工过程中能够实时掌握顶进节段的运动状态，确保顶进节段满足线型控制要求；并且减小了监测安全风险，最终实现了顶推式沉管隧道最终接头监测的精准和方便。然而对于传感器布置时如何精确计算，该专利没有明确说明，因此在cn202020866287.7的技术基础上进行了进一步的探索。


技术实现要素：

5.本发明为解决公知技术中存在的技术问题而提供一种沉管隧道顶进式最终接头位移计算方法,采用该方法进行沉管隧道顶进式最终接头顶进施工监测，数据质量好，且监测设备结构设计合理、实用性高、稳定性高。
6.为了达到上述目的，本发明采用如下技术方案：
7.一种沉管隧道顶进式最终接头位移计算方法，包括如下步骤：
8.s1、顶进式最终接头移动参数确定；
9.s2、传感器测量系统测量误差分析；
10.s3、传感器测得的监测数据输入筛选；
11.s4、顶进式最终接头运动计算模型；
12.s5、单次计算值冗余筛选；
13.s6、一周期内时间加权数据筛选；
14.s7、局部坐标系转换为施工坐标系；
15.s8、输出控制点坐标值。
16.进一步的，s1中顶进式最终接头移动参数的确定方法如下：
17.最终接头运动模型包括x,y,θxy三个移动参数需要获得；其中x表示最终接头轴向的坐标，y表示最终接头径向坐标，θxy表示最终接头的转角；其中转角值θxy可由纵向传感器差异变化数据计算得到：θxy＝arccos(1-δx2/2l2)；δx为最终接头转角前后的轴向偏差；l为最终接头径向距离。
18.进一步的，s2中测控系统测量误差分析的方法如下：
19.在外部套筒与顶进节段连接区域放点布置传感器支架的安装位置：要求位于顶进节段外侧的传感器尽可能向顶进节段的径向两侧安装，且传感器要沿外部套筒中轴线对称布置，使得θxy以顶进节段的中轴线为转点中心；轴向传感器不少于6个，用于测量监测点的x向位移，径向传感器不少于3个，用于测量监测点的y向位移。轴向传感器量程0～1700mm，按照高精度仪器非线性误差
±
0.05％考虑，相应的轴向传感器测量最大误差为
±
0.85mm；按照该轴向传感器的最大误差，采用两侧轴向传感器的测量误差，要小于采用一侧轴向传感器和中间轴向传感器的测量误差；因此选用两侧管廊轴向传感器作为数据计算点，中管廊轴向传感器数值为校核点。
20.进一步的，s3中传感器的监测数据输入筛选流程如下：
21.步骤1、将传感器监测数据进行数据正负及系数调整；
22.步骤2、由平面几何关系，通过中管廊监测数据判断两侧对称于x轴的轴向传感器监测数据有效性，剔除偏差大于限定误差的数，记录满足差值要求的组合及校验点作为后续计算使用；
23.步骤3、计算得转角α＝arccos(1-δx2/2l2)并修正，δx为最终接头转角前后的轴向偏差；l为最终接头径向距离；
24.步骤4、修正径向位移值；
25.步骤5、判断径向数据有效性，剔除异常数据；记录满足差值要求的组合及校验点作为后续计算使用。
26.进一步的，s4中顶进式最终接头运动计算模型如下：以最终接头顶推前最后标定状态为初始状态，首先计算得传感器头部磁致线圈x、y坐标变化值，然后通过空间几何关系计算得特征点坐标变化值，最后联合标定初始值获得特征点在局部坐标系坐标值，具体的：
27.(1)首先计算某一磁致线圈累计径向变化y”值：
28.y”＝x0*sinθxy+(y0/cosθxy-y0)+y
x0
29.式中：x0，y0为磁致线圈标定坐标值；
30.θxy为顶进节段转角；
31.y
x0
为零点横向变化值；
32.(2)磁致线圈位置在顶进过程中变动模型见以下公式：
33.(l0+x”)2+y”2
＝lx234.式中：l0为传感器上的磁致线圈与磁杆头标定测量值；
35.lx为传感器上的磁致线圈与磁杆头实时距离，即磁杆外露长度；
36.x”为磁致线圈x方向变化值；
37.y”为磁致线圈y方向变化值。
38.对公式进行处理，得到磁致线圈x方向变化值：
39.x”＝(lx
2-y”2
)
0.5-l0；
40.(3)该传感磁致线圈位移后坐标：
41.(x，y)＝(x0+x”，y0+y”)；
42.(4)通过磁致线圈与特征点空间固定关系计算特征点坐标：
43.标定磁杆头初始坐标(x0，y0)，特征点坐标值与标定磁杆头相对坐标差值为(
△
x0，
△
y0)；
44.求得相对坐标夹角γ＝arctan(
△
x0/
△
y0)；
45.则特征点轴向坐标为x＝x0+(
△
x
02
+
△y02
)
0.5
*sin(γ-θxy)；
46.则特征点径向坐标为y＝y0+(
△
x
02
+
△y02
)
0.5
*cos(γ-θxy)；
47.每个有效轴向监测数据可得一批特征点坐标(x，y，z0)。
48.进一步的，s5中单次计算值冗余筛选步骤如下：
49.步骤1、根据轴向传感器有效监测数据，计算得特征点坐标(x，y，z0)取均值为(x
均
，y
均
，z0)；
50.步骤2、若任意特征点坐标与均值坐标差值大于2mm，删除该特征点坐标后进入步骤3；若任意特征点坐标与均值坐标差值均不大于2mm，进入步骤5；
51.步骤3、若剩余特征点不少于2个，进入步骤4；若剩余特征点仅有1个，取特征点坐标为全部坐标，得均值(x
均
，y
均
，z0)；
52.步骤4、重新计算剩余特征点坐标均值，重复步骤2；
53.步骤5、取特征点坐标为剩余特征点坐标均值(x
均
，y
均
，z0)。
54.进一步的，s6中一周期内时间加权数据筛选方法如下：
55.(1)各特征点坐标(x1，y1，z)～(x5，y5，z)按照时间顺序分别乘以对应时间权值11～15后累加取均值为(x
均
，y
均
，z)；
[0056][0057]
(2)若存在任意计算特征点坐标与均值坐标差值大于2mm，删除超限正负极差值；
[0058]
(3)刨除已删除特征点坐标及权值，重新按照上述公式进行计算得该时间内特征点坐标值(x
均
，y
均
，z)。
[0059]
进一步的，s7中局部坐标系转换为施工坐标系方法如下：
[0060]
平面二维转换方法需要4个参数，包括2个平移、1个旋转、和1个尺度。坐标系xo-yo经过尺度缩放，坐标系旋转，然后再平移，变成了xt-yt坐标系：
[0061]
xt＝
△
x+k*x0*cos
ɑ-k*y0*sin
ɑ
；
[0062]
yt＝
△
y+k*x0*sin
ɑ
+k*x0*cos
ɑ
；
[0063]
其中：其中本局部坐标系与施工坐标系尺度相同，k均为1；
[0064]
xt表示施工坐标系x轴；
[0065]
△
x表示本局部坐标系原点在施工坐标系x轴的坐标值；
[0066]
xo表示本局部坐标系x轴；
[0067]
yo表示本局部坐标系y轴；
[0068]
yt表示施工坐标系y轴；
[0069]
△
y表示本局部坐标系原点在施工坐标系y轴的坐标值；
[0070]
ɑ
表示本局部坐标系与施工坐标系夹角，可由两坐标系已知坐标值换算来；
[0071][0072]
其中，xoa为局部坐标系中一已知x坐标值；
[0073]
yoa为局部坐标系中一已知y坐标值；
[0074]
xob为局部坐标系中另一已知x坐标值；
[0075]
yob为局部坐标系中另一已知y坐标值；
[0076]
xta为施工坐标系中一已知x坐标值；
[0077]
yta为施工坐标系中一已知y坐标值；
[0078]
xtb为施工坐标系中另一已知x坐标值；
[0079]
ytb为施工坐标系中另一已知y坐标值；
[0080]
最后获得特征点施工坐标系(yt，xt，zt)；高程zt为局部坐标原点的施工坐标系高程和该点局部坐标高之和。
[0081]
进一步的，s7中输出控制点坐标值是指按照要求将特征点坐标值及相应测量值标记时间顺序后存入计算机数据库中，全部原始测量数据测量后均按时间顺序也存入计算机数据库中；根据外界模型或交互设备需要，定时或按需给出计算特征值坐标。
[0082]
本发明具有的优点和积极效果是：
[0083]
1、采用本发明的方法进行监测，监测数据准确稳定，且该监测方法已成功应用于大连湾海底隧道建设工程最终接头模拟顶进施工监测。
[0084]
2、本发明的方法监测数据溯源性高，可为多种计算模型提供数据。
[0085]
3、本发明的方法监测数据稳定向高，避免监测数据不可控。
[0086]
4、本发明适用于满足监测要求多种监测传感器，不仅限于特定厂家型号传感器，具有广谱适用性。
附图说明：
[0087]
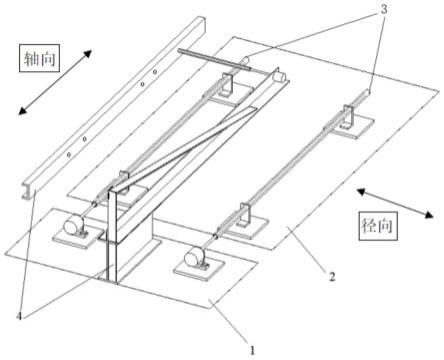
图1是现有技术中最终接头上传感器监测结构的三维布置示意图；
[0088]
图2是顶进节段中传感器的布置示意图以及对应的坐标系；
[0089]
图3是不考虑仪器安装误差，但考虑轴向传感器安装误差的情况下，采用径向两侧的轴向传感器工作时，对顶出节段顶出量及旋转角度测量误差的影响；
[0090]
图4是考虑了仪器安装误差，同时考虑轴向传感器安装误差的情况下，采用径向两侧的轴向传感器工作时，对顶出节段顶出量及旋转角度测量误差的影响；
[0091]
图5是考虑了仪器安装误差，同时考虑轴向传感器安装误差的情况下，采用径向一侧和中间的轴向传感器工作时，对顶出节段顶出量及旋转角度测量误差的影响；
[0092]
图6是本发明的顶进节段旋转示意图；
[0093]
图7是本发明的顶进节段转角对径向监测数据修正计算图；
[0094]
图8是本发明的传感器测得的监测数据筛选流程图；
[0095]
图9是本发明的磁致线圈在顶进过程中的变动模型；
[0096]
图10是本发明的最终接头局部坐标系与施工坐标系的转换示意图。
[0097]
其中：1、外部套筒；2、顶进节段；3、轴向传感器；31、第一轴向传感器；32、第二轴向传感器；33、第三轴向传感器；34、第四轴向传感器；35、第五轴向传感器；36、第六轴向传感器；4、径向传感器；41、第一径向传感器；42、第二径向传感器；43、第三径向传感器；5、中管廊；6、磁止线圈。
具体实施方式
[0098]
下面将结合本发明实施例中的附图；对本发明实施例中的技术方案进行清楚、完整地描述；显然；所描述的实施例仅仅是本发明一部分实施例；而不是全部的实施例。基于本发明中的实施例；本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例；都属于本发明保护的范围。
[0099]
如图1-10所示，本发明提供了一种沉管隧道顶进式最终接头位移计算方法，包括如下步骤：
[0100]
s1、顶进式最终接头移动参数确定
[0101]
如图1所示，顶进式最终接头顶进节段长宽高约为10m*34m*5.8m，净体积占比较大，采用c50混凝土，配筋合理，结构形式简单。顶进施工过程中，受力均匀，不存在发生结构整体扭转，大的变形等情况，可认为最终接头顶进节段为一个刚体。
[0102]
对于确定的刚体，如果设置相应的六个约束，分别用于限制该刚体的六个运动自由度，就可以使该自由刚体在空间有一个确定的位置，该方法称之为六点定位原则。
[0103]
任何一个处于空间直角坐标系中的物体，如果不受其他物体对它的约束，它的位置是不确定的，是“自由”的，共有六种运动可能，称之为六个自由度，即沿直角坐标系x、y、z三轴方向的移动自由度和绕此三轴的转动自由度，顶进节段的顶进完成正确安装，就要求顶进节段在顶进施工过程中保持安全轨迹，并最终到达预设位置，从而实现顶进式最终接头的完成。
[0104]
显然，顶进节段不是完成为处于“自由”状态的刚体。针对现场实际工况对6个自由度进行分析，找到实际限制条件从而限制多余的自由度，从而计算得到较为正确的位置。
[0105]
以外部套筒和顶进节段的中轴线为x正方向，外部套筒和顶进节段的水平径向为y方向，以竖直向上为z正方向。对于z方向，可通过事先对施工过程滑轨表面高程的控制进而控制轨道上的顶进节段的竖向标高。顶进节段滑轨设置为水平，即顶进节段z轴数值不变。顶进节段顶进施工过程平缓，受力较为一致，基础平稳，不会出现倾覆情况，因此z方向绕x、y轴的转角θzx,θzy不会产生转动变化。计算最终接头运动模型仅剩余x,y,θxy三个自由度需要通过现场监测直接或间接获得；其中x表示最终接头轴向的坐标，y表示最终接头径向坐标，θxy表示最终接头的转角；其中转角值可由轴向传感器差异变化数据计算得到：θxy＝arccos(1-δx2/2l2)；δx为最终接头转角前后的轴向偏差；l为最终接头径向距离。
[0106]
s2、传感器测量系统测量误差分析
[0107]
如图2所示，在外部套筒与顶进节段连接区域放点布置传感器支架的安装位置：要求位于顶进节段外侧的传感器尽可能向顶进节段的径向两侧安装，且传感器要沿外部套筒中轴线对称布置，使得θxy以顶进节段的中轴线为转点中心；轴向传感器不少于6个，用于测量监测点的x向位移，径向传感器不少于3个，用于测量监测点的y向位移。本实施例优选轴向传感器为6个，从一侧至另一侧分别命名为第一轴向传感器至第六轴向传感器；径向传感
器为3个，从一侧至另一侧分别命名为第一径向传感器至第三径向传感器；所有轴向传感器量程0～1700mm，按照高精度仪器非线性误差
±
0.05％考虑，相应的轴向传感器测量最大误差为
±
0.85mm；按照该轴向传感器的最大误差，顶进节段轴向顶出量及旋转角度测量误差分析如下：
[0108]
1)图3给出了不考虑仪器安装误差，同时考虑轴向传感器安装误差为0.85mm的情况下，采用径向两侧的轴向传感器工作时，顶进节段最外侧边缘顶出量最大误差为
±
1.07mm，顶进节段的旋转角度最大误差为
±
13.10
″
；
[0109]
2)图4在图3的基础上考虑了仪器安装误差，同时考虑轴向传感器安装误差为0.85mm的情况下，采用径向两侧的轴向传感器工作时，顶进节段最外侧边缘顶出量最大误差为
±
1.08mm，顶进节段的旋转角度最大误差为
±
13.22
″
；
[0110]
3)图5给出了考虑仪器安装误差，同时考虑轴向传感器安装误差为0.85mm的情况下，由其中一侧轴向传感器及中间传感器测量时：顶进节段最外侧边缘顶出量最大误差为
±
3.02mm，顶进节段的旋转角度最大误差为
±
26.56
″
。可见，采用两侧轴向传感器的测量误差，要小于采用一侧轴向传感器和中间轴向传感器的测量误差。
[0111]
顶进节段顶出量及旋转角度测量误差分析：顶进节段的旋转会导致最终接头外部套筒与顶进节段间最小净距的改变。根据图6，最小净距减小量小于ly
×
sinθ，该处的ly为外部套筒的轴向尺寸，取5800mm。据此计算得出图4和图5情况下的外部套筒与顶进节段径向测量误差分别为0.37mm和0.75mm。因此选用两侧管廊轴向传感器作为数据计算点，中管廊轴向传感器数值为校核点。
[0112]
传感器巡测具有时间差，9个传感器巡测时间总间隔不大于0.1s，按照0.2s测量间隔进行测量，每1s获得5组数据。千斤顶顶推速度按40mm/min计算，则每秒千斤顶顶推行程为0.67mm，与测量误差的幅值相当。所以，传感器巡测时间间隔对测试数据无影响。若顶进速度大于40mm/min，可调整1s周期间隔，使得周期前后运动差值满足不大于传感器误差值的2倍。
[0113]
s3、传感器测得的监测数据输入筛选
[0114]
步骤1、将传感器监测数据进行数据正负及系数调整；
[0115]
步骤2、由平面几何关系，通过中管廊监测数据判断两侧对称于x轴的轴向传感器监测数据有效性，剔除偏差大于限定误差的数，记录满足差值要求的组合及校验点作为后续计算使用；
[0116]
步骤3、计算得转角θxy＝arccos(1-δx2/2l2)并修正，δx为最终接头转角前后的轴向偏差；l为最终接头径向距离；
[0117]
顶进节段转角α对径向监测数据的修正计算如图7所示；
[0118]
a.以顶进节段中轴线与径向监测点x坐标相同的点为圆心进行转动，转角为θxy，转角θxy以顺时针为正；x、y距离值以坐标系正向为正；
[0119]
y1为转动后在y轴负方向的变化值，根据几何关系：
[0120]
(y1+y)*cosθxy＝y
[0121]
y为坐标值，θxy经计算得到，易计算得到该点在转动下引起的径向变化y1，即修正系数值为-y1。
[0122]
b.以传感器磁杆头中轴线上某x坐标点为圆心进行转动，转角为θxy，根据几何关
系：
[0123]
y’＝x*sinθxy
[0124]
x为坐标值，θxy经计算得到，易计算得到该点在转动下引起的径向变化y’，即修正系数值为-y1。
[0125]
步骤4、修正径向位移值；
[0126]
步骤5、判断径向数据有效性，剔除异常数据；记录满足差值要求的组合及校验点作为后续计算使用。
[0127]
以上步骤具体筛选流程如图8所示。
[0128]
s4、顶进式最终接头运动计算模型
[0129]
以最终接头顶推前最后标定状态为初始状态。首先计算得传感器头部磁致线圈x、y坐标变化值，然后通过空间几何关系计算得特征点坐标变化值，最后联合标定初始值获得特征点在局部坐标系坐标值，具体的：
[0130]
(1)首先计算某一磁致线圈累计径向变化y”值：
[0131]
y”＝x0*sinθxy+(y0/cosθxy-y0)+y
x0
[0132]
式中：x0，y0为磁致线圈标定坐标值；
[0133]
θxy为顶进节段计算转角；
[0134]yx0
为零点横向变化值；
[0135]
(2)磁致线圈位置在顶进过程中变动模型见图9，根据勾股定理得已下公式：
[0136]
(l0+x”)2+y”2
＝lx2[0137]
式中：l0为传感器上的磁致线圈与磁杆头标定测量值；
[0138]
lx为传感器上的磁致线圈与磁杆头实时距离，即磁杆外露长度；
[0139]
x”为磁致线圈x方向变化值；
[0140]
y”为磁致线圈y方向变化值。
[0141]
对公式进行处理，得到磁致线圈x方向变化值：
[0142]
x”＝(lx
2-y”2
)
0.5-l0；
[0143]
(3)该传感磁致线圈位移后坐标：
[0144]
(x，y)＝(x0+x”，y0+y”)；
[0145]
(4)通过磁致线圈与特征点空间固定关系计算特征点坐标：
[0146]
标定磁杆头初始坐标(x0，y0)，特征点坐标值与标定磁杆头相对坐标差值为(
△
x0，
△
y0)；
[0147]
求得相对坐标夹角γ＝arctan(
△
x0/
△
y0)；
[0148]
则特征点轴向坐标为x＝x0+(
△
x
02
+
△y02
)
0.5
*sin(γ-θxy)；
[0149]
则特征点径向坐标为y＝y0+(
△
x
02
+
△y02
)
0.5
*cos(γ-θxy)；
[0150]
每个有效轴向监测数据可得一批特征点坐标(x，y，z0)。
[0151]
s5、单次计算值冗余筛选
[0152]
(1)根据轴向传感器有效监测数据，计算得特征点坐标(x，y，z0)取均值为(x
均
，y
均
，z0)；
[0153]
(2)若任意特征点坐标与均值坐标差值大于2mm，删除该特征点坐标后进入步骤(3)；若任意特征点坐标与均值坐标差值均不大于2mm，进入步骤(5)；
[0154]
(3)若剩余特征点不少于2个，进入步骤(4)；若剩余特征点仅有1个，取特征点坐标为全部坐标，得均值(x
均
，y
均
，z0)；
[0155]
(4)重新计算剩余特征点坐标均值，重复步骤(2)；
[0156]
(5)取特征点坐标为剩余特征点坐标均值(x
均
，y
均
，z0)。
[0157]
s6、一周期内时间加权数据筛选
[0158]
(1)各特征点坐标(x1，y1，z)～(x5，y5，z)按照时间顺序分别乘以对应时间权值11～15后累加取均值为(x
均
，y
均
，z)；
[0159][0160]
(2)若存在任意计算特征点坐标与均值坐标差值大于2mm，删除超限正负极差值；
[0161]
(3)刨除已删除特征点坐标及权值，重新按照上述公式进行计算得该时间内特征点坐标值(x
均
，y
均
，z)。
[0162]
s7、局部坐标系转换为施工坐标系
[0163]
施工坐标系是施工项目中各项测量的基础和依据，贯穿工程项目从设计、施工及运行中维护各阶段，因此需要将局部坐标系转换成施工坐标系。施工坐标系也是3维空间坐标系，高程一般采用国家85高程系，平面坐标采用2000国家施工坐标系或项目所在地城建坐标系。
[0164]
所谓坐标系转换是在两个不同的坐标系之间建立的数据转换关系。转换关系建立后，两个坐标中的任何一个点的坐标可以在两个坐标系之间进行相互换算。鉴于顶进式最终接头施工期间高程恒定，暂不使用较为繁琐的空间三维(7参数)转换方法，使用平面二维(4参数)转换方法。
[0165]
如图10所示，平面二维转换方法需要4个参数，包括2个平移、1个旋转、和1个尺度。坐标系xo-yo经过尺度缩放，坐标系旋转，然后再平移，变成了xt-yt坐标系：
[0166]
xt＝
△
x+k*x0*cos
ɑ-k*y0*sin
ɑ
；
[0167]
yt＝
△
y+k*x0*sin
ɑ
+k*x0*cos
ɑ
；
[0168]
其中：其中本局部坐标系与施工坐标系尺度相同，k均为1；
[0169]
xt表示施工坐标系x轴；
[0170]
△
x表示本局部坐标系原点在施工坐标系x轴的坐标值；
[0171]
xo表示本局部坐标系x轴；
[0172]
yo表示本局部坐标系y轴；
[0173]
yt表示施工坐标系y轴；
[0174]
△
y表示本局部坐标系原点在施工坐标系y轴的坐标值；
[0175]
ɑ
表示本局部坐标系与施工坐标系夹角，可由两坐标系已知坐标值换算来；
[0176][0177]
其中，xoa为局部坐标系中一已知x坐标值；
[0178]
yoa为局部坐标系中一已知y坐标值；
[0179]
xob为局部坐标系中另一已知x坐标值；
[0180]
yob为局部坐标系中另一已知y坐标值；
[0181]
xta为施工坐标系中一已知x坐标值；
[0182]
yta为施工坐标系中一已知y坐标值；
[0183]
xtb为施工坐标系中另一已知x坐标值；
[0184]
ytb为施工坐标系中另一已知y坐标值；
[0185]
最后获得特征点施工坐标系(yt，xt，zt)；高程zt为局部坐标原点的施工坐标系高程和该点局部坐标高之和。
[0186]
s8、输出控制点坐标值
[0187]
s7中输出控制点坐标值是指按照要求将特征点坐标值及相应测量值标记时间顺序后存入计算机数据库中，全部原始测量数据测量后均按时间顺序也存入计算机数据库中；根据外界模型或交互设备需要，定时或按需给出计算特征值坐标。
[0188]
某次顶推试验该模型计算数据与全站仪计算差值见表1，全站仪取2台测量均值，由此可见，计算特征点坐标精度远大于1mm，为毫米下一级精度。
[0189]
表1模型统计数据
[0190][0191]
[0192]
以上对本发明的实施例进行了详细说明，但所述内容仅为本发明的较佳实施例，不能被认为限定本发明的实施范围。凡依本发明申请范围所作的均等变化与改进，均应仍归属于本发明的专利涵盖范围之内。