台体型并联机构及其位置正解的求解方法与流程

本发明涉及一种台体型并联机构及其位置正解的求解方法，属于机器人
技术领域：
。
背景技术：
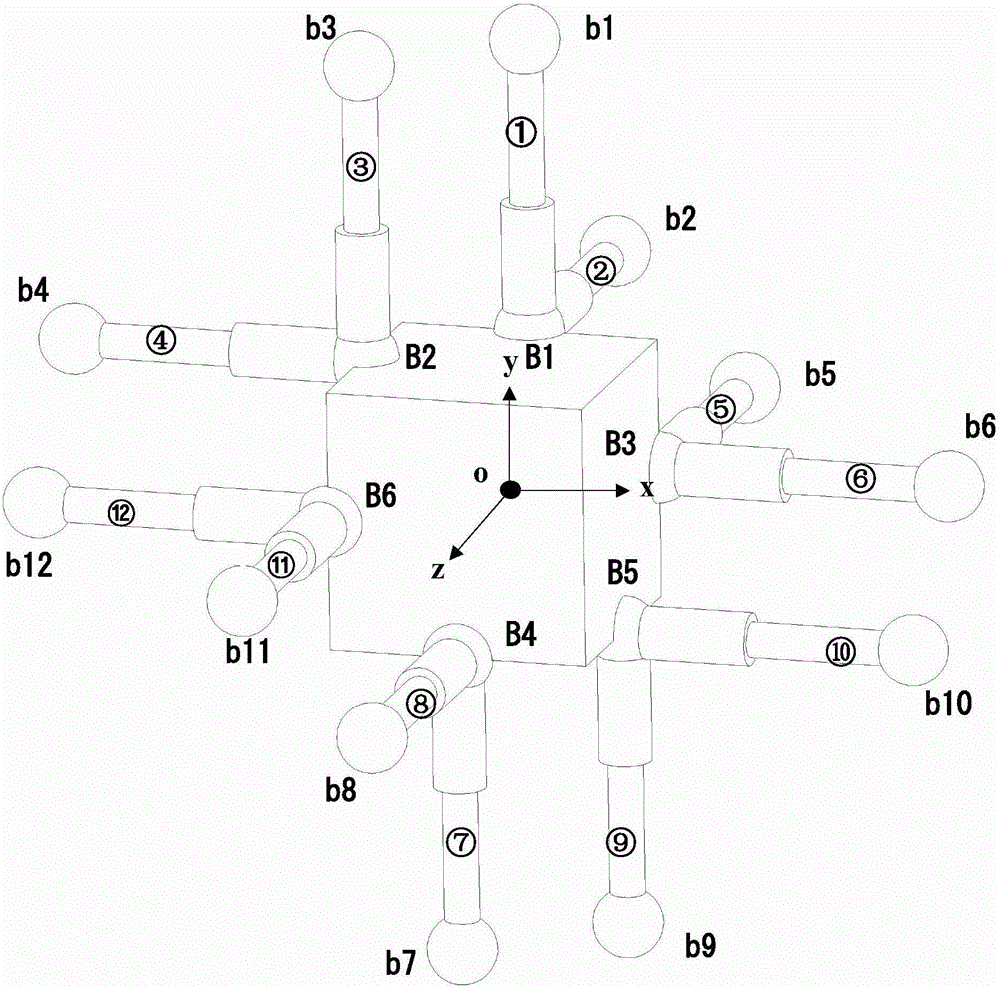
：并联机构最早出现在20世纪30年代。1931年，Gwinnett提出了一种基于球面并联机构的娱乐装置；1934年，Pollard设计了一种基于并联机构的汽车喷漆机器人；1947年，Gough发明了一种基于并联机构的六自由度轮胎检测装置；1965年，Stewart首次对Gough发明的并联机构进行了理论研究，提出六自由度并联机构，并设计出飞行模拟器的运动产生装置；1978年，Hunttichu首次提出将六自由度的Stewart并联机构作为机器人操作器。并联机构的研发已成为国际机构学界的研究热点，六杆并联机构是并联机构的一种特殊形式，具有六个自由度的调节方式，已广泛应用于国内外大科学工程项目。与串联机构相比，并联结构具有输出精度高、结构刚性好、承载能力强、便于控制等优点，其应用涉及到航空航天、机器人、交通运输、生物医疗等领域。根据几何构型不同，并联机构可分为平台型和台体型两种。相对于平台型并联机构，台体型并联机构的动、静平台上各球铰链的球心在空间呈任意分布而不局限于同一平面，因此，后者具有更广阔的应用前景。并联机构位置正解是指根据驱动输入量解算动平台的位置坐标和姿态矩阵，通常机构位置正解需要求解多元非线性方程组，在机构尺度综合、后续的运动控制、工作空间分析、奇异位形分析、零点位姿校对、运动标定、输出误差分析和轨迹控制等方面都需要获得机构的位置正解，机构位置正解已经成为机构学研究领域的热点之一。然而，由于台体型并联机构结构复杂，动平台运动位姿强耦合、非线性，使得其位置正解的计算极为困难。目前并联机构位置正解的算法主要分为两大类：数值法和解析法，数值法是通过数值迭代来求解约束方程组的，数学模型较为简单，易于建立，适用于任何并联机构，然而常用的牛顿迭代法在计算前需要给定一个合适的初值，同伦法计算可能有发散路径等，这些都会给计算带来负担，另外数值法计算效率低，且不能保证找到所有的解；解析法是通过消元消去约束方程中的若干个未知数，使得机构的输入输出方程成为只含一个未知数的高次方程，这样就能够得到动平台位姿的所有可能解，该方法不仅可以提供机构的几何特征和运动特性，而且单变量的输入输出方程对于运动学的其它方面(例如工作空间分析、奇异位形分析等)都有很大的理论参考价值。综上可知，寻求计算简洁、求解效率高的解析解算法具有实际意义。为此，国内外学者对台体型并联机构的位置正解问题进行了大量研究。据申请人了解，文献‘DirectKinematicsinAnalyticalFormofaGeneralGeometry5-4Fully-ParallelManipulator’解决了5-4台体型并联机构位置正解问题，消元处理后最终得到1元24次方程；文献‘DirectPositionalAnalysisforaKindof5-5PlatforminParallelRoboticMechanism’解决了5-5台体型并联机构位置正解问题，消元处理后最终得到1元40次方程；文献‘DirectPositionAnalysisoftheStewartPlatformMechanism’解决了6-3台体型并联机构位置正解问题，消元处理后最终得到1元16次方程；文献‘DirectKinematicsinAnalysisFormofthe6-4Fully-ParallelMechanism’解决了6-4台体型并联机构位置正解问题，消元处理后最终得到1元32次方程。然而，由于法国数学家伽罗华通过将方程的求解问题转化为确定对应的伽罗华群是否为可解群的问题，证明了一般五次以上方程的根式不可解性，上述台体型并联机构的位置正解问题最终都转化成五次以上的方程，其求解仍然需要借助数值法。因此，严格来讲，这类方法仅能被称为“半解析法”。综上所述，现有位置正解方法还不能实现台体型并联机构动平台位姿的全解析化，而且计算过程中往往会引入无用的复数根、增根，这就需要人为进行判断、筛选，无法实现数学机械化求解。究其根本原因，现有台体型并联机构的耦合度一般大于零，只有借助于多维搜索法才能够求出实数解。因此，亟需一种能够解决台体型并联机构位置正解无解析解或解析解推导困难、计算耗时等问题的“全解析法”。技术实现要素：本发明的目的在于：针对上述现有技术存在的缺点，提出一种结构简单、易加工、易装配的拓扑构型台体型并联机构，同时给出了其位置正解的求解方法，该方法物理意义清晰，计算量小，无增根和失根，计算方式简明，实现了位置正解的全解析解。为了达到以上目的，本发明提供了一种台体型并联机构，包括一个实心立方体形状的动平台，一个空心立方体形状的静平台和12条结构相同的支链，动平台和12条支链设置在静平台的容置腔内，初始状态下，静平台的几何中心与动平台的几何中心重合；12条支链中，每两条支链为一组呈一夹角布置于动平台上的6条棱边的中点，将6条棱边分为三组，每组包括不在同一平面且相互平行的两条棱边，支链由一移动副和两球面副串联而成。优选地，支链由一个下球铰链、一个内杆、一个外杆和一个共用球铰链依次串接组成，内杆套装在外杆内，并且内杆与外杆配合形成一移动副，使得内杆可沿轴向相对外杆移动，进而使支链可压短和拉长；下球铰链、共用球铰链为圆球体，内杆与下球铰链配合形成第一球面副，外杆与共用球铰链配合形成第二球面副。这样，通过驱动12条支链的移动副，可以实现动平台在静平台的容置腔内沿其空间任意方向平移和转动。优选地，下球铰链固定在静平台的内壁上。优选地，每组两条支链共用一个共用球铰链，12条支链中共有6个共用球铰链，6个共用球铰链分别固定于动平台的上后棱边、上左棱边、右后棱边、下前棱边、下右棱边、左前棱边的中点。优选地，每组两条支链之间的夹角为90°。综上可知，本发明的台体型并联机构包括一个动平台，一个静平台和12条支链，其中12条支链两两一组，每组两条支链垂直布置并且共用一个共用球铰链。该并联机构为一种六自由度12-6台体型全解耦并联机构，采用综合耦合度为零的拓扑构型，使得机构的位置正解有解析解。机构耦合度揭示了机构拓扑构型的复杂程度，耦合度越大(最小值为零)，机构内各单开链之间的耦合性越强，位置正解求解越困难。因此，只有当耦合度为零时，机构的位置正解才有解析解。通过计算机构内所有基本回路的约束度，并计算它们绝对值的和可以得到机构的耦合度。可见，并联机构的耦合度同时与动平台和静平台上铰链个数及铰链间的相对位置、每根支链内的铰链个数及类型、机构内的支链根数及支链配置方向都有关。设计耦合度为零的并联机构一直是学者们梦寐以求的目标，经计算，本发明的台体型并联机构的耦合度等于零。本发明还提供了一种台体型并联机构位置正解的求解方法，该方法包括以下步骤：第1步、将静平台固定在工作地面上，并在静平台的容置腔内设置动平台和12条支链，在静平台内建立坐标系oxyz，其中坐标系原点o与静平台的几何中心重合，x、y、z轴分别垂直指向静平台的右侧面、顶面、前面，初始状态下，动平台的几何中心与静平台的几何中心重合，动平台的6个外表面与静平台的6个内表面一一对应且平行设置，并且12条支链的长度相同；转至第2步；第2步、将动平台的中心点标记为P，其笛卡尔坐标为将固定于动平台上的6个共用球铰链的中心点依次标记为B1、B2、B3、B4、B5、B6，,其笛卡尔坐标分别为选取动平台上四个特征点的坐标为未知量，所述四个特征点为动平台的中心点和前3个共用球铰链的中心点，其笛卡尔坐标分别为假设将x0,y0,z0,x1,y1,z1,x2,y2,z2,x3,y3,z3设为待求的未知数，然后根据上述12个未知数列出后3个共用球铰链中心点的笛卡尔坐标的坐标解析式：转至第3步；第3步、驱动12条支链的移动副工作，以实现动平台在静平台的容置腔内沿任意方向运动，然后根据12条支链的下球铰链中心点与对应共用球铰链中心点之间的实时距离以及前3个共用球铰链中心点分别与动平台中心点之间的约束距离，建立(1)～(15)等15个二次相容方程式，将15个二次相容方程式分成三组，方程(1)～(5)构成第一组方程，其中方程(6)～(10)构成第二组方程，方程(11)～(15)构成第三组方程，|Bv1-bv1|2=x12+(y1-(n+L))2+(z1+n)2=l12---(1)]]>|Bv1-bv2|2=x12+(y1-n)2+(z1+(n+L))2=l22---(2)]]>|Bv4-bv7|2=(x1-2x0)2+(y1-2y0-(n+L))2+(z1-2z0+n)2=l72---(3)]]>|Bv4-bv8|2=(x1-2x0)2+(y1-2y0-n)2+(z1-2z0+(n+L))2=l82---(4)]]>|Bv1-Pv|2=(x1-x0)2+(y1-y0)2+(z1-z0)2=2n2---(5)]]>|Bv2-bv3|2=(x2+n)2+(y2-(n+L))2+z22=l32---(6)]]>|Bv2-bv4|2=(x2+(n+L))2+(y2-n)2+z22=l42---(7)]]>|Bv5-bv9|2=(x2-2x0+n)2+(y2-2y0-(n+L))2+(z2-2z0)2=l92---(8)]]>|Bv5-bv10|2=(x2-2x0+(n+L))2+(y2-2y0-n)2+(z2-2z0)2=l102---(9)]]>|Bv2-Pv|2=(x2-x0)2+(y2-y0)2+(z2-z0)2=2n2---(10)]]>|Bv3-bv5|2=(x3-n)2+y32+(z3+(n+L))2=l52---(11)]]>|Bv3-bv6|2=(x3-(n+L))2+y32+(z3+n)2=l62---(12)]]>|Bv6-bv11|2=(x3-2x0-n)2+(y3-2y0)2+(z3-2z0+(n+L))2=l112---(13)]]>|Bv6-bv12|2=(x3-2x0-(n+L))2+(y3-2y0)2+(z3-2z0+n)2=l122---(14)]]>|Bv3-Pv|2=(x3-x0)2+(y3-y0)2+(z3-z0)2=2n2---(15)]]>其中，设定支链的编号为j(j＝1,2，3，…12)，并将第j条支链的下球铰链中心点标记为bj，其笛卡尔坐标为将第j条支链的下球铰链中心点与对应共用球铰链中心点之间的实时距离设为lj，同时设定支链的初始长度为L，动平台的边长为2n；转至第4步；第4步、依次将第一组方程、第二组方程、第三组方程中的同构方程相减，得到(16)～(27)等12个线性相容方程：(1)-(2)⇒y1+z1=(-l12+l22)/(2L)---(16)]]>(3)-(4)⇒y0+z0=(-l12+l22+l72-l82)/(4L)---(17)]]>(1)-(3)⇒x0x1+y0y1+z0z1=(l12-l72)/4+x02+y02+z02+(n+L)y0-nz0---(18)]]>(5)-(1)⇒(n+L)y1-nz1=(n+L)y0-nz0-(l12+l72)/4+(x02+y02+z02)/2+3n2/2+(n+L)2/2---(19)]]>(6)-(7)⇒x2+y2=(-l32+l42)/(2L)---(20)]]>(8)-(9)⇒x0+y0=(-l32+l42+l92-l102)/(4L)---(21)]]>(6)-(8)⇒x0x2+y0y2+z0z2=(l32-l92)/4+x02+y02+z02-nx0+(n+L)y0---(22)]]>(10)-(6)⇒nx2-(n+L)y2=nx0-(n+L)y0+(l32+l92)/4-(x02+y02+z02)/2-3n2/2-(n+L)2/2---(23)]]>(11)-(12)⇒x3+z3=(l52-l62)/(2L)---(24)]]>(13)-(14)⇒x0+z0=(l52-l62-l112+l122)/(4L)---(25)]]>(11)-(13)⇒x0x3+y0y3+z0z3=(l52-l112)/4+x02+y02+z02+nx0-(n+L)z0---(26)]]>(15)-(11)⇒nx3-(n+L)z3=nx0-(n+L)z0-(l52+l112)/4+(x02+y02+z02)/2+3n2/2+(n+L)2/2---(27)]]>转至第5步；第5步、将上述12个线性相容方程分成四组，其中，方程(17)、(21)、(25)构成关于动平台位置的第Ⅰ组方程，并将第Ⅰ组方程表示成如下矩阵形式：011101110x0y0z0=14L-l12+l22+l72-l82l52-l62-l112+l122-l32+l42+l92-l102---(28),]]>方程(16)、(18)、(19)构成关于第一个共用球铰链中心点坐标的第Ⅱ组方程，并将第Ⅱ组方程表示成如下矩阵形式：011x0y0z00n+L-nx1y1z1=(-l12+l22)/(2L)(l12-l72)/4+x02+y02+z02+(n+L)y0-nz0(n+L)y0-nz0-(l12+l72)/4+(x02+y02+z02)/2+3n2/2+(n+L)2/2---(29),]]>方程(20)、(22)、(23)构成关于第二个共用球铰链中心点坐标的第Ⅲ组方程，并将第Ⅲ组方程表示成如下矩阵形式：110x0y0z0n-(n+L)0x2y2z2=(-l32+l42)/(2L)(l32-l92)/4+x02+y02+z02-nx0+(n+L)y0nx0-(n+L)y0+(l32+l92)/4-(x02+y02+z02)/2-3n2/2-(n+L)2/2---(30),]]>方程(24)、(26)、(27)构成关于第三个共用球铰链中心点坐标的第Ⅳ组方程，并将第Ⅳ组方程表示成如下矩阵形式：101x0y0z0n0-(n+L)x3y3z3=(l52-l62)/(2L)(l52-l112)/4+x02+y02+z02+nx0-(n+L)z0nx0-(n+L)z0-(l52+l112)/4+(x02+y02+z02)/2+3n2/2+(n+L)2/2---(31),]]>转至第6步；第6步、计算得到非齐次线性方程组(28)的系数矩阵的行列式如下：|011101110|=2≠0---(32)]]>当非齐次线性方程组(28)的系数矩阵非奇异时，该方程的解析解(即动平台位置坐标的解析解)如下：x0y0z0=14L011101110-1-l12+l22+l72-l82l52-l62-l112+l122-l32+l42+l92-l102---(33)]]>转至第7步；第7步、根据非齐次线性方程组(29)、(30)、(31)计算得到其系数矩阵的行列式，并根据上述行列式分别判断非齐次线性方程组(29)、(30)、(31)的系数矩阵的奇异性，当非齐次线性方程组(29)、(30)、(31)的系数矩阵非奇异时，能够直接获得6个共用球铰链中心点坐标的解析解，当非齐次线性方程组(29)、(30)、(31)的系数矩阵奇异时，需结合对应的共用球铰链中心点坐标的一个二次相容方程获得6个共用球铰链中心点坐标的解析解；转至第8步；第8步、采用x0,y0,z0,x1,y1,z1,x2,y2,z2,x3,y3,z312个未知数描述动平台的右侧面中心点坐标、顶面中心点坐标、前面中心点坐标，然后利用动平台的右侧面中心点坐标、顶面中心点坐标、前面中心点坐标以及动平台的中心点坐标描述动平台姿态的解析解，得到动平台位姿的全解析解。其中动平台位姿的全解析解是由动平台位置坐标的解析解和动平台姿态矩阵(R)的解析解共同构成。优选地，所述第7步中判断非齐次线性方程组(29)、(30)、(31)的系数矩阵的奇异性以及获得6个共用球铰链中心点坐标的解析解，包括如下步骤：S1、首先计算得到非齐次线性方程组(29)的系数矩阵的行列式如下：|011x0y0z00n+L-n|=(L+2n)x0---(34)]]>再根据x0是否为0，判断非齐次线性方程组(29)的系数矩阵的奇异性，若x0≠0，非齐次线性方程组(29)的系数矩阵非奇异，该方程的解析解如下：x1y1z1=011x0y0z00n+L-n-1(-l12+l22)/(2L)(l12-l72)/4+x02+y02+z02+(n+L)y0-nz0(n+L)y0-nz0-(l12+l72)/4+(x02+y02+z02)/2+3n2/2+(n+L)2/2---(35),]]>若x0＝0，非齐次线性方程组(29)的系数矩阵奇异，需要从非齐次线性方程组(29)中提取新的二元方程组(36)：11n+L-ny1z1=(-l12+l22)/(2L)(n+L)y0-nz0-(l12+l72)/4+(x02+y02+z02)/2+3n2/2+(n+L)2/2---(36)]]>根据二元方程组(36)计算其系数矩阵的行列式，如下：|11n+L-n|=-(L+2n)≠0---(37)]]>当二元方程组(36)的系数矩阵非奇异时，该方程组的解析解如下：y1z1=11n+L-n-1(-l12+l22)/(2L)(n+L)y0-nz0-(l12+l72)/4+(x02+y02+z02)/2+3n2/2+(n+L)2/2---(38)]]>然后根据方程(5)，获得x1的两个解析解：转至S2；S2、首先计算得到非齐次线性方程组(30)的系数矩阵的行列式如下：|110x0y0z0n-(n+L)0|=(L+2n)z0---(40)]]>再根据z0是否为0，判断非齐次线性方程组(30)的系数矩阵的奇异性，若z0≠0，非齐次线性方程组(30)的系数矩阵非奇异，该方程的解析解如下：x2y2z2=110x0y0z0n-(n+L)0-1(-l32+l42)/(2L)(l32-l92)/4+x02+y02+z02-nx0+(n+L)y0nx0-(n+L)y0+(l32+l92)/4-(x02+y02+z02)/2-3n2/2-(n+L)2/2---(41),]]>若z0＝0，非齐次线性方程组(30)的系数矩阵奇异，需要从非齐次线性方程组(30)中提取新的二元方程组(42)：11n-(n+L)x2y2=(-l32+l42)/(2L)nx0-(n+L)y0+(l32+l92)/4-(x02+y02+z02)/2-3n2/2-(n+L)2/2---(42)]]>根据二元方程组(42)计算其系数矩阵的行列式，如下：|11n-(n+L)|=-(L+2n)≠0---(43)]]>当二元方程组(42)的系数矩阵非奇异时，该方程组的解析解如下：x2y2=11n-(n+L)-1(-l32+l42)/(2L)nx0-(n+L)y0+(l32+l92)/4-(x02+y02+z02)/2-3n2/2-(n+L)2/2---(44)]]>然后根据方程(10)，获得z2的两个解析解：转至S3；S3、首先计算得到非齐次线性方程组(31)的系数矩阵的行列式如下：|101x0y0z0n0-(n+L)|=-(L+2n)y0---(46)]]>再根据y0是否为0，判断非齐次线性方程组(31)的系数矩阵的奇异性，若y0≠0，非齐次线性方程组(31)的系数矩阵非奇异，该方程的解析解如下：x3y3z3=101x0y0z0n0-(n+L)-1(l52+l62)/(2L)(l52-l112)/4+x02+y02+z02+nx0-(n+L)z0nx0-(n+L)z0-(l52+l112)/4+(x02+y02+z02)/2+3n2/2+(n+L)2/2---(47),]]>若y0＝0，非齐次线性方程组(31)的系数矩阵奇异，需要从非齐次线性方程组(31)中提取新的二元方程组(48)：11n-(n+L)x3z3=(l52-l62)/(2L)nx0-(n+L)z0-(l52+l112)/4+(x02+y02+z02)/2+3n2/2+(n+L)2/2---(48)]]>根据二元方程组(48)计算其系数矩阵的行列式，如下：|11n-(n+L)|=-(L+2n)≠0---(49)]]>当二元方程组(48)的系数矩阵非奇异时，该方程组的解析解如下：x3z3=11n-(n+L)-1(l52-l62)/(2L)nx0-(n+L)z0-(l52+l112)/4+(x02+y02+z02)/2+3n2/2+(n+L)2/2---(50)]]>然后根据方程(15)，获得y3的两个解析解：y3=±2n2-(x3-x0)2-(z3-z0)2---(51)]]>至此获得前3个共用球铰链的中心点坐标进一步优选地，所述第8步中动平台姿态解析解的获取方法具体如下：(a)对前3个共用球铰链的中心点坐标(x1,y1,z1)、(x2,y2,z2)、(x3,y3,z3)是否为唯一解进行判断，若(x1,y1,z1)、(x2,y2,z2)、(x3,y3,z3)是唯一解，则选定前3个共用球铰链的中心点坐标若(x1,y1,z1)、(x2,y2,z2)、(x3,y3,z3)不是唯一解，则根据(52)式筛选出符合要求的前3个共用球铰链的中心点坐标x0+x1-x2-x3=0y0+y1-y2-y3=0z0+z1-z2-z3=0---(52);]]>(b)根据前3个共用球铰链的中心点坐标获得后3个共用球铰链的中心点坐标(c)将动平台的右侧面中心点坐标设为根据该点与第三个共用球铰链中心点、第5个共用球铰链中心点、动平台中心点的几何关系，获得该点坐标的解析解：Pvright=13(Pv+Pv3+Bv5)-13n(Bv5-Bv3)×(Pv-Bv3)---(53)]]>其中，“×”表示矢量的叉乘运算；(d)将动平台的顶面中心点坐标设为根据该点与第一个共用球铰链中心点、第二个共用球铰链中心点、动平台中心点的几何关系，获得该点坐标的解析解：Pvtop=13(Pv+Bv1+Bv2)-13n(Pv-Bv1)×(Bv2-Bv1)---(54);]]>(e)将动平台的前面中心点坐标设为根据该点与第四个共用球铰链中心点、第六个共用球铰链中心点、动平台中心点的几何关系，获得该点坐标的解析解：Pvfront=13(Pv+Bv4+Bv6)-13n(Bv4-Pv)×(Bv6-Pv)---(55);]]>(f)设定动平台的姿态矩阵为(R)，根据动平台的右侧面中心点坐标顶面中心点坐标前面中心点坐标以及动平台的中心点坐标描述动平台姿态矩阵(R)的解析解如下：(R)=1n(Pvright-Pv,Pvtop-Pv,Pvfront-Pv)---(56)]]>其中，动平台位置坐标的解析解和动平台姿态矩阵(R)的解析解共同构成了动平台位姿的全解析解。本发明的优点是内杆与外杆相配合组成伸缩式驱动杆，通过驱动杆的伸缩可以实现动平台确定的连续运动，机械结构简单，易加工，易装配，并且该机构具有12条支链和明确的工作空间，耦合度为零，使得该机构具有简明的、全解析形式的位置正解，运动学运算效率高，无增根和失根，能够实现数学机械化求解，为机器人的实际应用提供了理论保障。附图说明下面结合附图对本发明作进一步的说明。图1为本发明一个实施例的结构示意图。图2为本发明中动平台与12根支链的配置关系图，其中oxyz代表固结在静平台上的坐标系，位于支链中间的数字①～代表对应支链的编号，位于支链一端的符号B1～B6代表对应支链的共用球铰链中心，位于支链另一端的符号b1～b12代表对应支链的下球铰链中心；图3为本发明台体型并联机构位置正解的求解方法流程图。图中：1.动平台，2.静平台，3.下球铰链，4.内杆，5.外杆，6.共用球铰链。具体实施方式下面结合具体的实施例对本发明作进一步说明。实施例一本实施例的12-6台体型全解耦并联机构，其结构如图1所示，包括一个动平台1，一个静平台2和12条支链，动平台1为实心立方体，静平台2为空心立方体，动平台1和12条支链设置在静平台2的容置腔内，初始状态下，静平台2的几何中心与动平台1的几何中心重合。12条支链的结构相同，均由一个下球铰链3、一个内杆4、一个外杆5和一个共用球铰链6依次串接组成，下球铰链3、共用球铰链6均为圆球体，内杆4为实心圆柱体，外杆5为空心圆柱体，且外杆5的内径与内杆4的外径相同，将内杆4套装在外杆5内，二者过盈配合形成一移动副，使得内杆4在外杆5内部沿着其轴向移动，进而使支链可压短和拉长，内杆4与下球铰链3配合形成第一球面副，外杆5与共用球铰链6配合形成第二球面副。12条支链中，每两条支链为一组，每组两条支链垂直布置且共用一个共用球铰链6，12条支链中共有6个共用球铰链，6个共用球铰链6分别固定于动平台1的上后棱边、上左棱边、右后棱边、下前棱边、下右棱边、左前棱边的中点，12个下球铰链3固定在静平台2的内壁上。结合图2和图3，台体型并联机构位置正解的求解方法，具体步骤如下：准备工作：将静平台2固定在工作地面上，并在静平台2的容置腔内设置动平台1和12条支链，然后在静平台2内建立坐标系oxyz，其中坐标系原点o与静平台2的几何中心重合，x、y、z轴分别垂直指向静平台2的右侧面、顶面、前面；初始状态下，动平台1的几何中心与静平台2的几何中心重合，动平台1的6个外表面与静平台2的6个内表面一一对应且平行设置，并且12条支链的初始长度(即初始状态下，每条支链的下球铰链3中心点与对应共用球铰链6中心点之间的距离)相同。第1步、将动平台1的中心点标记为P，其笛卡尔坐标为将固定于动平台1上的6个共用球铰链6的中心点依次标记为B1、B2、B3、B4、B5、B6，,其笛卡尔坐标分别为选取动平台1中心点和前3个共用球铰链6中心点等四个特征点的坐标为未知量，四个特征点的笛卡尔坐标分别为假设再将x0,y0,z0,x1,y1,z1,x2,y2,z2,x3,y3,z3等12个标量设为待求的未知数，然后根据上述12个未知数列出后3个共用球铰链6中心点的笛卡尔坐标的坐标解析式：第2步、驱动12条支链的移动副工作，以实现动平台1在静平台2的容置腔内沿任意方向运动，然后根据12条支链的下球铰链3中心点与对应共用球铰链6中心点之间的实时距离(即支链的实时长度，具体为b1与B1、b2与B1、b3与B2、b4与B2、b5与B3、b6与B3、b7与B4、b8与B4、b9与B5、b10与B5、b11与B6、b12与B6之间的实时距离)以及前3个共用球铰链6中心点分别与动平台1中心点之间的约束距离(具体为B1与P之间的距离，B2与P之间的距离，B3与P之间的距离)，建立(1)～(15)等15个二次相容方程式，将15个二次相容方程式分成三组，其中，方程(1)～(5)构成第一组方程，方程(6)～(10)构成第二组方程，方程(11)～(15)构成第三组方程，|B1v-b1v|2=x12+(y1-(n+L))2+(z1+n)2=l12---(1)]]>|Bv1-bv2|2=x12+(y1-n)2+(z1+(n+L))2=l22---(2)]]>|Bv4-bv7|2=(x1-2x0)2+(y1-2y0-(n+L))2+(z1-2z0+n)2=l72---(3)]]>|Bv4-bv8|2=(x1-2x0)2+(y1-2y0-n)2+(z1-2z0+(n+L))2=l82---(4)]]>|Bv1-Pv|2=(x1-x0)2+(y1-y0)2+(z1-z0)2=2n2---(5)]]>|Bv2-bv3|2=(x2+n)2+(y2-(n+L))2+z22=l32---(6)]]>|Bv2-bv4|2=(x2+(n+L))2+(y2-n)2+z22=l42---(7)]]>|Bv5-bv9|2=(x2-2x0+n)2+(y2-2y0-(n+L))2+(z2-2z0)2=l92---(8)]]>|Bv5-bv10|2=(x2-2x0+(n+L))2+(y2-2y0-n)2+(z2-2z0)2=l102---(9)]]>|Bv2-Pv|2=(x2-x0)2+(y2-y0)2+(z2-z0)2=2n2---(10)]]>|Bv3-bv5|2=(x3-n)2+y32+(z3+(n+L))2=l52---(11)]]>|Bv3-bv6|2=(x3-(n+L))2+y32+(z3+n)2=l62---(12)]]>|Bv6-bv11|2=(x3-2x0-n)2+(y3-2y0)2+(z3-2z0+(n+L))2=l112]]>(13)]]>|Bv6-bv12|2=(x3-2x0-(n+L))2+(y3-2y0)2+(z3-2z0+n)2=l122---(14)]]>|Bv3-Pv|2=(x3-x0)2+(y3-y0)2+(z3-z0)2=2n2---(15)]]>其中，设定支链的编号为j(j＝1,2，3，…12)，并将第j条支链的下球铰链3中心点标记为bj(12个下球铰链3的中心点依次被标记为b1、b2、b3、b4、b5、b6、b7、b8、b9、b10、b11、b12)，其笛卡尔坐标为将第j条支链的下球铰链3中心点与对应共用球铰链6中心点之间的实时距离设为lj(即支链的实时长度，12条支链的实时长度依次为l1、l2、l3、l4、l5、l6、l7、l8、l9、l10、l11、l12)，同时设定每条支链的初始长度为L，动平台1的边长为2n。第3步、根据同构关系依次将第一组方程、第二组方程、第三组方程中的同构方程相减，得到(16)～(27)等12个线性相容方程：(1)-(2)⇒y1+z1=(-l12+l22)/(2L)---(16)]]>(3)-(4)⇒y0+z0=(-l12+l22+l72-l82)/(4L)---(17)]]>(1)-(3)⇒x0x1+y0y1+z0z1=(l12-l72)/4+x02+y02+z02+(n+L)y0-nz0---(18)]]>(5)-(1)⇒(n+L)y1-nz1=(n+L)y0-nz0-(l12+l72)/4+(x02+y02+z02)/2+3n2/2+(n+L)2/2---(19)]]>(6)-(7)⇒x2+y2=(-l32+l42)/(2L)---(20)]]>(8)-(9)⇒x0+y0=(-l32+l42+l92-l102)/(4L)---(21)]]>(6)-(8)⇒x0x2+y0y2+z0z2=(l32-l92)/4+x02+y02+z02-nx0+(n+L)y0---(22)]]>(10)-(6)⇒nx2-(n+L)y2=nx0-(n+L)y0+(l32+l92)/4-(x02+y02+z02)/2-3n2/2-(n+L)2/2---(23)]]>(11)-(12)⇒x3+z3=(l52-l62)/(2L)---(24)]]>(13)-(14)⇒x0+z0=(l52-l62-l112+l122)/(4L)---(25)]]>(11)-(13)⇒x0x3+y0y3+z0z3=(l52-l112)/4+x02+y02+z02+nx0-(n+L)z0---(26)]]>(15)-(11)⇒nx3-(n+L)z3=nx0-(n+L)z0-(l52+l112)/4+(x02+y02+z02)/2+3n2/2+(n+L)2/2---(27)]]>将上述12个线性相容方程分成四组，其中方程(17)、(21)、(25)构成关于动平台1位置的第Ⅰ组方程，并将第Ⅰ组方程表示成如下矩阵形式：011101110x0y0z0=14L-l12+l22+l72-l82l52-l62-l112+l122-l32+l42+l92-l102---(28),]]>方程(16)、(18)、(19)构成关于第一个共用球铰链6中心点坐标的第Ⅱ组方程，并将第Ⅱ组方程表示成如下矩阵形式：011x0y0z00n+L-nx1y1z1=(-l12+l22)/(2L)(l12-l72)/4+x02+y02+z02+(n+L)y0-nz0(n+L)y0-nz0-(l12+l72)/4+(x02+y02+z02)/2+3n2/2+(n+L)2/2---(29),]]>方程(20)、(22)、(23)构成关于第二个共用球铰链6中心点坐标的第Ⅲ组方程，并将第Ⅲ组方程表示成如下矩阵形式：110x0y0z0n-(n+L)0x2y2z2=(-l32+l42)/(2L)(l32-l92)/4+x02+y02+z02-nx0+(n+L)y0nx0-(n+L)y0+(l32+l92)/4-(x02+y02+z02)/2-3n2/2-(n+L)2/2---(30),]]>方程(24)、(26)、(27)构成关于第三个共用球铰链6中心点坐标的第Ⅳ组方程，并将第Ⅳ组方程表示成如下矩阵形式：101x0y0z0n0-(n+L)x3y3z3=(l52-l62)/(2L)(l52-l112)/4+x02+y02+z02+nx0-(n+L)z0nx0-(n+L)z0-(l52+l112)/4+(x02+y02+z02)/2+3n2/2+(n+L)2/2---(31).]]>第4步、计算得到非齐次线性方程组(28)的系数矩阵的行列式如下：|011101110|=2≠0---(32)]]>当非齐次线性方程组(28)的系数矩阵非奇异时，该方程的唯一解析解(即动平台位置的解析解)如下：x0y0z0=14L011101110-1-l12+l22+l72-l82l52-l62-l112+l122-l32+l42+l92-l102---(33).]]>第5步、计算得到非齐次线性方程组(29)的系数矩阵的行列式，|011x0y0z00n+L-n|=(L+2n)x0---(34)]]>再根据x0是否为0，判断非齐次线性方程组(29)的系数矩阵的奇异性，若x0≠0，非齐次线性方程组(29)的系数矩阵非奇异，该方程的解析解(即第一个共用球铰链6位置的解析解)如下，x1y1z1=011x0y0z00n+L-n-1(-l12+l22)/(2L)(l12-l72)/4+x02+y02+z02+(n+L)y0-nz0(n+L)y0-nz0-(l12+l72)/4+(x02+y02+z02)/2+3n2/2+(n+L)2/2---(35),]]>若x0＝0，非齐次线性方程组(29)的系数矩阵奇异，需要从非齐次线性方程组(29)中提取新的二元方程组(36)，11n+L-ny1z1=(-l12+l22)/(2L)(n+L)y0-nz0-(l12+l72)/4+(x02+y02+z02)/2+3n2/2+(n+L)2/2---(36)]]>根据二元方程组(36)计算其系数矩阵的行列式，|11n+L-n|=-(L+2n)≠0---(37)]]>当二元方程组(36)的系数矩阵非奇异时，该方程组的解析解如下，y1z1=11n+L-n-1(-l12+l22)/(2L)(n+L)y0-nz0-(l12+l72)/4+(x02+y02+z02)/2+3n2/2+(n+L)2/2---(38)]]>然后根据方程(5)，获得x1的两个解析解，x1=±2n2-(y1-y0)2-(z1-z0)2---(39);]]>计算得到非齐次线性方程组(30)的系数矩阵的行列式，|110x0y0z0n-(n+L)0|=(L+2n)z0---(40)]]>再根据z0是否为0，判断非齐次线性方程组(30)的系数矩阵的奇异性，若z0≠0，非齐次线性方程组(30)的系数矩阵非奇异，该方程的解析解(即第二个共用球铰链6位置的解析解)如下：x2y2z2=110x0y0z0n-(n+L)0-1(-l32+l42)/(2L)(l32-l92)/4+x02+y02+z02-nx0+(n+L)y0nx0-(n+L)y0+(l32+l92)/4-(x02+y02+z02)/2-3n2/2-(n+L)2/2---(41),]]>若z0＝0，非齐次线性方程组(30)的系数矩阵奇异，需要从非齐次线性方程组(30)中提取新的二元方程组(42)，11n-(n+L)x2y2=(-l32+l42)/(2L)nx0-(n+L)y0+(l32+l92)/4-(x02+y02+z02)/2-3n2/2-(n+L)2/2---(42)]]>根据二元方程组(42)计算其系数矩阵的行列式，|11n-(n+L)|=-(L+2n)≠0---(43)]]>当二元方程组(42)的系数矩阵非奇异时，该方程组的解析解，x2y2=11n-(n+L)-1(-l32+l42)/(2L)nx0-(n+L)y0+(l32+l92)/4-(x02+y02+z02)/2-3n2/2-(n+L)2/2---(44)]]>然后根据方程(10)，获得z2的两个解析解，z2=±2n2-(x2-x0)2-(y2-y0)2---(45);]]>计算得到非齐次线性方程组(31)的系数矩阵的行列式，|101x0y0z0n0-(n+L)|=-(L+2n)y0---(46)]]>再根据y0是否为0，判断非齐次线性方程组(31)的系数矩阵的奇异性，若y0≠0，非齐次线性方程组(31)的系数矩阵非奇异，该方程的解析解(即第三个共用球铰链6位置的解析解)如下，x3y3z3=101x0y0z0n0-(n+L)-1(l52+l62)/(2L)(l52-l112)/4+x02+y02+z02+nx0-(n+L)z0nx0-(n+L)z0-(l52+l112)/4+(x02+y02+z02)/2+3n2/2+(n+L)2/2---(47),]]>若y0＝0，非齐次线性方程组(31)的系数矩阵奇异，需要从非齐次线性方程组(31)中提取新的二元方程组(48)，11n-(n+L)x3z3=(l52-l62)/(2L)nx0-(n+L)z0-(l52+l112)/4+(x02+y02+z02)/2+3n2/2+(n+L)2/2---(48)]]>根据二元方程组(48)计算其系数矩阵的行列式，|11n-(n+L)|=-(L+2n)≠0---(49)]]>当二元方程组(48)的系数矩阵非奇异时，该方程组的解析解如下，x3z3=11n-(n+L)-1(l52-l62)/(2L)nx0-(n+L)z0-(l52+l112)/4+(x02+y02+z02)/2+3n2/2+(n+L)2/2---(50)]]>然后根据方程(15)，获得y3的两个解析解，y3=±2n2-(x3-x0)2-(z3-z0)2---(51)]]>至此获得前3个共用球铰链6的中心点坐标第6步、采用x0,y0,z0,x1,y1,z1,x2,y2,z2,x3,y3,z312个未知数描述动平台1的右侧面中心点坐标、顶面中心点坐标、前面中心点坐标，然后利用动平台1的右侧面中心点坐标、顶面中心点坐标、前面中心点坐标以及动平台1的中心点坐标描述动平台1姿态的解析解，得到动平台1位姿的全解析解；具体方法如下：(a)对前3个共用球铰链6的中心点坐标(x1,y1,z1)、(x2,y2,z2)、(x3,y3,z3)是否为唯一解进行判断，若(x1,y1,z1)、(x2,y2,z2)、(x3,y3,z3)是唯一解，则选定前3个共用球铰链6的中心点坐标若(x1,y1,z1)、(x2,y2,z2)、(x3,y3,z3)不是唯一解，则根据(52)式筛选出符合要求的前3个共用球铰链6的中心点坐标x0+x1-x2-x3=0y0+y1-y2-y3=0z0+z1-z2-z3=0---(52);]]>(b)根据前3个共用球铰链6的中心点坐标获得后3个共用球铰链6的中心点坐标(c)将动平台1的右侧面中心点坐标设为根据该点与第三个共用球铰链6中心点、第5个共用球铰链6中心点、动平台1中心点的几何关系，获得该点坐标的解析解：Pvright=13(Pv+Pv3+Bv5)-13n(Bv5-Bv3)×(Pv-Bv3)---(53)]]>其中，“×”表示矢量的叉乘运算；(d)将动平台1的顶面中心点坐标设为根据该点与第一个共用球铰链6中心点、第二个共用球铰链6中心点、动平台1中心点的几何关系，获得该点坐标的解析解：Pvtop=13(Pv+Bv1+Bv2)-13n(Pv-Bv1)×(Bv2-Bv1)---(54);]]>(e)将动平台1的前面中心点坐标设为根据该点与第四个共用球铰链6中心点、第六个共用球铰链6中心点、动平台1中心点的几何关系，获得该点坐标的解析解：Pvfront=13(Pv+Bv4+Bv6)-13n(Bv4-Pv)×(Bv6-Pv)---(55);]]>(f)设定动平台1的姿态矩阵为(R)，根据动平台1的右侧面中心点坐标顶面中心点坐标前面中心点坐标以及动平台1的中心点坐标描述动平台1姿态矩阵(R)的解析解如下：(R)=1n(Pvright-Pv,Pvtop-Pv,Pvfront-Pv)---(56)]]>其中，动平台1位置坐标的解析解和动平台1姿态矩阵(R)的解析解共同构成了动平台1位姿的全解析解。至此，完成台体型并联机构位置正解的计算，得到动平台1位姿的全解析解，将上述方法命名为“解析六步法”，该方法求解难度低，步骤简练，有效地降低了计算耗时。除上述实施例外，本发明还可以有其他实施方式。凡采用等同替换或等效变换形成的技术方案，均落在本发明要求的保护范围。当前第1页1 2 3