基于焊接机器人系统层次划分的可靠性模糊预计方法与流程

本发明涉及机器人安全控制技术领域，特别是一种基于焊接机器人系统层次划分的可靠性模糊预计方法。

背景技术：

机器人产业作为众多领域中的关键产业，不仅仅吸引着国内厂商的不断加码，更有来自国外企业的抢食。一方面，能够帮助人类承担许多危险工作的稳定性好、可靠性高的工业机器人，受到了越来越多的企业的青睐。另一方面，企业面临着更加苛刻的客户要求，使得产品的研发面临着“更加可靠”、“更加快捷”、“更加便宜”的挑战。为了应对这一严酷的挑战企业不得不寻找一个有效的可靠性新思路。随着对产品要求的越来越严格，企业开始认识到在产品寿命周期中，可靠性设计的重要性。可靠性工程实施的越晚，后期所要支付的费用就会越高，这使得企业不得不主动地开展可靠性工作。

机器人可靠性暴露出的问题逐渐受到企业领导以及相关领域专家的重视。为解决这一问题许多专家学者开始把相应理论知识运用到机器人行业的整个设计过程中，主要涉及到机器人的故障树分析、故障模式影响分析、可靠性预计、分配等方面。针对焊接机器人可靠性预计方面：chenluyi等人提出了基于遗传算法的工业机器人可靠性预计方法。陈胜军给出了工业机器人的可靠性预计模型和算法并将理论与实际结合确定了机器人的mtbf值。杨强等建立了机构运动的可靠性模型,并为机构运动的可靠性指标给出了相关评价方法。许冯平等提出了将模糊数学与可靠性理论相结合的一种模糊评判方法，并将该方法运用到了管道机器人的可靠性评价上。tiewang等人提出了一种应用于受力为正态分布，强度为威布尔分布的标准模糊可靠性算法。仉立军,兰小玲等为描述机器人的状态变化建立了markov模型的移动机器人可靠性计算方法。孙志佳结合工业机器人可靠性与维修性分析结果，运用递阶层次法和信息熵原理，有效的实现了机器人的可靠性与维修性的综合评价。冯虎田等定义了机器人动作的可靠性指标，并给出了其指标的计算方法。

目前电子元器件的失效率相对来说比较成熟，但是对于机械零部件来说并不成熟，而且对于含有许多自制件的系统来说其可靠性水平更是难以预计。对于焊接机器人系统而言，其既含有大量的电子元器件又含有机械零部件，一般的可靠性预计方法都不能更精确的预计焊接机器人系统的可靠性水平，采用传统的专家评分法虽然可以为没有可靠性数据的自制件和零部件系统进行可靠性预计，但是其可靠性预计结果受人为主观因素的影响较大。

技术实现要素：

本发明目的在于提供一种基于焊接机器人系统层次划分的可靠性模糊预计方法，既能减少元器件计数法对可靠性数据收集的时间，又能克服传统专家评分法的人为主观因素的影响。

实现本发明目的的技术解决方案为：一种基于焊接机器人系统层次划分的可靠性模糊预计方法，包含以下步骤：

步骤1，根据焊接机器人系统组成及其功能进行层次划分；

步骤2，建立焊接机器人系统以及控制子系统的可靠性框图；

步骤3，构建焊接机器人系统以及控制子系统的可靠性数学模型；

步骤4，确定焊接机器人控制子系统的失效率；

步骤5，确定焊接机器人系统可靠性预计的影响因素；

步骤6，确定各子系统的评分系数；

步骤7，确定焊接机器人系统的mtbf值。

作为一种具体示例，步骤1所述根据焊接机器人系统组成及其功能进行层次划分，具体为：

将焊接机器人系统抽象成控制子系统、焊接子系统、本体子系统三个子系统，根据子系统的划分编制相应的焊接机器人系统代码表，如下表1所示：

表1

作为一种具体示例，步骤3所述构建焊接机器人系统以及控制子系统的可靠性数学模型，步骤如下：

(3.1)整个机器人系统由三个简化的子系统彼此串联而成，且可靠性数学模型为：

r(t)＝rr(t)×rc(t)×rw(t)(1)

式(1)中，r(t)为系统的可靠度；rr(t)、rc(t)、rw(t)分别为焊接机器人的本体子系统、控制子系统、焊接子系统的可靠度；

(3.2)对于单个串联的子系统而言，可靠度根据组成子系统的零部件的故障率求出，如果各零部件之间的连接是通过串联建立的，那么子系统的故障率使用各零部件故障率相乘得出，机器人的子系统可靠度计算公式如下：

rs(t)＝r1(t)×r2(t)×r3(t)×......×rn(t)(2)

式(2)中，rs(t)为机器人子系统的可靠度；ri(t)为第i个串联的零件可靠度，i＝1,2,…,n。

作为一种具体示例，步骤4所述确定焊接机器人控制子系统的失效率，具体如下：

根据控制子系统的元器件组成，参考gjb/z299《电子设备可靠性预计手册》中所提供的数学模型，假设焊接机器人系统中所有零部件的密度函数类型都呈指数分布，根据控制子系统的可靠性数学模型，经过统计分析和数学计算，得到焊接机器人控制子系统的失效率，也即控制子系统的mtbf值。

作为一种具体示例，步骤5所述确定焊接机器人系统可靠性预计的影响因素，具体包括复杂程度、工作时间、技术水平、环境条件。

作为一种具体示例，步骤6所述确定各子系统的评分系数，具体如下：

(6.1)建立机器人系统的评分因素模糊语言集

表2给定了pr1400焊接机器人系统可靠性评价因素的等级评价标准：

表2评价因素等级评价标准

各评价因素等级以及相对重要性模糊数如下表3示：

表3各评价因素等级及相对重要性模糊数

(6.2)确定专家权重

根据专家自身的权重值bik和各项评价因素的权重值wij，专家k在第i项评价因素上的得分为：

式中：i表示项目因素序列，i＝1,2,3,4；

j表示各项因素的级别序列，j＝1,2,3,4,5；

k表示专家的序列，k＝1,2,3,4,5；

将专家k的观点重要度进行归一化处理，即得专家k的权重rk表达式为：

wi表示第i个项目的评分；

(6.3)专家评分

(6.4)建立焊接机器人系统评分系数ωi求解模型

①求焊接机器人系统评分系数ωi的过程，就是求n个模糊数的模糊权重算术平均值的过程，模糊权重算术平均值的计算公式如下：

式中：代表n个待定权重的模糊数；代表n个模糊数的模糊权重；

②利用质心法对模糊集合进行去模糊化处理，其中定义为去模糊化后模糊集所对应的准确值，则：

其中定义为去模糊化后模糊集所对应的准确值；代表n个待定权重的模糊数；代表n个模糊数的模糊权重；a,d代表上下边界；u代表去模糊权重系数，μ1+μ2+μ3+μ4＝1；

当模糊集由其λ截集表示时，则：

代表模糊集，λ截集代表系统内某个元器件的工作故障率；l和h代表评定因素语言模糊变量的上下界；u代表并集运算处理；

计算下式(10)、(11)，并将计算结果带入等式(6)即可求出模糊集合去模糊化后的清晰值：

当△λi＝1/n，并且λi＝i/n,i＝0,1,2,…,n时，等式(8)、(9)简化为：

本发明与现有技术相比，其显著优点为：(1)不需要对焊接机器人系统的所有零部件进行可靠性预计，就可以最终确定pr1400焊接机器人系统的mtbf值；(2)弥补了自制件和某些机械零部件可靠性数据缺乏的不足，同时既减少了元器件计数法对可靠性数据收集的时间又克服了传统专家评分法的弊端。

附图说明

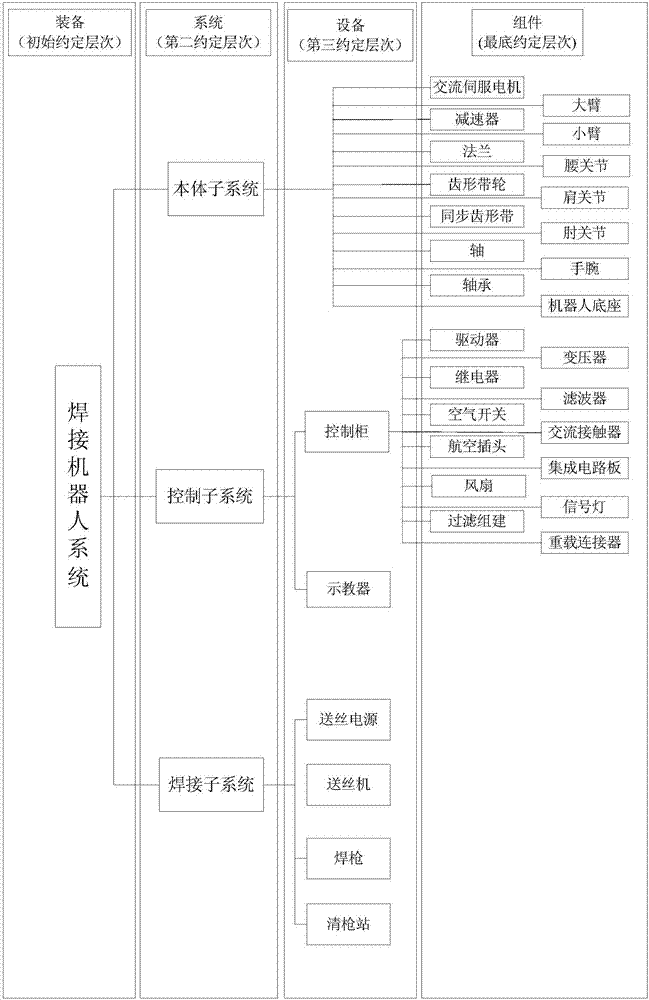
图1为本发明中焊接机器人系统的组成结构图。

图2为焊接机器人系统层次划分图。

图3为焊接机器人系统整体可靠性框图。

图4为焊接机器人系统控制子系统的可靠性框图。

具体实施方式

本发明提出的基于焊接机器人系统层次划分的可靠性模糊预计方法，包括以下步骤：

步骤1，根据焊接机器人系统组成及其功能进行层次划分。

1.2详细了解焊接机器人系统的结构及零部件组成。

1.3根据焊接机器人的组成结构以及所实现的功能进行层次划分，将焊接机器人系统抽象成控制子系统，焊接子系统、本体子系统三个子系统。各子系统的组成部分如下：

(一)机器人的本体子系统

通常包括基座、肩关节、下臂、上臂、手腕等关键结构。

(二)机器人的控制子系统

包括硬件系统、和软件系统。例如：伺服驱动器、变压器、集成电路板、可编程逻辑控制器、供电回路单元、滤波器、传感器、示教器等。

(三)机器人的焊接子系统

包括焊接电源、送丝机、焊枪、清枪站等组成同时根据子系统的划分编制相应的焊接机器人系统代码表如下表1所示。

表1pr1400焊接机器人系统名称及代码

步骤2，建立焊接机器人系统以及控制子系统的可靠性框图。

步骤3，构建焊接机器人系统以及控制子系统的可靠性数学模型。

(3.1)通过步骤2的分析可知，整个机器人系统可以由三个简化的子系统彼此串联而成，它的可靠性模型为：

r(t)＝rr(t)×rc(t)×rw(t)(1)

式(1)中：r(t)为系统的可靠度；rr(t)、rc(t)、rw(t)分别为焊接机器人的本体子系统、控制子系统、焊接子系统的可靠度；

(3.2)同理，对于单个串联的子系统而言，其可靠度可根据组成子系统的零部件的故障率求出，如果各零部件之间的连接是通过串联建立的，那么子系统的故障率可以使用各零部件故障率相乘得出。机器人的子系统可靠度计算公式如下：

rs(t)＝r1(t)×r2(t)×r3(t)×......×rn(t)(2)

式(2)中：rs(t)为机器人子系统的可靠度；ri(t)为第i个串联的零件可靠度，i＝1,2,…,n。

因此，根据上述方法建立了整机-子系统层面的焊接机器人可靠性框图及其数学模型。同时可以根据整机-子系统框图和模型建立子系统-零部件层面的可靠性框图及其数学模型。

步骤4，确定焊接机器人控制子系统的失效率。

根据控制子系统的元器件组成，参考gjb/z299《电子设备可靠性预计手册》中所提供的数学模型，假设焊接机器人系统中所有零部件的密度函数类型都呈指数分布，根据控制子系统的可靠性数学模型，经过大量统计分析和数学计算，得到焊接机器人控制子系统的失效率，也即控制子系统的mtbf值。

步骤5，确定焊接机器人系统可靠性预计的影响因素。

影响焊接机器人可靠性的因素很多，在实际工程中通常考虑的可靠性因素有复杂程度、工作时间、技术水平、环境条件等。

步骤6，确定各子系统的评分系数。

(6.1)建立机器人系统的评分因素模糊语言集。

用确定值来表达评价因素误差较大，需要采用有一定变化范围的模糊区间来评定。

表2给定了焊接机器人系统可靠性评价因素的等级评价标准。

表2评价因素等级评价标准

各评价因素等级以及相对重要性模糊数如下表3示：

表3各评价因素等级及相对重要性模糊数

(6.2)确定专家权重

邀请在焊接机器人领域具有设计经验、以及具有多年现场实践经验的相关设计、测试、操作人员组成评价小组，对评价因素进行打分。根据专家自身的权重值bik和各项评价因素的权重值wij，专家k在第i项评价因素上的得分为：

式中：i表示项目因素序列，i＝1,2,3,4；j表示各项因素的级别序列，j＝1,2,3,4,5；

k表示专家的序列，k＝1,2,3,4,5；

将专家k的观点重要度进行归一化处理，即得专家k的权重rk表达式为：

wi表示第i个项目的评分；

(6.3)专家评分

(6.4)建立焊接机器人系统评分系数ωi求解模型。

①求焊接机器人系统评分系数ωi的过程就是求n个模糊数的模糊权重算术平均值的过程。模糊权重算术平均值的计算公式为下式(5)：

式中：代表n个待定权重的模糊数；代表n个模糊数的模糊权重；

设分别为子系统i关于复杂度、工作时间等四个评价因素的模糊评定等级,分别为专家组成员j给出的关于复杂度、工作时间等四个评价因素的模糊权重，为m个专家成员的相对权重，则各分系统的模糊评分系数求解模型为：

通过式(6)～(9)可计算得到各分系统复杂度、技术水平、工作时间、环境条件的总体模糊评价也可以由式(10)—(13)得到专家成员所给出各评价因素的模糊权重

评价因素的模糊权重算数平均值可由式(5)计算得到下式：

对式(14)进行变换，并利用λ截集和zadeh展开理论，可得下式：

min:

s.t.μ1+μ2+μ3+μ4＝1

z≥0

max:

s.t.μ1+μ2+μ3+μ4＝1

z≥0

令为模型(15)、(17)的最优解，即和利用设定不同的λ截集求其并集，它的表达式为：

②模糊加权平均值的最后结果也是一个模糊值，并不是我们需要的最终结果。因此，需要对其结果进行去模糊化处理。去模糊化的实质就是模糊化的逆运算，它是指将模糊演绎过程中得到的模糊值转化成一个与之相对应单一清晰数值的过程。目前，去模糊化的方法有多种，其中最受欢迎的质心法。

利用质心法对模糊集合进行去模糊化处理，其中定义为去模糊化后模糊集所对应的准确值，则：

其中定义为去模糊化后模糊集所对应的准确值；代表n个待定权重的模糊数；代表n个模糊数的模糊权重；a,d代表上下边界；u代表去模糊权重系数，μ1+μ2+μ3+μ4＝1；

当模糊集由其λ截集表示时，则：

代表模糊集，λ截集代表系统内某个元器件的工作故障率；l和h代表评定因素语言模糊变量的上下界；u代表并集运算处理；

计算下式(24)、(25)，并将计算结果带入等式(20)即可求出模糊集合去模糊化后的清晰值。

当△λi＝1/n，并且λi＝i/n,i＝0,1,2,…,n时，等式(22)(23)可简化为：

步骤7，确定焊接机器人系统的mtbf值：由步骤6可以得到各子系统的的评分系数，然后以控制子系统的mtbf为基准，即可得到其他子系统的mtbf值，最后根据步骤3建立的可靠性数学模型即可确定焊接机器人系统的mtbf值。

本发明引入模糊理论对影响焊接机器人系统可靠性的重要度、工作时间等因素进行了三角函数模糊化处理，并考虑了评价因素的权重，采用层次分析法确定了专家权重。利用λ截集的zadeh扩展理论求解若干个模糊数的模糊权重平均值，最后运用质心法进行去模糊化处理，得到了焊接机器人各子系统的评分系数。不需要对焊接机器人系统的机械零部件进行可靠性预计就可以最终确定焊接机器人系统的mtbf值。该发明既能减少元器件计数法对可靠性数据收集的时间又能克服传统专家评分法的弊端。

实施例1

以下结合附图和实施例对本发明作进一步说明。

结合图1～图4，基于焊接机器人系统层次划分的可靠性模糊预计方法的具体实施步骤如下：

步骤1，根据pr1400焊接机器人系统组成及其功能进行层次划分。

1.2详细了解pr1400焊接机器人系统的结构及零部件组成。pr1400焊接机器人系统简化后如图1所示：

1.3根据pr1400焊接机器人的组成结构以及所实现的功能进行层次划分，将焊接机器人系统抽象成控制子系统，焊接子系统、本体子系统三个子系统。焊接机器人系统的层次划分结果如图2所示，各子系统的组成部分如下：

(一)机器人的本体子系统

通常包括基座、肩关节、下臂、上臂、手腕等关键结构。

(二)机器人的控制子系统

包括硬件系统、和软件系统。例如：伺服驱动器、变压器、集成电路板、可编程逻辑控制器、供电回路单元、滤波器、传感器、示教器等。

(三)机器人的焊接子系统

包括焊接电源、送丝机、焊枪、清枪站等组成同时根据子系统的划分编制相应的焊接机器人系统代码表如下表1所示。

表1

步骤2，建立pr1400焊接机器人系统以及控制子系统的可靠性框图。如图3、4所示。

步骤3，构建pr1400焊接机器人系统以及控制子系统的可靠性数学模型。

3.1通过图3pr1400焊接机器人系统整体可靠性框图可知，整个机器人系统可以由三个简化的子系统彼此串联而成，它的可靠性模型为：

r(t)＝rr(t)×rc(t)×rw(t)(1)

式(1)中：r(t)为系统的可靠度，rr(t)、rc(t)、rw(t)分别为pr1400焊接机器人的本体子系统、控制子系统、焊接子系统的可靠度。

3.2同理，对于单个串联的子系统而言，其可靠度可根据组成子系统的零部件的故障率求出，如果各零部件之间的连接是通过串联建立的，那么子系统的故障率可以使用各零部件故障率相乘得出。机器人的子系统可靠度计算公式如下：

rs(t)＝r1(t)×r2(t)×r3(t)×......×rn(t)(2)

式(2)中：rs(t)为机器人子系统的可靠度；ri(t)为第i个串联的零件可靠度。

因此，根据上述方法建立了整机-子系统层面的pr1400焊接机器人可靠性框图及其数学模型。同时可以根据整机-子系统框图和模型建立子系统-零部件层面的可靠性框图及其数学模型。

步骤4，确定pr1400焊接机器人控制子系统的失效率。

根据控制子系统的元器件组成，参考gjb/z299《电子设备可靠性预计手册》中所提供的数学模型，假设焊接机器人系统中所有零部件的密度函数类型都呈指数分布，根据控制子系统的可靠性数学模型，经过大量统计分析和数学计算，得到pr1400焊接机器人控制子系统的失效率，也即控制子系统的mtbf值。控制子系统的可靠性预计结果如表2所示。

表2

表4.3(续)

从上表中可以得出pr1400焊接机器人控制子系统的失效率为λc＝9.6201e-5(1/h)。

步骤5，确定pr1400焊接机器人系统可靠性预计的影响因素。

影响焊接机器人可靠性的因素很多，在实际工程中通常考虑的可靠性因素有复杂程度、工作时间、技术水平、环境条件等。

步骤6，确定各子系统的评分系数。

6.1建立机器人系统的评分因素模糊语言集。

用确定值来表达评价因素误差较大，需要采用有一定变化范围的模糊区间来评定。表3给定了pr1400焊接机器人系统可靠性评价因素的等级评价标准。

表3

各评价因素等级以及相对重要性模糊数如下表4所示。

表4

6.2确定专家权重。

邀请在焊接机器人领域具有设计经验、以及具有多年现场实践经验的相关设计、测试、操作人员组成评价小组，对评价因素进行打分。根据专家自身的权重值和各项评价因素的权重值，专家k在第i项评价因素上的得分为：

式中：i表示项目因素序列，i＝1,2,3,4；j表示各项因素的级别序列，j＝1,2,3,4,5；k表示专家的序列，k＝1,2,3,4,5。

将专家k的观点重要度进行归一化处理，即得专家k的权重表达式为：

通过式(4.19)和(4.20)计算得各专家权重如下表5所示。

表5

6.3专家打分。

邀请研发部与测试部的相关专家对影响pr1400焊接机器人三个子系统的可靠性影响因素进行分别打分可得到专家评分表6和评分因素权重及专家权重表7。

表6

表7

6.4建立pr1400焊接机器人系统评分系数ωi求解模型。

6.4.1求pr1400焊接机器人系统评分系数ωi的过程就是求n个模糊数的模糊权重算术平均值的过程。模糊权重算术平均值的计算公式为下式(5)。

式中：代表n个待定权重的模糊数；代表n个模糊数的模糊权重。

6.4.2设分别为子系统i关于复杂度、工作时间等四个评价因素的模糊评定等级,分别为专家组成员j所给出的关于复杂度、工作时间等四个评价因素的模糊权重，为m个专家成员的相对权重，则各分系统的模糊评分系数求解模型为：

根据式(6)—(13)对表6和7进行计算可得到评价因素及其权重度评价信息统计表8。

表8

评价因素的模糊权重算数平均值可由式(5)计算得到下式：

对式(14)进行变换，并利用λ截集和zadeh展开理论，可得下式：

min:

s.t.μ1+μ2+μ3+μ4＝1

z≥0

max:

s.t.μ1+μ2+μ3+μ4＝1

z≥0

令为模型(15)、(17)的最优解，即和利用设定不同的λ截集求其并集，它的表达式为：

给定λ的值取，可建立六个等差数列的各分系统复杂度、环境条件、工作时间、技术水平的λ截集，如下表9所示。

表9

根据模糊数的计算值和λ水平的设定，建立评价因素复杂度、技术水平、工作时间、环境条件的模糊权重度λ截集，如表10所示。

表10

根据各分系统评价因素及其权重度λ截集的计算结果，按照式(15)、(16)、(17)、(18)计算各分系统模糊评分系数的λ截集，如表11所示。

表11

6.4.3去模糊化

模糊加权平均值的最后结果也是一个模糊值，并不是我们需要的最终结果。因此，需要对其结果进行去模糊化处理。去模糊化的实质就是模糊化的逆运算，它是指将模糊演绎过程中得到的模糊值转化成一个与之相对应单一清晰数值的过程。目前，去模糊化的方法有多种，其中最受欢迎的质心法。

利用质心法对模糊集合进行去模糊化处理，其中定义为去模糊化后模糊集所对应的准确值，则：

当模糊集由其λ截集表示时，则：

计算下式(24)、(25)，并将计算结果带入等式(4.13)即可求出模糊集合去模糊化后的清晰值。

当并且λi＝i/n,i＝0,1,2,…,n时，等式(4.15)(4.16)可简化为：

利用式(20)、(24)、(25)将表11进行去模糊化，得出模糊评分系数的质心值，然后将控制子系统的评分数设为1，并以其为基准，计算其他各子系统评分系数。根据之前元器件计数法的结果可知，焊接机器人的控制子系统故障率为λc＝9.6201e-5/h。从而得到各分系统的故障率，如表12所示。

表12pr1400焊接机器人系统故障率表

步骤7，确定焊接机器人系统的mtbf值。

根据表4.14可知pr1400焊接机器人系统整体的失效率为λs＝9.6201e-5+8.9774e-5+7.9529e-5＝2.6550e-4(1/h)。所以pr1400焊接机器人系统的平均无故障间隔时间mtbf＝1/λs＝3766(h)。