一种协作机器人实时避障方法与流程

本发明涉及机器人控制领域，具体涉及一种协作机器人实时避障方法。

背景技术：

随着科技的发展，以协作机器人为代表的新一代机器人已广泛应用于工业、农业、医疗、陪伴等领域。区别于传统工业机器人，协作机器人与人类共存于同一个空间内，因此机器人必须有良好的实时避障能力，能够实现复杂多边环境下对静、动态障碍物的实时躲避，保障人机安全。目前大部分针对机器人的避障算法多集中于移动机器人，由于机械臂的结构更加复杂，在避障过程中必须考虑整个本体的避障问题，其算法设计难度大大增加，传统应用于移动机器人的避障算法难以应用于机械臂系统。

目前针对机械臂的避障方法多基于人工势场法，其中机器人的目标位置对末端执行器产生一个类似引力的作用，同时障碍物对机器人产生类似斥力的作用。但是该类方法一般存在局部极小值问题。而且针对协作机器人这类具有冗余自由度的机械臂而言，并没有针对其自由度冗余特性设计避障策略。

技术实现要素：

本发明的目的在于克服上述现有技术的不足，提供一种协作机器人实时避障方法，可适用于具有冗余自由度的机械臂。

为实现上述目的，本发明的技术方案是：

一种协作机器人实时避障方法，包括：

在机械臂的本体各连杆上均匀选取一组关键点ai，并定义一个半径d1，使以点ai为球心、d1为半径的一系列球体组成的集合a＝{ai|i＝1,...,a}能够完全包围机械臂的本体；

获取障碍物位置的图像信息，并将所获取到的机械臂和障碍物位置图像简化为关键点bj，使以点bj为球心、d2为半径的一系列球体组成的集合b＝{bi|i＝1,...,b}能够完全包围障碍物；

构造描述机器人实时避障的不等式描述|aibj|≥d，其中d＝d1+d2+δd，δd＞0为距离余量，并将不等式描述改写为速度层的不等式描述：

定义d＝|aibj|-d，速度层的不等式为：

其中是的单位向量；jai为机械臂上关键点ai对应的雅克比矩阵，jai是机械臂关节角度θ的函数；g(|d|)是一个k类函数；

选取速度最小范数为冗余度解析方案，优化关节角速度范数

令xd(t)、分别为期望的位置与速度，x(t)为机械臂末端执行器当前的位置，使机械臂的关节角速度满足下式，以使得机械臂的末端执行按照预设的轨迹运行

其中，j(θ)为机械臂的雅克比矩阵，k为正常数，θ，分别为机械臂的关节角度与角速度；

构建机械臂的避障问题建模为：

θmin≤θ(t)≤θmax(3d)

其中，b＝[b11,…,b1a,…,bb1,…,bba]^t∈^ab，θmin，分别为机械臂关节角度与角速度的下界与上界；

对机械臂的的避障问题模型进行优化求解，得到机器人机械臂的关节角速度控制量，并发送给机械臂控制器，控制机械臂实现对障碍物的躲避。

本发明与现有技术相比，其有益效果在于：

1.本方法是实时避障的方法，不需要进行离线规划；

2.所提出的避障算法能够实现对静态、动态障碍物的避障，同时不影响其末端执行器需要执行的操作，两者并行进行，并不矛盾；

3.所提出的避障算法能够同时避免机械臂的物理超限，即关节角度、角速度均不超过其实际限制；

4.所提出的函数g(|d|)是一类函数而非某个特定函数，可以根据实际情况进行选取，有较好的灵活性。

附图说明

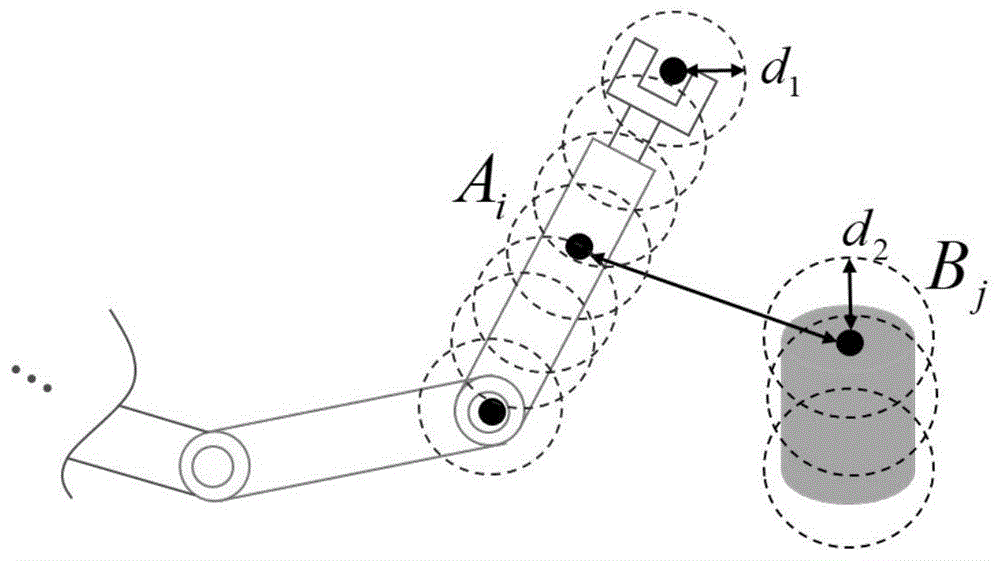
图1为机械臂避障机制示意图；

图2为平面四自由度机器人的原理图；

图3a-3d为机械臂对动态障碍物的躲避情况图；

图4a-4d为仿真曲线图。

具体实施方式

下面结合附图和具体实施方式对本发明的内容做进一步详细说明。

实施例：

本实施例提供的协作机器人实时避障方法主要包括如下步骤：

(一)避障模型构建

机械臂对障碍物的躲避示意图如图1所示。由于机械臂的机构信息一致，可以通过在机械臂的本体各连杆上均匀选取一组关键点ai，并定义一个半径d1，使以点ai为球心、d1为半径的一系列球体组成的集合能够完全包围机械臂的本体；如图1左侧所示；同理，通过获取避障物的图像信息，选取一组bj和半径d2来包裹障碍物；为了避免碰撞，选取一定的余量δd＞0，并定义安全距离d＝d1+d2+δd，在机器人工作过程中，如果使所有的ai和bj均能够使|aibj|≥d，则能够避免碰撞。

(二)将不等式|aibj|≥d描述到速度层：

定义d＝|aibj|-d，速度层的不等式为：

其中是的单位向量；jai为机械臂上关键点ai对应的雅克比矩阵，jai是机械臂关节角度θ的函数；g(|d|)是一个k类函数，是指实数集。

(三)定义最小速度范数为冗余度解析方案

设置一个优化指标为来描述机械臂的能耗情况，若机械臂的速度越大，该值越大，能耗越大，反之则越小。

(四)设计机械臂的运动控制器：

令xd(t)、分别为机械臂末端执行器期望的位置与速度，x(t)为末端执行器当前的位置，设计pd控制器如下，即使机械臂的关节角速度满足下式，则可以使机械臂的末端执行能够按照预设的轨迹运行

其中，j(θ)为机械臂的雅克比矩阵，k为正常数，θ，分别为机械臂的关节角度与角速度。

(五)对机械臂的物理约束进行建模

主要包括关节角度限幅和角速度限幅。定义θmin，分别为机械臂关节角度与角速度的下界与上界，那么该物理约束写为：θmin≤θ(t)≤θmax，

(六)综合考虑步骤二至五，将机械臂的避障问题建模为：

θmin≤θ(t)≤θmax(3d)

其中b＝[b11,…,b1a,…,bb1,…,bba]^t∈^ab，是指实数集。

(七)采用如下的递归神经网络实时计算控制量(即关节的角速度指令)：

其中，ò＞0。λ1∈^m,λ2∈^ab为对偶变量。的计算方法为：对其中的每一行元素，若该元素大于零，则不做修改，若该元素小于0，则令其为0，是指实数集。

将求解得到机器人机械臂的关节角速度控制量发送给机械臂控制器，控制机械臂实现对障碍物的躲避。

在实际应用的过程中，由于本方法主要是在机械臂控制器上进行的，主要包括两个阶段：

初始化阶段：

先初始化控制器参数k，α，ò；获取提前设定的机械臂关键点信息ai，以及其对应的雅克比矩阵jai的表达式；障碍物的关键点bi，安全距离d。预设的机械臂末端任务信息：xd(t)、初始化对偶变量λ1(0)＝0，λ2(0)＝0，机械臂物理约束：θmin，θmax，

算法流程：

1.利用相机等测量单元实时测量障碍物bi的位置信息，并计算其实时速度；

2.读取机械臂当前状态信息：θ，

3.利用θ计算关键点ai对应的位置，计算jo和b；并根据式(4c)更新λ2

4.获取机械臂末端执行器的实时位置x，并根据式(4b)更新λ1

5.根据式(4a)计算关节角速度(即控制指令)。

下面结合一个仿真实例来对本方法进行进一步的验证说明：

选取一个平面四自由度机器人，如图2所示。左侧给出了机械臂的基本结构与关键点的选取方法。其中a1、a3、a5、a7分别位于机械臂各连杆的中心，a2、a4、a6位于关节处。右侧给出了机械臂的d-h参数表。

控制器参数选取如下：ò＝0.001，α＝8，k＝8，d＝0.1m。物理约束为：θmin＝-3rad，θmax＝3rad，k类函数选取为g(|d|)＝500|d|，“ò”表示一个正的控制增益；

定义机器人的末端任务轨迹为：xd＝[0.4+0.1cos(0.5t),0.4+0.1sin(0.5t)]^t

仿真时长20s，其间一个动态障碍物在平面中的运动轨迹为：b＝[-0.1+0.01t,0.3]^t，

障碍物半径为0.05m。仿真结果如图3,4。图3a-d为机械臂对动态障碍物的躲避情况，其中黑色轨迹(大圈)为末端执行器的估计，表明机械臂能够实现对给定任务的操作，小圈为障碍物，表明机械臂能够实现对动态障碍物的实时躲避。图4为仿真曲线：(a)末端执行器对期望轨迹的跟踪误差，可知本专利所提方法能够使末端执行能完成给定任务；(b)关键点与障碍物的距离，可知能够过程中，机械臂与动态障碍物的距离始终不小于预设的安全距离d＝0.1。(c)机械臂的关节角速度曲线(d)机械臂的关节角曲线。图(c)(d)表明在整个过程中机械臂没有超过物理极限

由此可知，本方法提出的避障策略能够在完成末端给定任务的同时实现对障碍物的实时躲避，同时能够避免物理极限。

上述实施例只是为了说明本发明的技术构思及特点，其目的是在于让本领域内的普通技术人员能够了解本发明的内容并据以实施，并不能以此限制本发明的保护范围。凡是根据本发明内容的实质所做出的等效的变化或修饰，都应涵盖在本发明的保护范围内。