四足机器人在负载突变下基于ZMP理论的反应式鲁棒控制方法与流程

本发明属于机器人控制技术，具体为一种四足机器人在负载突变下基于zmp理论的反应式鲁棒控制方法。

背景技术：

在波士顿动力研发出bigdog后，四足机器人受到了来自越来越多研究界的关注。与传统的轮式和履带式机器人不同的是，四足机器人行走时与地面的接触是点式的，所以可以在崎岖不平的山路、泥沼或阶梯等复杂恶劣的环境下移动，且在移动速度、负载能力、稳定性等方面表现出诸多优势。四足机器人在实际环境中往往会面对各种各样复杂的情况，当四足机器人受到负载突变扰动时，机身高度降低，机身姿态倾斜，影响机器人的行走稳定性，严重的时候甚至会造成机身的倾覆，其鲁棒控制问题比较复杂，至今仍没有有效的控制方法被提出。

技术实现要素：

本发明的目的在于提出了一种四足机器人在负载突变下基于zmp理论的反应式鲁棒控制方法，以保证机器人的稳定行走。

实现本发明的技术解决方案为：一种四足机器人在负载突变下基于zmp理论的反应式鲁棒控制方法，具体步骤为：

步骤1、建立四足机器人带扰动项的腿部动力学模型和机身动力学模型，通过机身与四条腿的耦合点，将腿部动力学模型和机身动力学模型结合起来，建立带有扰动项的完整四足机器人动力学模型；

步骤2、根据步骤1中的机身动力学模型确定负载突变下zmp的计算公式；

步骤3、基于zmp规划出四足机器人在负载突变过程中的稳定对角小跑步态；并根据规划出的稳定对角小跑步态，通过逆运动学计算出期望关节角；

步骤4、根据期望关节角，设计带有非线性干扰观测器的滑模跟踪控制器，观测器观测出干扰值，通过滑模控制对干扰进行补偿，实现关节的跟踪控制。

优选地，步骤1建立的四足机器人带扰动项的单腿动力学模型为：

其中，是关节角度向量，是对称半正定惯性矩阵，是向心力和科氏力项，是重力项，是关节力矩，是扰动力矩，是足端接触力雅克比矩阵，是足端和地面的接触力向量，是腿部和机身的耦合点到关节空间的雅克比矩阵，是腿部和机身接触点的耦合力，若单腿处于摆动相时地面接触力fg等于零。

优选地，步骤1建立的四足机器人机身动力学模型为：

其中，表示身体的位置/姿态矢量，为广义力矢量，为对称半正定惯性矩阵，为科氏力和向心力矩阵，为重力矢量。

优选地，步骤1建立的带有扰动项的完整四足机器人动力学模型为：

将定义为其中joi(xo)是从机身坐标系到第i条腿关节1的雅可比矩阵，令l＝jo⁺(xo)je(q)，则上述模型中的参数为：

优选地，步骤2中四足机器人在负载突变下的机身动力学等价为：

其中，m代表机身的质量，θ是机身的惯性张量，g是重力向量，fext和text是负载突变下作用在com处的合力和合力矩，a和ω分别是com的线性加速度和角加速度，所有变量的上标中，坐标系i是惯性坐标系，坐标系b是机身坐标系。

优选地，根据负载突变下的机身动力学确定如下关系：

其中，rib是欧拉旋转矩阵从惯性坐标系到机身坐标系，r和rzmp是com和zmp的位置；

使惯性坐标系的z轴和平面法向量的方向重合，得到负载突变下zmp在x和y上的计算公式为：

其中，zb是rⁱ在z轴上的分量，^xy(·)指一个量在某个平面的分量，^xyl由下式给出：

其中，rib,i指rib的第i行元素。

优选地，步骤3中基于zmp规划出四足机器人在负载突变过程中的稳定步态，具体步骤如下：

步骤31、计算足端支撑线，具体为

机器人的四条腿从左前、右前、左后、右后腿分别编号为1到4，第i条腿足端与地面接触点piⁱ的位置为(xi,yi,zi)(i＝1,...4)，假设下一次足端落地点pi^i′坐标为(xi+δx,yi,zi)，即piⁱ沿着惯性坐标系x轴平移了δx，zi为机身com距离地面的高度，变化后的足端支撑线在xy平面表示为：

步骤32、根据点在直线上定理，求解位移量，具体为：

将zmp的坐标代入足端支撑线方程，如下式：

解得位移量：

步骤33、根据位移量，优化足端轨迹与落足点，具体为：

假设足端落地点pi(xi+δx1,yi+δy1,zi)既沿着机身坐标系x轴方向平移了δx1，又沿着y轴方向平移了δy1，则由几何关系，有以下关系：

δx1＝sin²θδx，δy1＝sinθcosθδx。

四足机器人的trot步态对角线上的两条腿步态一致，t是运动周期，s是单腿的步距，h为髋部到足端最低点的距离，h为髋部到足端最高点的距离，δx1和δy1是基于zmp的调整量，规划出的足端落地点都能符合机器人腿部本身的运动学约束，只要通过规划出足端下一次的落地点pi′的位置(xi+δx1,yi+δy1,zi)，就能使足端落地后，机器人的zmp落在支撑线上，从而保证机器人的稳定行走，trot步态在三个方向上的足端轨迹如下：

优选地，步骤3中的期望关节角为：

其中，l1、l2、l3为四足机器人单腿连杆1、连杆2和连杆3的长度，b＝-2xtrotl2，

优选地，步骤4根据期望关节角，设计带有非线性干扰观测器的滑模跟踪控制器，观测器观测出干扰值，通过滑模控制对干扰进行补偿，实现关节的跟踪控制具体过程如下：

步骤41、设计非线性干扰观测器，具体为：

步骤42、通过线性矩阵不等式求解非线性干扰观测器的增益矩阵x，具体为：

令y＝x^-1，根据schur补定理，lmi求解式为：

其中，ζ为的上界，γ为一个对称正定矩阵，x＝y^-1。

步骤43、设计带有扰动补偿的滑模控制器，具体为：

令λ＝λ1i12×12，定义滑模函数为：

假设关节的期望输入角度为qd，定义跟踪误差e＝q-qd，取辅助变量即有设计的带有扰动补偿的滑模控制器为：

其中，k＝λ2i12×12。

本发明与现有技术相比，其显著优点为：本发明对负载突变这一特定扰动具有较强的针对性，使得四足机器人在负载突变下，能恢复平衡并且继续平稳的以trot步态行走，控制策略有较强鲁棒性。

下面结合附图对本发明做进一步详细的描述。

附图说明

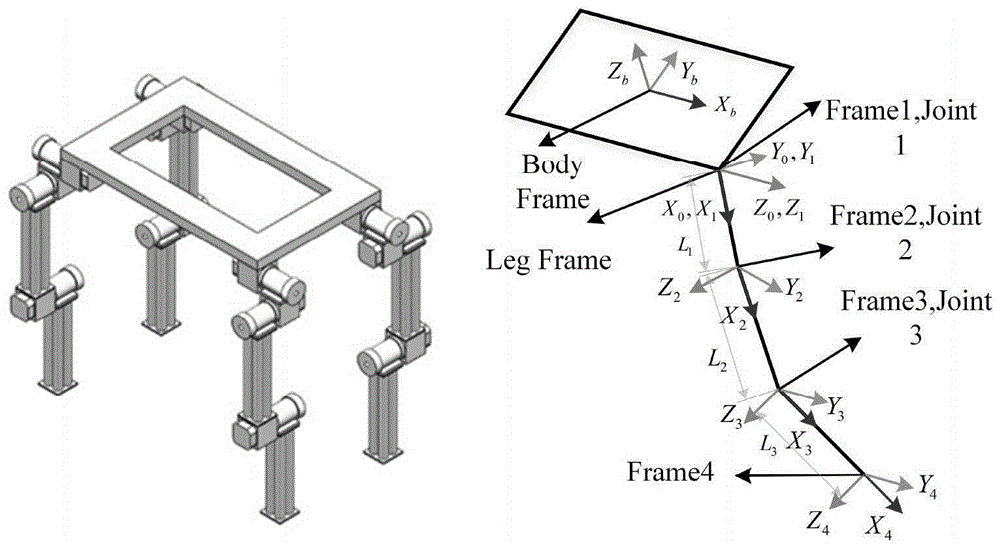
图1是四足机器人结构和单腿坐标系。

图2是控制系统方案的结构框图。

图3是δx分解为δx1和δy1示意图。蓝色的点是足端触地点，红色的点是zmp，θ是足端支撑线和机器人前进方向的夹角。

图4是三种控制策略下机器人横滚角的绝对值曲线。

图5是三种控制策略下机器人俯仰角的绝对值曲线。

图6是机器人关节1期望角度和实际跟踪曲线。

图7是机器人关节2期望角度和实际跟踪曲线。

图8是机器人关节3期望角度和实际跟踪曲线。

图9是matlab和adams联合仿真中的机器人虚拟样机截图。

具体实施方式

一种四足机器人在负载突变下基于零力矩点(zeromomentpoint，zmp)理论的反应式鲁棒控制方法，具体步骤为：

步骤1、建立带扰动项的四足机器人完整动力学模型；

如图1，考虑四足机器人的每条腿有三个自由度，机器人突加负载时候受到的外力扰动可以部分折算到关节上的扰动力矩，带有扰动项的第i条腿(i＝1,...k)的动力学模型可以描述为：

其中，是关节角度向量，是对称半正定惯性矩阵，是向心力和科氏力项，是重力项，是关节力矩，是扰动力矩，是足端接触力雅克比矩阵，是足端和地面的接触力向量，是腿部和机身的耦合点到关节空间的雅克比矩阵，是腿部和机身接触点的耦合力，若单腿处于摆动相时地面接触力fg等于零。

所有腿的动力学可以表示为：

其中，

令l1、l2、l3为四足机器人单腿连杆1、连杆2和连杆3的长度，m1、m2、m3为连杆1、连杆2、连杆3的质量。模型具体参数如下：

j12＝l2cosθi2+l3cos(θi2+θi3)

j13＝l3cos(θi2+θi3)

j21＝cosθi1(l1+l2cosθi2+l3cos(θi2+θi3))

j22＝-sinθi1(l2sinθi2+l3sin(θi2+θi3))

j23＝-l3sinθi1sin(θi2+θi3)

j31＝sinθi1(l1+l2cosθi2+l3cos(θi2+θi3))

j32＝cosθi1(l2sinθi2+l3sin(θi2+θi3))

j23＝l3cosθi1sin(θi2+θi3)

用表示身体的位置/姿态矢量，四足机器人机身的动力学方程由作用在机身质心(com)的广义力矢量包括机器人负载突变下作用在com处的合外力和合外力矩，对称半正定惯性矩阵科氏力和向心力矩阵以及重力矢量组成。机身动力学方程描述为：

机身动力学的具体参数如下：

gb＝[00-mg000]^t其中，mφ＝a^tiba，ib是机身质心的转动惯量，m是机身质量，其中φb＝[φx,φy,φz]^t分别代表了机身的横滚，俯仰，偏航角。

将定义为其中joi(xo)是从机身坐标系到第i条腿关节1的雅可比矩阵。由相互作用力可知，fo可写为：

fo＝-jo^t(xo)fe(1.4)

由式(1.4)可知，腿部支撑力fe可表示为：

fe＝-jo^t(xo)⁺fo(1.5)

其中是jo^t(xo)的伪逆矩阵。将(1.5)代入(1.2)，我们得到

令为机身与第i条腿的耦合点的位置矢量。由雅可比矩阵jei(qi)可以得到xie与qi的关系为：

同理，与的关系为：

结合(1.7)和(1.8)，可以获得第i条腿的关节速度与机身位姿速度之间的关系：

假设腿工作空间足够合理以保证雅可比矩阵jei(qi)存在逆矩阵。考虑所有腿同时作用在机身，可以得到：

式(1.10)关于时间t求微分得到：

将式(1.10)和(1.11)代入到式(1.3)得到：

令l＝jo⁺(xo)je(q)，则在式(1.12)两边均左乘l^t，得到：

将式(1.13)和式(1.6)合并，可以得到完整的动力学方程为：

其中：

步骤2、结合机身动力学推导出负载突变下zmp的计算公式；

从运动学角度来看，负载突变主要影响四足机器人机身的高度和机身在空间中的姿态。若从动力学角度看，负载突变作用于机身可以分解为扰动力和力矩。将机身动力学信息引入zmp判据中来，结合四足机器人动力学模型，式(1.3)中机器人在负载突变下的机身动力学同样可以描述为：

其中，m代表机身的质量，θ是机身的惯性张量，g是重力向量，fext和text是负载突变下作用在com处的合力和合力矩，a和ω分别是com的线性加速度和角加速度。所有变量的上标中，坐标系i是惯性坐标系，坐标系b是机身坐标系。

在一个平整的路面上，zmp被定义为由重力和惯性力合力投影到地面上的点。假设地面平面的法向量nⁱ，结合式(2.1)，可以得到以下关系：

其中，rib是欧拉旋转矩阵从惯性坐标系到机身坐标系，r和rzmp是com和zmp的位置。使惯性坐标系的z轴和平面法向量的方向重合，式(2.2)中zmp在x和y上的分量可以得出

其中，zb是rⁱ在z轴上的分量，^xy(·)指一个量在某个平面的分量，^xyl由下式给出

其中，rib,i指rib的第i行。

步骤3、基于zmp规划出四足机器人在负载突变过程中的稳定的步态；

步骤31、trot步态设计；

步态是各腿在时间和空间上的运动顺序，平整地面上多为周期步态。当腿与地面接触时，腿的状态为支撑相，腿在空中摆动时状态为摆动相。对角小跑步态(trot)是稳定性极高的动步态，其对角线上的腿运动一致。

对角小跑步态占空比为0.5，即每个时刻都有两条腿处于着地状态，另外两条腿处于空中摆动状态。

trot步态时，对角线上两足运动状态一致，支撑相两足相对于各自髋部的速度是一致的，足端轨迹采用多项式形式，四足机器人单腿摆动相轨迹如下：

其中，t是运动周期，s是单腿的步距，h为髋部到足端最低点的距离，h为髋部到足端最高点的距离

步骤32、基于zmp稳定判据的落地点选择；

四足机器人处于trot步态时，只有两条腿同时接触地面，构成支撑线。只有当zmp点落在这条支撑线上，才可以认为此时机器人现在处于行走稳定状态。

机器人的四条腿从左前、右前、左后、右后腿分别编号为1到4，第i条腿足端与地面接触点piⁱ的位置为(xi,yi,zi)(i＝1,...4)。假设下一次足端落地点pi^i′坐标为(xi+δx,yi,zi)，即piⁱ沿着惯性坐标系x轴平移了δx。因为在行走过程中zmp和机器人足端支撑线都在地面，所以zi就是机身com距离地面的高度。变化后的足端支撑线在xy平面可以表示为式

根据trot步态的相位关系可知，i＝1时j＝4，或i＝2时j＝3。

为了使zmp落在机器人的支撑线上，根据点与直线的判断条件，将zmp的坐标代入支撑线方程，如下式

解得

这样，就可以计算出δx的值，从而使zmp点落在支撑线上。但上述过程明显存在不足，那就是只需要调节落地点x轴方向上的位置，实际的trot步态中，需要从x和y方向一起来调节足端落地点。假设足端落地点pi(xi+δx1,yi+δy1,zi)既沿着机身坐标系x轴方向平移了δx1，又沿着y轴方向平移了δy1，如图2(b)。图2的几何关系可以得出：

δx1＝sin²θδx(3.7)

δy1＝sinθcosθδx(3.8)

假设规划出的足端落地点都能符合机器人腿部本身的运动学约束，只要通过规划出足端下一次的落地点pi′的位置(xi+δx1,yi+δy1,zi)，就能使足端落地后，机器人的zmp在支撑线上，基于zmp四足机器人负载突变下稳定的trot步态轨迹为：

步骤33四足机器人逆运动学

根据机器人的d-h坐标系建立规则，建立四足机器人各足在机器人质心坐标系下的位置与各关节角度的关系模型。四足机器人各条腿的d-h坐标系如图1所示。通过齐次坐标变换可以得到第i条腿足端位置和关节角度关系如下：

若已知足端规划的轨迹，通过联立上面三个方程，可以通过逆运动学解出三个关节的期望角度：

其中，b＝-2xtrotl2，

步骤4、设计非线性干扰观测器，利用观测器测出的干扰值，通过滑模控制对干扰进行补偿，实现关节角的跟踪控制；

提出了一种基于非线性干扰观测器的滑模角度跟踪控制策略。图3描述了用于抑制扰动的非线性干扰观测器和计算力矩法的滑模控制的结构框图。四足机器人先规划好步态，给出关节期望的角度与角速度。再根据与实际关节角度跟踪的误差，建立了一个滑模面。然后通过非线性干扰观测器尽可能的估计关节上存在的扰动，通过滑模补偿，来抵消扰动或者尽可能降低扰动带来的影响。最后基于zmp修正并规划出下一周期的步态。

步骤41、干扰观测器的设计与稳定性分析

非线性干扰观测器(nonlineardisturbanceobserver，nldo)设计为

干扰观测器的增益矩阵取

其中，x∈r^3k×3k是一个常数可逆的矩阵。

由于角加速度信号的难以获得，向量可以由改进的观测器增益矩阵l(q)得到：

结合式(4.2)和(4.3)，可得：

从而，式(4.1)、(4.2)和(4.4)构成了完整的非线性干扰观测器。

设计李雅普诺夫函数

由于为对称正定矩阵，x也是可逆矩阵，所以推出也是正定的。从而李雅普诺夫函数v0也是正定的。观测误差定义为

取式(4.5)对时间的导数，得到

由观测器式(4.1)可得

假设干扰力矩d为常值扰动，则有在机器人学的文献中，这样的假设很常见。因而可以通过式(4.7)得到观测误差方程为

这等价于：

将式(4.9)代入式(4.6)，得到

假设存在一个对称正定的矩阵γ满足如下不等式：

于是

由式(4.10)和(4.11)可知，对于所有的观测误差都负定，即：对于都有

继续考虑李雅普诺夫函数的收敛速度问题，由式(4.5)可以得出：

定义的下确界为σ1，上确界为σ2，则由式(4.13)可以得出如下方程：

同理，由式(4.12)可以得出：

联立(4.14)与(4.15)，得到

所以，李雅普诺夫标量函数v0的最小收敛速率为

由式(4.5)可以得到：

联立式(4.16)、(4.17)，可得：

式(4.18)左右两边同时开根号，就可以得出干扰观测器跟踪信号误差最小收敛速率为λmin(γ)/2σ1||x||²。由此得出，λmin(γ)越大，||x||越小，观测器跟踪误差最小收敛速率越大。

步骤42、lmi不等式的求解；

由不等式(4.11)可见，式中含有非线性项，必须转化为线性矩阵不等式(linearmatrixinequation，lmi)才能求解。令y＝x^-1，将y^t＝(x^-1)^t和y＝x^-1分别乘以式(4.11)的左右两边，得

即

定义的上界为ζ，则可以推出则式(4.20)成立的充分条件为

y^t+y-ζi-y^tγy≥0(4.21)

根据schur补定理，则上式(4.21)等价为

通过matlab下的lmi控制工具箱求解式(4.22)，便可以得到y，从而得到x。

步骤43、计算力矩法的滑模控制器设计

采用观测器式(4.1)观测干扰d，在滑模控制(sliding-modecontrol，smc)中对干扰进行补偿，可有效地降低切换增益，从而有效地降低抖振。

假设关节的期望输入角度为qd，定义跟踪误差e＝q-qd，取辅助变量即有

其中，λ＝λ1i12×12，λ1＞0。定义滑模函数为

于是

设计控制器为

从而有

其中，k＝λ2i12×12，λ2＞0。

由于为正定阵，设计闭环系统lyapunov函数为

由于干扰观测器指数收敛，则取则有

由于为一个反对称矩阵，则有

由上式可得

其中，λkmin和分别为k和的最小和最大特征值。

采用不等式求解式(4.30)，不等式方程的解为

从而可得，当t→∞时，滑模函数s趋近于零，即且指数收敛，收敛速度取决于参数μ的值。

通过本发明提出了一种负载突变情况下的四足机器人反应式鲁棒控制方法，通过计算基于zmp稳定判据的落足点，来保证四足机器人的稳定性，建立如图3所示的控制结构，实现规划腿部运动轨迹的跟踪。负载在仿真第4s坠落撞击到机身。图4、5为三种控制方式对姿态信息的影响，从图中可以看出，采用本发明的基于zmp的反应式鲁棒控制方法，姿态角在扰动影响下变化程度更小，说明机器人稳定性也越好。图6、图7、图8为四足机器人左前腿三关节的期望角度和实际跟踪角度。每个关节期望的角度是通过基于zmp规划出的步态和逆运动学求解出的，关节跟踪控制器采用带有非线性干扰观测器的滑模控制器。从三幅图中可以看出，三个关节角跟踪性能较好，当机器人受到负载突变时，只有关节3的跟踪误差较大，但之后关节迅速跟踪上期望关节角信号。图9通过对负载突变下的四足机器人进行matlab和adams联合仿真，验证了本文所提出的控制策略的有效性。