一种六自由度关节型机器人的奇异性处理方法与流程

本发明涉及一种六自由度关节型机器人的奇异性处理方法。

背景技术：

奇异位形是机器人机构的固有特性，当机器人处于奇异位形时，对于给定操作器的从关节空间映射到工作空间的雅可比矩阵就变为奇异矩阵，因而无法求得它的运动学逆解，从而基于雅可比的各种控制算法就失效了，这样其轨迹控制和运动控制都无法准确实现。以目前常见的六自由度关节型机器人为例，主要包括三种奇异点，分别为边界奇异、内部奇异和腕部奇异。当第二、三和五关节同轴时会出现边界奇异；当第一和第六关节同轴时会出现内部奇异；当第四和第六关节同轴时会出现腕部奇异。这些奇异位形会导致机器人关节速度突然变大，从而导致停机或者其他安全问题。

技术实现要素：

本发明是为了避免现有技术所存在的不足，提供一种六自由度关节型机器人的奇异性处理方法，以期能在保证机器人工作性能和运动精度前提下，提高机器人运动的平稳性，使机器人各关节角度和角速度平稳通过奇异区域。

本发明解决技术问题采用如下技术方案：

本发明一种六自由度关节型机器人的奇异性处理方法的特点是按如下步骤进行：

步骤1、对六自由度关节型机器人进行结构学与运动学分析，建立运动学模型，从而获取运动学正逆解求解公式及雅可比矩阵；

步骤2、对所述六自由度关节型机器人进行笛卡尔空间的运动轨迹规划，得到末端执行器在各个插值点处的位置、速度和加速度；

步骤3、对所述运动轨迹的各个插值点进行运动学逆解求解，得到各插值点处机器人各关节的角度，并根据雅可比矩阵对笛卡尔空间与关节空间的联系，得到各插值点处机器人各关节的角速度和角加速度；

步骤4、求解关节奇异的条件，并得到奇异域；

步骤5、基于所述奇异域的边界上的插值点处机器人各关节的角度、角速度、角加速度，利用五次多项式对奇异域内的所有插值点进行重新规划，得到非奇异域内的插值点，从而与奇异域边界上的插值点组成新的运动轨迹，以使六自由度关节型机器人平稳地通过奇异域。

本发明所述的六自由度关节型机器人的奇异性处理方法的特点也在于，所述步骤5是按如下过程进行：

步骤5.1、将奇异域边界上的始端插值点的角度记为θ0、角速度记为θ′0、角加速度记为θ″0；将奇异域边界上的末端插值点的角度记为θf、角速度记为θ′f、角加速度记为θ″f，并带入五次多项式中，从而求解得到五次多项式的各个系数如式(1)所示：

式(1)中，tf表示末端插值点的时间；

步骤5.2、将奇异域内的所有插值点的时刻带入求解后的五次多项式中，从而得到新的插值点作为非奇异域内的插值点。

与已有技术相比，本发明有益效果体现在：

1、本发明方法简单，可操作性高，便于实现程序化，对扩大机器人的应用范围、提高操作精度、灵活性和运动学及动力学性能都有着十分重要的实际意义。

2、本发明方法通过离线仿真可预先判断工业机器人是否处于奇异位形，并对位于奇异位形内的运动轨迹进行重新规划，与非奇异区域的轨迹组成新的轨迹并写入机器人控制器中，克服了工业机器人在工作过程中遇到奇异位形时出现关节角速度突变而运行不稳定的问题，从而使机器人平稳通过奇异区域。

附图说明

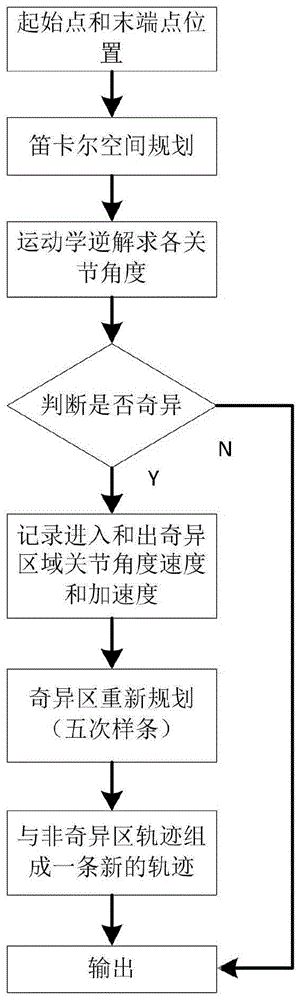
图1为本发明中六自由度奇异性处理方法流程图；

图2为六自由度关节型机器人d-h坐标示意图；

图3a为本发明中未进行奇异性处理前的各关节角度与时间关系图；

图3b为本发明中未进行奇异性处理前的角速度与时间关系图；

图3c为本发明中未进行奇异性处理前的角加速度与时间关系图；

图4a为本发明中进行奇异性处理后的各关节角度与时间关系图；

图4b为本发明中进行奇异性处理后的角速度与时间关系图；

图4c为本发明中进行奇异性处理后的角加速度与时间关系图。

具体实施方式

本实施例中的六自由度关节型机器人是指具有六个旋转关节的工业机器人。如图1所示，一种六自由度关节型机器人的奇异性处理方法是按如下方式进行：

步骤1、对六自由度关节型机器人进行结构学与运动学分析，建立运动学模型，从而获取运动学正逆解求解公式及雅可比矩阵；如图2所示，分别建立六自由度关节型机器人的d-h坐标系；具体为：坐标系原点o为六自由度机器人腰关节、肩关节轴线的公垂线与腰关节轴线的交点，z轴与腰关节轴线重合，方向竖直向上，x轴与腰关节、肩关节轴线的公垂线重合，从腰关节指向肩关节，y轴按右手螺旋法则确定。并且可以用如式(1)所示的六个d-h关节变换矩阵来表示：

式(1)中，为关节轴i相对关节轴i-1的齐次变换矩阵，i＝1、2、3、4、5、6；si为关节角正弦值，且si＝sinθi；ci为关节角余弦值，且ci＝cosθi；θi是两相邻连杆绕公共轴线旋转的夹角，称作关节角；di是两相邻连杆公共轴线方向的距离，称作连杆偏距；ai-1是两个关节轴之间的距离，称作连杆长度；

运动学正解如式(2)所示：

式(2)中，nx为x轴第一旋转参量，ny为x轴第二旋转参量，nz为x轴第三旋转参量，ox为y轴第一旋转参量，oy为y轴第二旋转参量，oz为y轴第三旋转参量，ax为z轴第一旋转参量，ay为z轴第二旋转参量，az为z轴第三旋转参量，px为第一偏移参量，py为第二偏移参量，pz为第三偏移参量，并有：

nx＝s6(s1c4-c1c23s4)-c6[c1s23s5-c5(s1s4-c1c23c4)]；

ny＝-s6(c1c4+s1c23s4)-c6[s1s23s5+c5(c1s4-s1c23c4)]；

nz＝s23s4s6-c6(c23s5+s23c4c5)；

ox＝s6[c1s23s5-c5(s1s4+c1c23c4)]+c6(s1s4-c1c23s4)；

oy＝s6[s1s23s5+c5(c1s4-s1c23c4)]-c6(c1c4+s1c23s4)；

oz＝s6(c23s5+s23c4c5)+s23s4c6；

ax＝-c1s23c5-s5(s1s4+c1c23c4)；

ay＝-s1s23c5+s5(c1s4-s1c23c4)；

az＝s23c4s5-c23c5；

px＝c1(a1+a2c2+a3c23-d4s23)+d6ax；

py＝s1(a1+a2c2+a3c23-d4s23)+d6ay；

pz＝-a2s2-a3s23-d4c23+d6az+d1；

c23＝c2c3-s2s3；s23＝c2s3+s2c3；

运动学逆解如式(3)所示：

式(3)中，k为中间参量1，m为中间参量2，并有：

m＝pxc1+pys1-a1；

利用式(4)得到六自由度关节型机器人雅可比矩阵j(θ)：

式(4)中，j11为第一雅可比块矩阵1，j12为第二雅可比块矩阵，j21为第三雅可比块矩阵，j22为第四雅可比块矩阵，并有：

步骤2、在仿真软件中对六自由度关节型机器人进行笛卡尔空间的运动轨迹规划，得到末端执行器在各个插值点处的位置p、速度v和加速度a；

步骤3、对运动轨迹的各个插值点进行运动学逆解求解，利用式(5)得到各插值点处机器人各关节的角度θi:

根据雅可比矩阵对笛卡尔空间与关节空间的联系，利用式(6)得到各插值点处机器人各关节的角速度和角加速度

步骤4、求解关节奇异的条件，并得到奇异域。当det(j(θ))＝0时，六自由度关节型机器人产生奇异位形，此时求得：

a3s3+d4c4＝0；s5＝0分别为边界奇异、内部奇异和腕部奇异。

利用式(7)分别设置奇异判别因子：

式(7)中，kb为边界奇异判别因子，kn1为第一内部奇异判别因子，kn2为第二内部奇异判别因子，kw为腕部奇异判别因子。

针对三种奇异点分别设置奇异阈值t1、t2、t3。当|kb|＜t1时，六自由度关节型机器人处于边界奇异位形；当|kn1|＜t2|kn2|＜t2时六自由度关节型机器人处于内部奇异位形；当|kw|＜t3时六自由度关节型机器人处于腕部奇异。

步骤5、基于奇异域的边界上的插值点处机器人各关节的角度、角速度、角加速度，利用五次多项式对奇异域内的所有插值点进行重新规划，得到非奇异域内的插值点，从而与奇异域边界上的插值点组成新的运动轨迹，以使六自由度关节型机器人平稳地通过奇异域。

步骤5.1、对原规划轨迹插值点进行运动学逆解求解时，使用奇异性判别条件，若插值点未经过奇异域则正常输出，若插值点进入奇异域，则记录进入奇异域和离开奇异域两个插值点的各关节角位移、角速度和角加速度。将奇异域边界上的始端插值点的角度记为θ0、角速度记为θ′0、角加速度记为θ″0；将奇异域边界上的末端插值点的角度记为θf、角速度记为θ′f、角加速度记为θ″f，并带入五次多项式θ(t)＝a0+a1t+a2t²+a3t³+a4t⁴+a5t⁵中，从而求解得到五次多项式的各个系数如式(8)所示：

式(8)中，tf表示末端插值点的时间。

步骤5.2、将奇异域内的所有插值点的时刻带入求解后的五次多项式中，从而得到新的插值点作为非奇异域内的插值点，与非奇异区域内轨迹组成新的轨迹输出。从而使得机器人平稳通过奇异区域。

实施例1：

当给出机器人运动起始点p1和终点p2，奇异性处理方法按如下步骤进行：

步骤1、利用d-h坐标系建立运动学模型，进行运动学正逆解求解。

步骤2、进行笛卡尔空间轨迹规划，插补周期0.05s，总时间5s。

步骤3、对各个插值点进行运动学逆解求解，求得各个关节角度、角速度和角加速度。

步骤4、利用奇异判别条件，判断插值点是否在奇异区域内，图3a、图3b和图3c为未经奇异性处理前的关节空间轨迹，从图中可以看到机器人各个关节的角度、角速度、角加速度的变化情况，机器人经过腕部奇异位形区域，第四关节速度与第六关节速度产生突变。

步骤5、记录上述步骤中运动轨迹进入奇异区域和出奇异区域时候的角度、角速度、角加速度，利用五次多项式对奇异区域内的轨迹进行重新规划，与非奇异区域内轨迹组成新的轨迹，使机器人平稳通过奇异区域，图4a、图4b和图4c为经奇异性处理后的关节空间轨迹，从图中曲线可以看到机器人顺利通过奇异区域并且保证了运动的连续性，没有出现关节速度突变情况，证明了通过奇异区域轨迹规划算法的正确性和可行性。