一种基于PI控制策略的机械臂柔性关节位姿变换抑振方法与流程

本发明属于机械臂谐振抑制技术领域，尤其涉及一种基于pi控制策略的机械臂柔性关节位姿变换抑振方法。

背景技术：

机械臂广泛应用于工业装配、安全防爆等诸多方面。机械臂是一个多输入多输出、高度非线性、强耦合的复杂系统。对于许多高性能机械臂来说，电机和负载间的传动柔性是一个不可忽略的影响因素。导致这种柔性存在的成因很复杂，既有传动系统中齿轮、联轴器、滚珠丝杠存在的弹性，也有传动轴本身扭转刚度等。这种柔性的存在能够引发机械臂谐振，并且谐振的强弱可通过系统动态响应特性反映。当伺服电机控制器特性与机械环节特性符合一定条件时，系统将出现谐振现象，导致负载端、电机端强烈抖动。这种谐振会影响机械臂的动态精度，甚至损坏机械臂。因此，进行机器人的谐振抑制是非常重要的。

技术实现要素：

(一)要解决的技术问题

针对现有存在的技术问题，本发明提供一种基于pi控制策略的机械臂柔性关节位姿变换抑振方法。

(二)技术方案

为了达到上述目的，本发明采用的主要技术方案包括：

一种基于pi控制策略的机械臂柔性关节位姿变换抑振方法，建立机械臂的柔性关节伺服系统动力学模型，将变参数pi控制策略应用于机械臂的柔性关节伺服系统动力学模型的速度控制中；

其中，变参数pi控制策略的参数根据机械臂柔性关节电机端、负载端的转动惯量随位姿变化来进行调整；

其中，机械臂的柔性关节伺服系统动力学模型的方程表达式为：

式中：jm表示电机转动惯量，θm表示电机转角，jl表示负载转动惯量，θl表示负载转角，tm表示电机电磁转矩，ωm表示电机角速度，tl表示负载转矩，ωl表示负载角速度，ks为传动系统扭转刚度，ts表示轴矩。

优选地，所述机械臂柔性关节电机端的转动惯量的方程表达式为：

式中，q为关节广义位移，τi为关节i的广义力；

mij为关节i和关节j之间的耦合量系数；

dijk为关节之间的向心力项、哥氏力项系数；

gi为关节i处重力项系数；

m(q)是n×n的正定对称矩阵，称为操作臂的惯性矩阵；是n×1的离心力和哥氏力向量；g(q)是n×1的重力矢量。

优选地，其中，mij的表达式为：

式中tp表示机器人的连杆变换矩阵。

优选地，变参数pi控制策略具有以下关系式成立：

kp＝jm(2ξa1ωa1+2ξb1ωb1)

式中：kp、ki分别为pi调节器比例参数、积分参数，ωa1、ωb1表示极点的自然频率；ξa1、ξb1表示极点阻尼系数。

优选地，采用相同幅值的极点配置法时，机械臂的柔性关节伺服系统动力学模型的闭环传递函数的零点如下式：

ξa1、ξb1取值决定了系统的最大超调量、峰值时间、调整时间；

kp、ki分别为pi调节器比例参数，z1、z2、z3表示零点的取值，ωa表示极点自然频率，j表示虚部，ξa1表示极点配置的阻尼系数。

优选地，采用相同阻尼系数的极点配置法时，机械臂的柔性关节伺服系统动力学模型的闭环传递函数的零点如下式：

ξ1、ωb1/ωa1取值决定了系统的最大超调量、峰值时间、调整时间；

kp、ki分别为pi调节器比例参数，z1、z2、z3表示零点的取值，ωa表示极点自然频率，j表示虚部，ξa1表示极点配置的阻尼系数，r表示阻尼比。

优选地，采用相同实部的极点配置法时，机械臂的柔性关节伺服系统动力学模型的闭环传递函数的零点如下式：

ξa1、ωb1/ωa1取值决定了系统的最大超调量、峰值时间、调整时间；

kp、ki分别为pi调节器比例参数，z1、z2、z3表示零点的取值，ωa表示极点自然频率，j表示虚部，ξa1表示极点配置的阻尼系数，r表示阻尼比，a、b表示分子分母。

(三)有益效果

本发明的有益效果是：本发明提供的一种基于pi控制策略的机械臂柔性关节位姿变换抑振方法具有以下有益效果：

在应用极点配置法时，首先考虑相同幅值、相同阻尼系数的极点配置方法。此两种方法可以适应惯量比变化较大的情况，并且对于阻尼系数的选取不是十分严格。若选择相同实部的极点配置方法，应谨慎选择阻尼系数，阻尼系数过大、过小都不能使系统达到稳定状态。

对于机器人柔性关节，其电机端、负载端的转动惯量与机器人的姿态、轨迹有关，在设计pi调节器参数时考虑惯量比的变化。通过仿真结果验证了本发明中基于极点配置的参数整定方法的有效性。

附图说明

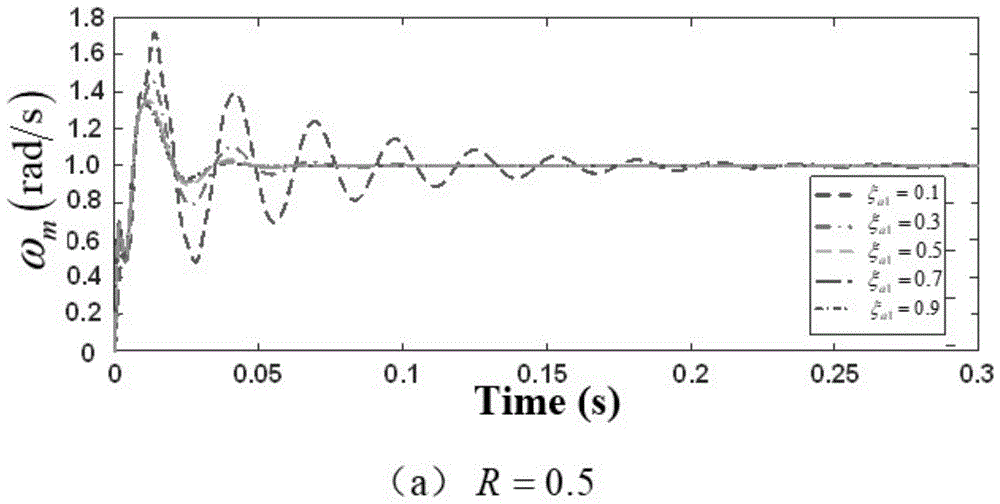
图1为本发明提供的一种基于pi控制策略的机械臂柔性关节位姿变换抑振方法中械臂相同幅值的极点配置策略仿真结果图a；

图2为本发明提供的一种基于pi控制策略的机械臂柔性关节位姿变换抑振方法中械臂相同幅值的极点配置策略仿真结果图b；

图3为本发明提供的一种基于pi控制策略的机械臂柔性关节位姿变换抑振方法中械臂相同幅值的极点配置策略仿真结果图c；

图4为本发明提供的一种基于pi控制策略的机械臂柔性关节位姿变换抑振方法中机械臂相同阻尼系数的极点配置法仿真结果图a；

图5为本发明提供的一种基于pi控制策略的机械臂柔性关节位姿变换抑振方法中机械臂相同阻尼系数的极点配置法仿真结果图b；

图6为本发明提供的一种基于pi控制策略的机械臂柔性关节位姿变换抑振方法中械臂相同幅值的极点配置策略仿真结果图c；

图7为本发明提供的一种基于pi控制策略的机械臂柔性关节位姿变换抑振方法中机械臂相同实部的极点配置法仿真结果图a；

图8为本发明提供的一种基于pi控制策略的机械臂柔性关节位姿变换抑振方法中机械臂相同实部的极点配置法仿真结果图b；

图9为本发明提供的一种基于pi控制策略的机械臂柔性关节位姿变换抑振方法机械臂相同实部的极点配置法仿真结果图c；

图10为本发明提供的一种基于pi控制策略的机械臂柔性关节位姿变换抑振方法的控制框图。

具体实施方式

为了更好的解释本发明，以便于理解，下面结合附图，通过具体实施方式，对本发明作详细描述。

如图10所示：本实施例公开了一种基于pi控制策略的机械臂柔性关节位姿变换抑振方法，建立机械臂的柔性关节伺服系统动力学模型，将变参数pi控制策略应用于机械臂的柔性关节伺服系统动力学模型的速度控制中；

其中，变参数pi控制策略的参数根据机械臂柔性关节电机端、负载端的转动惯量随位姿变化来进行调整；

其中，机械臂的柔性关节伺服系统动力学模型的方程表达式为：

式中：jm表示电机转动惯量，θm表示电机转角，jl表示负载转动惯量，θl表示负载转角，tm表示电机电磁转矩，ωm表示电机角速度，tl表示负载转矩，ωl表示负载角速度，ks为传动系统扭转刚度，ts表示轴矩。

本实施例中所述机械臂柔性关节电机端的转动惯量的方程表达式为：

式中，q为关节广义位移，τi为关节i的广义力；

mij为关节i和关节j之间的耦合量系数；

dijk为关节之间的向心力项、哥氏力项系数；

gi为关节i处重力项系数；

m(q)是n×n的正定对称矩阵，称为操作臂的惯性矩阵；是n×1的离心力和哥氏力向量；g(q)是n×1的重力矢量。

其中，mij的表达式为：

式中tp表示机器人的连杆变换矩阵。

本系统采用pi调节器时系统的闭环传递函数如下式所示。

式中kp、ki分别为pi调节器比例参数、积分参数。

应说明的是：本实施例中的变参数pi控制策略具有以下关系式成立：

kp＝jm(2ξa1ωa1+2ξb1ωb1)

kp、ki分别为pi调节器比例参数，ωa1、ωb1表示极点自然频率，jm表示电机端转动惯量，ωa表示反谐振频率、ξa1表示极点配置的阻尼系数。

本实施例中采用相同幅值的极点配置法时，机械臂的柔性关节伺服系统动力学模型的闭环传递函数的零点如下式：

ξa1、ξb1取值决定了系统的最大超调量、峰值时间、调整时间；

kp、ki分别为pi调节器比例参数，z1、z2、z3表示零点的取值，ωa表示极点自然频率，j表示虚部，ξa1表示极点配置的阻尼系数。

本实施例中采用相同阻尼系数的极点配置法时，机械臂的柔性关节伺服系统动力学模型的闭环传递函数的零点如下式：

ξ1、ωb1/ωa1取值决定了系统的最大超调量、峰值时间、调整时间；

kp、ki分别为pi调节器比例参数，z1、z2、z3表示零点的取值，ωa表示极点自然频率，j表示虚部，ξ1表示极点配置的阻尼系数。

本实施例中采用相同实部的极点配置法时，机械臂的柔性关节伺服系统动力学模型的闭环传递函数的零点如下式：

ξa1、ωb1/ωa1取值决定了系统的最大超调量、峰值时间、调整时间；

kp、ki分别为pi调节器比例参数，z1、z2、z3表示零点的取值，ωa表示极点自然频率，j表示虚部，ξa1表示极点配置的阻尼系数，r表示阻尼比，a、b表示分子分母。

为探究不同惯量比对系统谐振程度的影响，分别选择机械臂处于三种不r＝3.7三个特殊值。分别应用三种极点配置法进行数值仿真。仿真结果如图1-图9所示。由图1-图3可知：相同幅值的极点配置策略下，在ξa1∈(0,1)的区间上，随着阻尼系数的增大，系统超调量增大，动态响应特性变差，机械谐振程度增强。在ξa1∈(1,3)的区间上，随着阻尼系数的增大，系统超调量减小，机械谐振程度减弱。当阻尼系数ξa1为0.7时，阻尼系数对系统的影响不大。如图1所示：惯量比的取值选择过小时，电机速度到达理想转速后会出现一定程度的波动，不利于柔性关节伺服系统的控制。随着惯量比的增大，欠阻尼性逐渐减弱。该种方法相比较于另两种方法，系统调整时间较短。由图4-图6可知：在相同阻尼系数的极点配置策略下，在ξa1∈(0,1)的区间上，随着阻尼系数的增大，系统超调量减小，机械谐振程度减弱。当阻尼系数ξa1取值较小时电机转速达到理想后会出现一定的波动，不利于柔性关节伺服系统控制。当阻尼系数ξa1为0.7时，阻尼系数对系统的影响不大。对比图4-图6可知：随着惯量比的增大，电机达到理想转速后速度的波动程度减弱，欠阻尼性逐渐增强，此种现象在阻尼系数ξa1取小值时尤为明显。柔性关节伺服系统惯量比的增大使机械谐振程度加强，调整时间增加。该种方法相比较于另两种方法，系统超调量较大。

由图7-图9可知：在相同实部的极点配置策略下，在ξa1∈(0,1)的区间上，随着阻尼系数的增大，系统超调量增大，机械谐振程度增强。当阻尼系数ξa1为0.5时，阻尼系数对系统的影响不大。当阻尼系数较小时，柔性关节伺服系统不能达到稳定，随着惯量比的增大，这种现象愈加明显。对比图7、图8、图9可知：当ξa1取0.1时，随着柔性关节伺服系统惯量比的逐渐增大，系统逐步趋于不可控状态。由此可见惯量比对于系统的影响。应用该种方法选择ξa1取值过小所得系统不稳定。说明该种方法相比较于另两种方法，对于阻尼系数的选择有很大的局限性。

通过puma560机器人实例可以发现，电机端和负载端的转动惯量随机器人的位置、姿态变化而发生改变，由此导致双惯量系统的惯量比发生改变。此种惯量比的动态变化在机器人关节传动中较为常见。通过对比可以发现，相同的极点配置方法、相同的阻尼系数，因惯量比发生改变而导致系统控制失效。由此可见，在设计pi参数时应充分考虑惯量比变化的影响。通过上述实例可知，应用相同幅值和同阻尼系数的极点配置方法适合惯量比变化较大的情况。

以上结合具体实施例描述了本发明的技术原理，这些描述只是为了解释本发明的原理，不能以任何方式解释为对本发明保护范围的限制。基于此处解释，本领域的技术人员不需要付出创造性的劳动即可联想到本发明的其它具体实施方式，这些方式都将落入本发明的保护范围之内。