一种考虑变刚度关节延迟特性的机械臂控制变换方法与流程

1.本发明属于机械臂控制领域，涉及一种考虑变刚度关节的大延迟特性的机 械臂控制变换方法。


背景技术：

2.在非结构化环境下，变刚度关节在工业机器人或家用机器人上的应用会越 来越广泛，来解决环境交互完全性问题，之前一些采用变刚度关节的机器人或 者直接忽略变刚度延迟特性，无法保证实际系统的闭环稳定性；或者将复杂的 变刚度动力学和机器人动力学耦合设计控制，不但极大增加了控制器设计难度， 也限制了现有控制方法的直接推广应用。
3.从机械臂控制输入上说，除了机械臂的关节控制外，还额外加入了刚度量 作为输入，刚度量的在线调整使机器人的应用更加灵活。由于机器人的动力学 本身就非常复杂，在把刚度作为控制量时，如果把变刚度的动态特性考虑在内， 会大大增加控制器设计难度，一般忽略其动态特性直接设计。但实际上，变刚 度关节一般采用物理方法改变弹簧的压紧或者改变力臂的大小进行刚度调整， 刚度变化的响应速度延迟较大，这会给控制的稳定性带来比较大的影响。


技术实现要素：

4.本发明解决的技术问题是：克服现有技术的不足，提供一种考虑变刚度关 节延迟特性的机械臂控制变换方法。
5.本发明解决技术的方案是：一种考虑变刚度关节延迟特性的机械臂控制变 换方法，通过下述方式实现：
6.(1)考虑机械臂安装变刚度关节的时延特性，建立n自由度机械臂动力学 模型；
7.(2)将所述动力学模型中的时延缩小为原来的建立新的动力学模型； 所述的m＞1；
8.(3)设计使新动力学模型闭环稳定的小时延控制律；
9.(4)以所述的小时延控制律为基础，考虑步骤(1)、(2)中两个动力学 模型的缩放关系，进行缩放变换，设计使步骤(1)闭环稳定的控制律，利用该 控制律实现机械臂的控制。
10.优选的，在步骤(2)之前首先分析机械臂的时延特性，若时延大于机械臂 控制周期，则从步骤(2)开始执行；否则，直接设计使步骤(1)动力学模型 闭环稳定的小时延控制律，利用该控制律对机械臂进行控制。
11.优选的，假设步骤(3)设计的小时延控制律为：
[0012][0013]
[0014]
则步骤(4)中设计的控制律为：
[0015][0016][0017]
式中，u为n维力矩向量，对应n自由度机械臂的关节力矩，k为l维刚度向 量，对应n自由度机械臂l个刚度可调关节的刚度输入，u0()和k0()分别指现有 的力矩和刚度的控制函数，q和对应n自由度机械臂的关节角度向量和关节角 速度向量，g(q)是拉格朗日方程中的重力梯度向量，δq为l个刚度可调关节的 形变角度；t为时间，b为n
×
n矩阵描述了关节力矩对广义坐标的作用效果。
[0018]
优选的，所述步骤(1)中的动力学模型如下：
[0019][0020]
式中，q为结构空间的一个广义坐标向量，维数为n；d(q)为惯性矩阵； 是科里奥利矩阵，g(q)是重力势能场的梯度向量，b为n
×
n矩阵描述了关 节力矩对广义坐标的作用效果，e(δq)为n
×
l矩阵，将刚度可变关节的关节形变 作用映射到广义坐标上，l为刚度可调关节数，满足l≤n，假设n自由度机械臂 第i个关节刚度不可调，则e(δq)第i行为全零行，假设n自由度机械臂第i个关 节刚度可调，且对应的是l个刚度可调关节中的第j个，则e(δq)第i行j列的元 素为δq
j
，第i行其余元素为0；u(t)代表n维力矩向量，k(t)为l个刚度可调关节 的刚度输入，t＝[t1,t2,
…
t
l
]
t
分别对应l个可调节刚度关节的刚度调节时延，有 k(t-t)＝[k1(t-t1) k2(t-t2)
ꢀ…ꢀ
k
l
(t-t
l
)]
t
。
[0021]
优选的，所述步骤(2)中的新动力学模型如下：
[0022][0023]
优选的，所述的m根据实际的时延t＝[t1,t2,
…
t
l
]
t
选取，一般需要保证建立 的新的动力学模型的时延小于机械臂上位机规划控制器一个控制周期的时长 δt，其中l为机械臂中可调节刚度关节的数量。
[0024]
m取值范围优选其中，t
max
是时延t＝[t1,t2,
…
t
l
]
t
中的最大分 量。
[0025]
本发明与现有技术相比的有益效果是：
[0026]
机械臂采用的变刚度关节，一般用物理方法改变弹簧的张紧力或者改变支 撑点力臂的大小进行刚度调整，刚度变化的响应速度延迟较大，如果把变刚度 的动态特性考虑在内，会大大增加控制器设计难度，现有的控制律设计一般忽 略其动态特性直接设计。但实际应用中，较大的延迟有可能使系统不稳定。为 了在机械臂进行相关操作时保证稳定性和操作精度，本申请给出了一种时间放 缩方法，将变刚度关节的动态特性考虑在内，能够将忽略动态特性直接设计出 的控制律通过相应的控制变换，转化成实用的控制，通过牺牲一定的动态性能， 来确保带有变刚度关节的机械臂操作过程的稳定性和稳态精度。
[0027]
本发明提出了一种考虑变刚度调节延迟的控制变换方法，能够将一些现有 的控
制律直接推广应用到考虑变刚度大延迟特性的情况下，可确保机械臂操作 过程的稳定性和稳态精度。
附图说明
[0028]
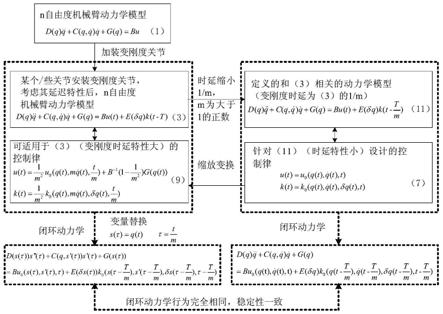
图1为本发明流程图。
具体实施方式
[0029]
下面结合实施例对本发明作进一步阐述。
[0030]
本发明的基本原理为：采用时间放缩的方法，将变刚度关节的动态特性考 虑进机械臂的控制设计中，在牺牲一定的响应速度的条件下，可以保证系统的 稳定性和稳态精度。
[0031]
如图1所示，一种考虑变刚度关节延迟特性的机械臂控制变换方法，通过 下述方式实现：
[0032]
(1)考虑机械臂安装变刚度关节的时延特性，建立n自由度机械臂动力学 模型；
[0033]
(2)将所述动力学模型中的时延缩小为原来的建立新的动力学模型； 所述的m＞1；
[0034]
(3)设计使新动力学模型闭环稳定的小时延控制律：
[0035][0036]
(4)以所述的小时延控制律为基础，考虑步骤(1)、(2)中两个动力学 模型的缩放关系，进行缩放变换，设计使步骤(1)闭环稳定的控制律：
[0037]
利用该控制律实现机械臂的控制。
[0038]
方案验证
[0039]
考虑一个n自由度机械臂的通用模型，设q为结构空间的一个广义坐标向 量，维数为n，u为一个n维的力矩向量，机器人的数学模型可以描述为一个受 控的拉格朗日系统
[0040][0041]
其中，d(q)是系统的惯性矩阵。是科里奥利矩阵，是重力 势能场的梯度向量，v(q)是系统重力势能，b为n
×
n矩阵描述了关节力矩对广 义坐标的作用效果，u为输入的n维力矩向量。
[0042]
当机械臂某个关节或者某些关节安装了变刚度关节时，动力学变为
[0043][0044]
k为l个刚度可调关节的刚度输入，e(δq)为n
×
l矩阵，将刚度可变关节的关 节形
变作用映射到广义坐标上，l为刚度可调关节数，满足l≤n，假设n自由度 机械臂第i个关节刚度不可调，则e(δq)第i行为全零行，假设n自由度机械臂第 i个关节刚度可调，且对应的是l个刚度可调关节中的第j个，则e(δq)第i行j列 的元素为δq
j
，第i行其余元素为0。
[0045]
则可以把u和k均当作系统输入来调节机械臂的运动。实际上，机械臂的关 节刚度k＝[k
1 k2ꢀ…ꢀ
k
l
]
t
的改变，是通过变刚度电机通过角位置的调节取得的， 刚度响应速度和输入u的响应速度相比有个比较大的延迟，并且这个延迟和关 节位置，形变元件的形变量，变刚度电机的动态响应速度都有关系，建模是相 当复杂的，设机械臂上位机规划控制器一个控制周期的时长δt，变刚度关节时 间延迟的值要大于δt，设向量t＝[t1,t2,
…
t
l
]
t
分别对应l个可调节刚度关节的刚 度调节时延，则系统动力学模型可以写成(下称系统(3))
[0046][0047]
其中，k(t-t)＝[k1(t-t1) k2(t-t2)
ꢀ…ꢀ
k
l
(t-t
l
)]
t
。
[0048]
现在引入一个新的变量其中m>1，定义变量
[0049]
s(τ)＝q(t)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(4)
[0050]
设
[0051][0052]
则可得到
[0053][0054]
当忽略系统(3)时延时，考虑如下的控制律，
[0055][0056]
注意到u0和k0为系统状态以及时间的函数，此表达式具有一般性，可以代 表在忽略关节延迟特性情况下，采用现有理论方法设计出来的任一种状态反馈 或者输出反馈控制律。
[0057]
把新变量(4)、(5)和(6)代入方程(3)
[0058][0059]
如果把(7)换成如下的控制律
[0060][0061]
代入公式(3)经过新变量变换后，则变为
[0062][0063]
定义一个相关系统(下称系统(11))
[0064][0065]
可以看出其变刚度动态时延较小，为原系统(3)时延的
[0066]
如果把最初定义的控制律(7)代入，可以得到系统闭环为
[0067][0068]
观察可得，方程(10)和(12)除了变量s和τ分别被q和t替换，其动力 学的演化行为完全相同，也就是说，如果系统变刚度动态时延很小的系统(11) 在控制律(7)的作用下闭环稳定，则动力学方程(10)闭环稳定。注意到系 统变刚度动态时延很大的系统(3)在控制律(9)下的闭环行为等价于方程(10)， 这是通过应用时间放缩变换得到的。可以得到结论，如果控制律(7)稳定系统 (11)，则控制律(9)稳定系统(3)。由此，对于变刚度动态时延较大的系统 (3)的控制问题，应用本申请提出的方法可以转换成对变刚度动态时延很小的 系统(11)的控制问题。
[0069]
对于机械臂关节跟踪问题来说，如果小时延系统(11)在控制律(7)的作 用下能渐近稳定跟踪参考输出q
d
(mt)，则大时延系统(3)在控制律(9)作用 下能跟踪参考输出q
d
(t)，在这种放缩变换中，m的值可以根据实际的时延 t＝[t1,t2,
…
t
l
]
t
酌情选取，设t
max
是时延t＝[t1,t2,
…
t
l
]
t
中的最大分量，根据经验， 选取时，一般可通过整定其他控制参数使系统稳定，但系统鲁棒性有限； 选取时，可比较容易确保系统稳定，且鲁棒性较好，当m的值选取过大 时，会使系统的动态响应过慢。一般情况下，选取这样针对系 统(11)的控制器(7)的设计将会变得非常容易，现有的控制律大部分都是按 照此假设条件设计，应用本发明给出的变换关系，根据控制律(7)可变换得到 控制律(9)，控制律(9)即可适用于变刚度时延特性较大的实际系统(3)。
[0070]
本发明提出了一种基于时间放缩变换的方法，能够将忽略动态特性直接设 计出来的控制律通过相应的控制变换，转化成实用的、将变刚度的较大时延特 性考虑在内的控制，通过牺牲一定的动态性能，来确保机械臂操作过程的稳定 性和稳态精度。
[0071]
本发明提出的控制变换方法，可以用于各种采用了变刚度关节的机械臂控 制中，此方法结果明确，具有一般性，可以弥补现有控制律设计中针对变刚度 延迟特性存在的问题。本发明适用范围广，实用性强，可以比较广泛地应用于 非结构化环境下，带有变刚度关节的工业机器人或家用机器人的运动控制，具 有较好的应用前景。
[0072]
本发明未详细说明部分属于本领域技术人员的公知常识。