基于有限时间输出状态受限的多关节机械臂阻抗控制方法与流程

[0001]
本发明属于机器人控制技术领域，尤其涉及一种基于有限时间输出状态受限的多关节机械臂阻抗控制方法。


背景技术：

[0002]
近年来，多关节机械臂技术的应用愈发普及，其结构越发繁杂化、精密化。因此，为确保该技术的安全性和合规性，迫切需要更高精度的力/位控制方法。在这一领域，众多学者做了大量研究工作，并给出大量控制方法，例如力/位混合控制方法、阻抗控制方法等。
[0003]
其中，阻抗控制作为解决力/位控制问题的重要方法，该方法具有抗扰动能力强、计算量相对较少以及易于机械臂进行力控制等优点，受到广泛关注。
[0004]
应用于多关节机械臂的基于反步法设计的阻抗控制方法发展迅速，已经被运用到多机械臂系统的控制中，并取得了较好的力/位控制效果，但仍然存在不足之处，主要体现在：
[0005]
(1)多关节机械臂是一个复杂的非线性系统；(2)机械臂的输出力/位存在各种约束条件的限制，超出机械臂约束条件限制的范围，会降低机械臂工作性能，影响产品质量，同时不仅会缩短其使用寿命，极易造成机械臂硬件损伤，甚至可能引发灾难性后果，威胁操作人员的人身安全。上述问题的存在使得反步法的使用具有较大的局限性。
[0006]
针对上述技术问题(1)，模糊逻辑系统对系统的某些函数必须是线性的问题提供了解决思路，其中，模糊逻辑系统通过近似理论逼近复杂非线性系统中的非线性函数，提高抗干扰性能和鲁棒性。而针对上述技术问题(2)，即目前控制器设计中存在的输出状态可能超出许可范围的问题，还没有很好的解决思路，因而，无法保证系统的安全运行。


技术实现要素：

[0007]
本发明提出了一种基于有限时间输出状态受限的多关节机械臂阻抗控制方法，通过对输出信号进行约束，在保证机械臂输出力/位状态被约束在有界区间中的前提下，确保系统的安全运行。本发明为了实现上述目的，采用如下技术方案：
[0008]
基于有限时间输出状态受限的多关节机械臂阻抗控制方法，包括如下步骤：
[0009]
a.建立多关节机械臂的动力学模型，如公式(1)所示：
[0010][0011]
其中，q∈r
n
×1为多关节机械臂各关节角度，分别表示多关节机械臂各关节角度变化速度和加速度；d(q)为多关节机械臂惯性矩阵；为多关节机械臂离心力和科里奥利力矩阵；g(q)为多关节机械臂重力项向量；τ∈r
n
×1为真实控制律；τ
f
∈r
n
×1为多关节机械臂各关节所受的摩擦力向量；τ
d
∈r
n
×1是多关节机械臂各关节所受的外部干扰项向量；j(q)∈r
n
×
n
为多关节机械臂的雅可比矩阵；f
e
∈r
n
×1为环境对多关节机械臂末端施加的接触力；r
n
×1为n维实数集，r
n
×
n
为n
×
n维实数集，n为多关节机械臂的关节数；
[0012]
多关节机械臂在笛卡尔坐标系上的关系式，如公式(2)所示：
[0013][0014]
其中，x为多关节机械臂末端位置，为多关节机械臂关节角度转化为笛卡尔坐标下机械臂末端位置的函数关系式；整理得到下面公式：
[0015][0016]
多关节机械臂末端位置与末端力的阻抗控制关系式，如公式(3)所示：
[0017][0018]
其中，e＝x-x
d
，f
d
为多关节机械臂末端期待力，m
d
为多关节机械臂期待惯性矩阵，b
d
为多关节机械臂期待阻尼矩阵，k
d
为多关节机械臂刚性矩阵；
[0019]
x
d
＝[x
d1
,x
d2
,
…
,x
dn
]
t
为多关节机械臂末端期待轨迹，x
d1
,x
d2
,
…
,x
dn
表示x
d
的分量；
[0020]
将公式(2)代入公式(1)，得到：
[0021][0022]
其中，
[0023]
设x1＝x，则由公式(4)写出公式(5)：
[0024][0025]
其中，x1表示多关节机械臂末端位置，x1＝[x
11
,x
12
,
…
,x
1n
]
t
；x2表示多关节机械臂末端运动速度，x2＝[x
21
,x
22
,
…
,x
2n
]
t
；
[0026]
b.根据有限时间输出状态受限技术和自适应反步法原理，设计真实控制律τ使得多关节机械臂末端位置x1跟踪多关节机械臂末端期待轨迹x
d
；
[0027]
假设f(z)在紧集ω
z
中是一个连续的函数，对于任意的常数ε＞0，总存在一个模糊逻辑函数w
t
s(z)满足：其中，输入向量q是模糊输入维数，r
q
为实数向量集；w∈r
o
是模糊权向量，模糊节点数o为正整数，且o＞1，r
o
为实数向量集；
[0028]
s(z)＝[s1(z),...,s
o
(z)]
t
∈r
o
为基函数向量，s1(z),...,s
o
(z)分别为s(z)的基函数；选取基函数s
j
(z)为如下的高斯函数：其中，μ
j
＝[μ
j1
,μ
j2
,
…
,μ
jr
]是高斯函数分布曲线的中心位置，而η
j
则为高斯函数的宽度；μ
j1
,μ
j2
,
…
,μ
jr
为μ
j
的基向量；
[0029]
定义有限时间稳定：
[0030]
考虑非线性系统对于光滑正定函数v(ξ)，存在a＞0、b＞0和0＜γ＜1，使得成立，则非线性系统是半全局有限时间稳定；
[0031]
收敛时间t
s
通过公式：
[0032]
t
s
＝1/(va-γva)[v
1-γ
(ξ(0))-(b/(a-va))
(1-γ)/γ
]来估计，且
[0033]
其中，0＜v＜1，ξ(0)表示非线性系统的初始值；
[0034]
对于任何向量k∈r
n
，以下不等式对于满足|l|＜|k|的任意向量l∈r
n
均成立：
[0035][0036]
定义虚拟控制律α1＝[α
11
,α
12
,
…
,α
1n
]
t
；
[0037]
定义误差变量
[0038]
其中，z
1i
＝x
1i-x
di
表示i方向多关节机械臂末端位置与期待轨迹之间的误差，z
2i
＝x
2i-α
1i
表示i方向多关节机械臂末端运动速度和虚拟控制律之间的误差，i＝1,2,
…
,n；
[0039]
定义如下两个紧集：
[0040]
ω
a
＝{|z
1i
|＜k
ai
}，k
ai
为正常数；ω
c
＝{|x
1i
|＜k
ci
}，k
ci
为正常数，i＝1,2,
…
,n；
[0041]
误差变量z
1i
受限区间的界k
ai
＝k
c1i-x
di
，x
di
＝max{|x
di
|}；
[0042]
其中，k
c1i
为多关节机械臂末端位置x
1i
设定的受限区间的界，设k
a
＝[k
a1
,k
a2
,
…
,k
an
]
t
；
[0043]
基于有限时间输出状态受限的多关节机械臂阻抗控制方法设计选取一个障碍lyapunov函数来构建真实控制律，当误差变量趋向于受限区间的界时，障碍lyapunov函数值将趋向于无穷大，进而保证误差变量始终保持在受限区间内；具体包括如下步骤：
[0044]
b.1.对于多关节机械臂末端期待轨迹x
d
，选取障碍lyapunov函数
[0045]
对v1求导得到：
[0046][0047]
选取虚拟控制律α1＝[α
11
,α
12
,
…
,α
1n
]
t
，其中：
[0048][0049]
式中，k
1i
为正常数，i＝1,2,...,n；定义k1＝[k
11
,k
12
,
…
,k
1n
]
t
；
[0050]
虚拟控制律
[0051]
其中，
[0052]
将公式(8)和公式(9)代入公式(7)，得到：
[0053]
[0054]
由杨氏不等式得到：
[0055]
将式(11)代入式(10)，得到：
[0056]
b.2.选取lyapunov函数对v2求导得到：
[0057][0058]
误差变量z2对时间求导得到：
[0059][0060]
设f(z)＝-δ-1
(q)(τ
f
+τ
d
)，定义非线性函数f(z)＝[f1(z),
…
,f
n
(z)]
t
，根据万能逼近定理，对于任意小的常数ε
i
＞0，存在模糊逻辑函数w
it
s(z)使得f
i
(z)＝w
it
s(z)+δ
i
；
[0061]
其中，δ
i
表示逼近误差，并满足δ
i
≤ε
i
，i＝1,
…
,n；
[0062]
由于z2＝[z
21
,z
22
,
…
,z
2n
]
t
，由杨氏不等式得到：
[0063][0064]
其中，l是一个大于零的常数，w
i
表示模糊权向量，||w
i
||表示w
i
的范数；
[0065]
定义θ＝max{||w1||2,||w2||2,
…
,||w
n
||2}，公式(15)写成：
[0066][0067]
定义则：
[0068][0069]
选取真实控制律τ如下：
[0070][0071]
其中，k2表示大于零的常数，表示θ的估计值；
[0072]
将公式(16)、(17)和(18)代入公式(13)，定义估计误差为得到：
[0073][0074]
b.3.选择lyapunov函数：其中，r为大于零的常数，对v求导得到：
[0075][0076]
选取自适应律：
[0077]
其中，m为大于零的常数；
[0078]
c.对构建的基于有限时间输出状态受限的多关节机械臂阻抗控制方法进行稳定性分析；
[0079]
将公式(21)代入公式(20)，得到公式(22)：
[0080][0081]
由杨氏不等式得到：
[0082]
将式(23)代入式(22)，得：
[0083][0084]
当得：
[0085][0086]
当得：
[0087][0088]
由式(25)、(26)得式(27)：
[0089][0090]
当满足条件|z
1i
|≤k
ai
，0＜γ＜1时，下列不等式成立：
[0091][0092]
将公式(27)及(28)代入式(24)，得到：
[0093][0094]
其中，a＝min{min{2
γ
k
1i
},2
γ
k2,m
γ
}，
[0095]
由公式(29)得知，当选择参数满足k
1i
＞0，k2＞0以及m＞0时，保证a＞0以及b＞0；
[0096]
根据有限时间稳定的定义，确定t
s
，如公式(30)所示：
[0097][0098]
其中，0＜v＜1，v
1-γ
(0)表示选取lyapunov函数v的初始值的1-γ次方；
[0099]
对于满足
[0100]
以上不等式表明闭环系统中的误差信号是半全局有限时间稳定的；进一步得知，初始条件满足z1(0)∈ω0＝{z1∈r
n
:|z1|＜|k
a
|}时，得到|z
1i
|＜|k
ai
|，i＝1,2,
…
n，由公式x1＝z1+x
d
以及公式|x
di
(t)|≤x
di
，i＝1,2,
…
,n，得出|x
1i
|＜k
ai
+x
di
＝k
c1i
，i＝1,2,
…
,n，
[0101]
因此，机械臂输出力/位状态被约束在设定有界区间之中。
[0102]
本发明具有如下优点：
[0103]
如上所述，本发明述及了一种基于有限时间输出状态受限的多关节机械臂阻抗控制方法，该方法利用有限时间技术与阻抗控制技术相结合，实现了在有限时间内使多关节机械臂末端较好地进行力/位跟踪，并减少了机械臂力/位跟踪误差；利用模糊逻辑系统逼近多关节机械臂系统中的未知非线性函数，有效地处理了机械臂系统中的未知非线性项，使机械臂在摩擦力函数不确定情况下实现较好的力/位跟踪控制；此外，本发明通过引入障碍lyapunov函数的运用对系统输出信号进行约束，以保证机械臂输出力/位状态可以被约束在有界区间内，从而保证了系统运行的安全。本发明控制方法具有更强的鲁棒性，更加符合实际工程运用。
附图说明
[0104]
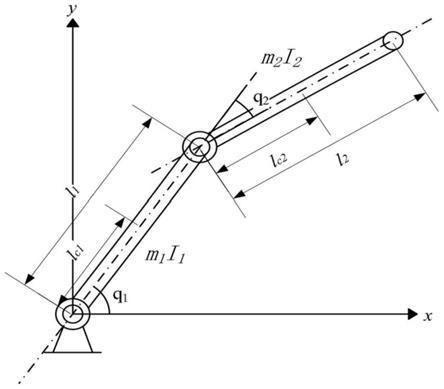
图1为本发明实施例中采用二自由度机械臂的模型示意图；
[0105]
图2为采用本发明控制方法后机械臂末端x轴方向跟踪曲线仿真图；
[0106]
图3为采用本发明控制方法后机械臂末端x轴方向跟踪误差仿真图；
[0107]
图4为采用本发明控制方法后机械臂末端y轴方向跟踪曲线仿真图；
[0108]
图5为采用本发明控制方法后机械臂末端y轴方向跟踪误差仿真图；
[0109]
图6为采用本发明控制方法后机械臂末端x轴方向力跟踪仿真图；
[0110]
图7为采用本发明控制方法后机械臂末端x轴方向力跟踪误差仿真图；
[0111]
图8为采用本发明控制方法后机械臂末端y轴方向力跟踪仿真图；
[0112]
图9为采用本发明控制方法后机械臂末端y轴方向力跟踪误差仿真图；
[0113]
图10为采用本发明控制方法后二关节机械臂各关节力矩仿真图。
具体实施方式
[0114]
本发明的基本思想为：
[0115]
基于阻抗控制技术，运用反步法构造中间虚拟控制信号，逐步递推得到控制律，从而对多关节机器臂的末端执行器进行控制；利用模糊自适应技术逼近多关节机械臂系统中的未知摩擦量和外部扰动量，提高系统抗干扰性能与鲁棒性，引入障碍lyapunov方程对机械臂的输出控制信号进行约束，使其输出力/位状态处于有限区间范围之内以确保系统运行安全，利用有限时间控制使机械臂力/位跟踪信号在有限时间内收敛，保证了机械臂力/位跟踪误差能在有限时间内收敛到原点的一个足够小的领域内。以上发明构思保证本发明方法能够使机械臂末端力/位能快速准确地跟踪期望轨迹，并且使其控制误差在一个合理的范围内。
[0116]
下面结合附图以及具体实施方式对本发明作进一步详细说明：
[0117]
基于有限时间输出状态受限的多关节机械臂阻抗控制方法，包括如下步骤：
[0118]
a.建立多关节机械臂的动力学模型，如公式(1)所示：
[0119][0120]
其中，q∈r
n
×1为多关节机械臂各关节角度，分别表示多关节机械臂各关节角度变化速度和加速度；d(q)为多关节机械臂惯性矩阵；为多关节机械臂离心力和科里奥利力矩阵；g(q)为多关节机械臂重力项向量；τ∈r
n
×1为真实控制律；τ
f
∈r
n
×1为多关节机械臂各关节所受的摩擦力向量；τ
d
∈r
n
×1是多关节机械臂各关节所受的外部干扰项向量；j(q)∈r
n
×
n
为多关节机械臂的雅可比矩阵；f
e
∈r
n
×1为环境对多关节机械臂末端施加的接触力；r
n
×1为n维实数集，r
n
×
n
为n
×
n维实数集，n为多关节机械臂的关节数。
[0121]
多关节机械臂在笛卡尔坐标系上的关系式，如公式(2)所示：
[0122][0123]
其中，x为多关节机械臂末端位置，为多关节机械臂关节角度转化为笛卡尔坐标下机械臂末端位置的函数关系式。整理得到下面公式：
[0124][0125]
多关节机械臂末端位置与末端力的阻抗控制关系式，如公式(3)所示：
[0126][0127]
其中，e＝x-x
d
，f
d
为多关节机械臂末端期待力，m
d
为多关节机械臂期待惯性矩阵，b
d
为多关节机械臂期待阻尼矩阵，k
d
为多关节机械臂刚性矩阵。
[0128]
x
d
＝[x
d1
,x
d2
,
…
,x
dn
]
t
为多关节机械臂末端期待轨迹，x
d1
,x
d2
,
…
,x
dn
表示x
d
的分量；
[0129]
将公式(2)代入公式(1)，得到：
[0130][0131]
其中，
[0132]
设x1＝x，则由公式(4)写出公式(5)：
[0133][0134]
其中，x1表示多关节机械臂末端位置，x1＝[x
11
,x
12
,
…
,x
1n
]
t
；x2表示多关节机械臂末端运动速度，x2＝[x
21
,x
22
,
…
,x
2n
]
t
。
[0135]
b.根据有限时间输出状态受限技术和自适应反步法原理，设计真实控制律τ使得多关节机械臂末端位置x1跟踪多关节机械臂末端期待轨迹x
d
。
[0136]
假设f(z)在紧集ω
z
中是一个连续的函数，对于任意的常数ε＞0，总存在一个模糊逻辑函数w
t
s(z)满足：其中，输入向量q是模糊输入维数，
r
q
为实数向量集；w∈r
o
是模糊权向量，模糊节点数o为正整数，且o＞1，r
o
为实数向量集。
[0137]
s(z)＝[s1(z),...,s
o
(z)]
t
∈r
o
为基函数向量，s1(z),...,s
o
(z)分别为s(z)的基函数；选取基函数s
j
(z)为如下的高斯函数：其中，μ
j
＝[μ
j1
,μ
j2
,
…
,μ
jr
]是高斯函数分布曲线的中心位置，而η
j
则为高斯函数的宽度；μ
j1
,μ
j2
,
…
,μ
jr
为μ
j
的基向量。
[0138]
定义有限时间稳定：
[0139]
考虑非线性系统对于光滑正定函数v(ξ)，存在a＞0、b＞0和0＜γ＜1，使得成立，则非线性系统是半全局有限时间稳定。
[0140]
收敛时间t
s
通过公式：
[0141]
t
s
＝1/(va-γva)[v
1-γ
(ξ(0))-(b/(a-va))
(1-γ)/γ
]来估计，且
[0142]
其中，0＜v＜1，ξ(0)表示非线性系统的初始值。
[0143]
对于任何向量k∈r
n
，以下不等式对于满足|l|＜|k|的任意向量l∈r
n
均成立：
[0144][0145]
定义虚拟控制律α1＝[α
11
,α
12
,
…
,α
1n
]
t
；
[0146]
定义误差变量
[0147]
其中，z
1i
＝x
1i-x
di
表示i方向多关节机械臂末端位置与期待轨迹之间的误差，z
2i
＝x
2i-α
1i
表示i方向多关节机械臂末端运动速度和虚拟控制律之间的误差，i＝1,2,
…
,n。
[0148]
定义如下两个紧集：
[0149]
ω
a
＝{|z
1i
|＜k
ai
}，k
ai
为正常数；ω
c
＝{|x
1i
|＜k
ci
}，k
ci
为正常数，i＝1,2,
…
,n；
[0150]
误差变量z
1i
受限区间的界k
ai
＝k
c1i-x
di
，x
di
＝max{|x
di
|}。
[0151]
其中，k
c1i
为多关节机械臂末端位置x
1i
设定的受限区间的界，设k
a
＝[k
a1
,k
a2
,
…
,k
an
]
t
。
[0152]
基于有限时间输出状态受限的多关节机械臂阻抗控制方法设计选取一个障碍lyapunov函数来构建真实控制律，当误差变量趋向于受限区间的界时，障碍lyapunov函数值将趋向于无穷大，进而保证误差变量始终保持在受限区间内。具体包括如下步骤：
[0153]
b.1.对于多关节机械臂末端期待轨迹x
d
，选取障碍lyapunov函数
[0154]
对v1求导得到：
[0155][0156]
选取虚拟控制律α1＝[α
11
,α
12
,
…
,α
1n
]
t
，其中：
[0157][0158]
式中，k
1i
为正常数，i＝1,2,
…
,n；定义k1＝[k
11
,k
12
,
…
,k
1n
]
t
。
[0159]
虚拟控制律
[0160]
其中，
[0161]
将公式(8)和公式(9)代入公式(7)，得到：
[0162][0163]
由杨氏不等式得到：
[0164]
将式(11)代入式(10)，得到：
[0165]
b.2.选取lyapunov函数对v2求导得到：
[0166][0167]
误差变量z2对时间求导得到：
[0168][0169]
设f(z)＝-δ-1
(q)(τ
f
+τ
d
)，定义非线性函数f(z)＝[f1(z),
…
,f
n
(z)]
t
，根据万能逼近定理，对于任意小的常数ε
i
＞0，存在模糊逻辑函数w
it
s(z)使得f
i
(z)＝w
it
s(z)+δ
i
。
[0170]
其中，δ
i
表示逼近误差，并满足δ
i
≤ε
i
，i＝1,
…
,n。
[0171]
由于z2＝[z
21
,z
22
,
…
,z
2n
]
t
，由杨氏不等式得到：
[0172][0173]
其中，l是一个大于零的常数，w
i
表示模糊权向量，||w
i
||表示w
i
的范数。
[0174]
定义θ＝max{||w1||2,||w2||2,
…
,||w
n
||2}，公式(15)写成：
[0175][0176]
定义则：
[0177][0178]
选取真实控制律τ如下：
[0179]
[0180]
其中，k2表示大于零的常数，表示θ的估计值。
[0181]
将公式(16)、(17)和(18)代入公式(13)，定义估计误差为得到：
[0182][0183]
b.3.选择lyapunov函数：其中，r为大于零的常数，对v求导得到：
[0184]
选取自适应律：
[0185]
其中，m为大于零的常数。
[0186]
c.对构建的基于有限时间输出状态受限的多关节机械臂阻抗控制方法进行稳定性分析。
[0187]
将公式(21)代入公式(20)，得到公式(22)：
[0188][0189]
由杨氏不等式得到：
[0190]
将式(23)代入式(22)，得：
[0191][0192]
当得：
[0193][0194]
当得：
[0195][0196]
由式(25)、(26)得式(27)：
[0197][0198]
当满足条件|z
1i
|≤k
ai
，0＜γ＜1时，下列不等式成立：
[0199][0200]
将公式(27)及(28)代入式(24)，得到：
[0201][0202]
其中，a＝min{min{2
γ
k
1i
},2
γ
k2,m
γ
}，
[0203]
由公式(29)得知，当选择参数满足k
1i
＞0，k2＞0以及m＞0时，保证a＞0以及b＞0。
[0204]
根据有限时间稳定的定义，确定t
s
，如公式(30)所示：
[0205][0206]
其中，0＜v＜1，v
1-γ
(0)表示选取lyapunov函数v的初始值的1-γ次方。
[0207]
对于满足
[0208]
以上不等式表明闭环系统中的误差信号是半全局有限时间稳定的；进一步得知，初始条件满足z1(0)∈ω0＝{z1∈r
n
:|z1|＜|k
a
}时，得到|z
1i
|＜|k
ai
|，i＝1,2,
…
n，
[0209]
由公式x1＝z1+x
d
以及公式|x
di
(t)|≤x
di
，i＝1,2,
…
,n，得出|x
1i
|＜k
ai
+x
di
＝k
c1i
，i＝1,2,
…
,n，因此，机械臂输出力/位状态被约束在设定有界区间之中。
[0210]
在虚拟环境下对所建立的基于有限时间输出状态受限的多关节机械臂阻抗控制方法进行仿真，以验证所提出控制方法的可行性。
[0211]
在垂直平面上的二自由度机械臂如图1所示，仿真实验将会证明所提出控制方法的有效性。仿真实验的旋转关节二自由度机械臂系统模型表示如下：
[0212][0213]
其中，
[0214]
在图1中，m
i
和l
i
分别为机械臂第i节连杆的质量和长度，l
ci
为机械臂第i-1个关节到i节连杆质心的距离，i
i
为关节i基于坐标轴穿过关节的质心的转动惯量。
[0215]
x1＝[x
11
,x
12
]
t
,其中，x
11
和x
12
分别表示二自由度机械臂在笛卡尔坐标系上机械臂末端在x、y轴上的位置x1和y1。
[0216]
x
d
＝[x
d1
,x
d2
]，其中，x
d1
和x
d2
分别表示机械臂期待轨迹在x、y轴上的位置x
1d
和y
1d
。
[0217]
q＝[q1,q2]
t
表示机械臂各关节角度。
[0218]
f
e
＝[f
e1
,f
e2
]
t
，其中，f
e1
和f
e2
分别表示二自由度机械臂在笛卡尔坐标系上机械臂末端在x、y轴方向的力矩f
x
和f
y
。
[0219]
f
d
＝[f
d1
,f
d2
]
t
,其中，f
d1
和f
d2
分别代表机械臂末端期待力在x、y轴方向的力矩f
xd
和f
yd
。
[0220]
二自由度机械臂的惯性矩阵d(q)、科里奥利力与离心力矩阵重力项矩阵g(q)定义如下所示：
[0221][0222][0223][0224]
二自由度机械臂的雅可比矩阵j(q)定义如下所示：
[0225][0226]
二自由度机械臂的参数关节1、2质量m1、m2均为1.00kg；关节1、2长度l1、l2均为1.00m；关节1、2转动惯量i1、i2均为0.25kgm2。
[0227]
机械臂初始参数为x
11
＝x
12
＝0.5，二自由度机械臂末端的期待跟踪轨迹如下所示x
d
＝[0.7+0.2cos(t),0.7+0.2sin(t)]
t
，其中，t∈[0,20]。
[0228]
对于二自由度机械臂的有限时间输出状态受限阻抗控制，控制参数选取k1＝[3,3]
t
，k2＝2，k
a
＝[0.6,0.6]
t
，γ＝0.8，l＝0.5，m＝0.25，n＝2。
[0229]
该二自由度机械臂期待阻抗选为m
d
＝i，b
d
＝diag[10,10]，k
d
＝diag[70,70]。
[0230]
模糊隶属度函数为：
[0231][0232][0233][0234]
其中，i＝1,2,
…
,9。
[0235]
图2、3分别为经过本发明控制方法机械臂末端x轴跟踪曲线与跟踪误差图，图4、5分别为经过本发明控制方法机械臂末端y轴跟踪曲线与跟踪误差图。
[0236]
由图2-5可知，本发明控制方法能够使机械臂末端快速精确地跟上期望轨迹。
[0237]
图6、7分别为本发明控制方法机械臂末端x轴方向力跟踪图与力跟踪误差图，图8、9分别为本发明控制方法机械臂末端力y轴方向力跟踪图与力跟踪误差图。
[0238]
由图6-9可知，本发明控制方法能够使机械臂末端的接触力很好地跟上期望接触力。
[0239]
图10为本发明控制方法二关节机械臂各关节力矩图。
[0240]
在图10中，τ1为机械臂第1关节力矩，τ2为机械臂第2关节力矩。
[0241]
以上模拟信号清楚地表明，本发明提出的基于有限时间输出状态受限的多关节机械臂阻抗控制方法，能够在保证系统安全的前提下，高效地跟踪机械臂期待轨迹。
[0242]
当然，以上说明仅仅为本发明的较佳实施例，本发明并不限于列举上述实施例，应
当说明的是，任何熟悉本领域的技术人员在本说明书的教导下，所做出的所有等同替代、明显变形形式，均落在本说明书的实质范围之内，理应受到本发明的保护。