一种水下机器人-机械手系统受海流扰动强弱评估方法与流程

[0001]
本发明涉及机器人控制领域，尤其涉及一种水下机器人-机械手系统受海流扰动强弱评估方法。


背景技术：

[0002]
扰动补偿控制在控制领域尤其是水下机器人领域是必不可少的技术。在复杂的海洋环境下，如海流涌动的航道，由于海流海浪的影响，使得水下机器人的工作位姿很容易发生偏移。而且相对于陆地来说，海洋环境更加复杂多变，海流海浪是水下环境不可避免的一部分，所以水下机器人-机械手系统(underwater vehicle-manipulator system,uvms)在进行抓取工作时，会受到海浪海流影响，产生水下机器手偏移，影响机械手末端相对目标物位置，进而影响抓取的准确度。而当海浪海流影响较大时，使水下机器人本体发生较大偏移，由于水下机器人与机械手之间的耦合关系，机械手末端也将发生严重偏移，进而影响抓取的准确度。
[0003]
魏延辉等人提出了一种近海面条件下的利用多传感器信息融合的海浪对水下机器人扰动评估方法，作者采用惯导系统、水下摄像头、声学测距传感器等采集本体航向姿态、水下目标物图像位置、水下机器人相对距离变化等综合信息，并将这些信息数据融合处理，从而掌握海流对水下机器人扰动的影响量级，为水下机器人控制研究提供扰动量，但未研究水下机器人抓取任务中机械手末端所受扰动强弱，无法为水下机械手在海流扰动环境下的控制研究提供扰动量。本发明参考魏延辉提出的扰动评估方法，对执行抓取工作的水下机器人受海流海浪扰动强弱进行分级讨论，对机械手末端相对目标物偏移量分析，将扰动情况分为强扰动与弱扰动，针对不同的扰动等级进行不同的补偿控制；弱扰动情况下对机械手关节进行补偿控制，使机械手末端再次与目标物重合，提高抓取任务成功率；若扰动为强扰动，此时由于机械手关节转角大小的限制，仅对机械手关节进行补偿控制已不能实现末端与目标物的重合，需对水下机器人本身控制，将强扰动造成的影响削弱，使扰动等级变为弱扰动后在对机械手关节进行补偿控制，最终实现不同扰动等级下控制策略。


技术实现要素：

[0004]
根据现有技术存在的问题，本发明公开了一种水下机器人-机械手系统受海流扰动强弱评估方法，包括以下步骤：
[0005]
s1:当水下机器人-机械手系统到达海底任务位置，将受扰动后机器人的机械手实际位姿与理想状态下位姿进行对比，得到机械手在物理空间上的受扰动位置的变化；
[0006]
s2:将机械手在物理空间上的位置的变化划分为水下机器人本体在x-y平面受侧向横移扰动y
d
、艏向扰动ψ
d
的时位置变化及x-z平面受升降扰动位置变化，
[0007]
当水下机器人本体在x-y平面受侧向横移扰动y
d
、艏向扰动ψ
d
发生位置变化时，对机械手第一关节进行补偿，使第一关节绕z轴转动，使机械手末端回到期望情况下末端位置，得到为x-y平面上补偿后机械手末端与期望情况下机械手末端夹角r
z
；
[0008]
当水下机器人本体在x-z平面受升降扰动发生位置变化，对机械手第二、三关节进行补偿，使机械手第二、三关节绕y轴转动，使进而机械手末端回到期望情况下末端位置，得到x-z平面上补偿后机械手末端与期望情况下机械手末端夹角r
y
；
[0009]
s3:当补偿后机械手末端与期望情况下末端z轴方向夹角r
z
＞阈值ⅰ，则水下机器人-机械手系统x-y平面受到的扰动为强扰动；
[0010]
当补偿后机械手末端与期望情况下末端z轴方向夹角r
z
≤阈值ⅰ，则水下机器人-机械手系统x-y平面受到的扰动为弱扰动；
[0011]
当补偿后机械手末端与期望情况下末端y轴方向夹角r
y
＞阈值ⅱ，则水下机器人-机械手系统x-z平面受到的扰动为强扰动；
[0012]
当补偿后机械手末端与期望情况下末端y轴方向夹角r
y
≤阈值ⅱ，则水下机器人-机械手系统x-z平面受到的扰动为弱扰动；
[0013]
当水下机器人-机械手系统x-y平面受到的扰动为弱扰动和x-z平面受到的扰动为弱扰动时，则水下机器人-机械手系统受到的海流扰动等级为弱扰动；其余情况下则水下机器人-机械手系统受到的海流扰动等级为强扰动。
[0014]
进一步地：所述r
z
的表达式如下：
[0015][0016]
其中：l1、l2、l3为机械手第一关节、第二关节和第三关节的长度，y
d
为x-y平面侧向横移扰动，l为x方向水下机器人重心与机械手第一关节间距离，θ
2r
为补偿后机械手第二节与第一节延长线夹角，ψ
d
为x-y平面横向扰动。
[0017]
进一步地：
[0018][0019]
其中：z
d
为x-z平面升降扰动。
[0020]
进一步地，该方法适用于三关节的机器人-机械手，机器人-机械手的第一关节坐标系固定在水下机器人上，第一关节的转动轴与水下机器人-机械手系统载体坐标系中的z轴平行，第二关节、第三关节转动轴与水下机器人-机械手系统载体坐标系中的y轴平行。
[0021]
进一步地，所述阈值ⅰ和阈值ⅱ为
[0022]
由于采用了上述技术方案，本发明提供的一种水下机器人-机械手系统受海流扰动强弱评估方法，对水下机械手尤其是机械手末端受海流扰动情况做了重点讨论，将扰动模型简化，对水平面(x-y)与竖直面(x-z)分别讨论，可为控制策略中的扰动提供参考，进而提高抓取的准确性,该评估方法与水下机器人运动特征相符合，水下机器人的六自由度运动模型可简化为x-y平面与x-z平面的二维运动模型，同样的任务背景下，所需控制系统复杂度更低。
附图说明
[0023]
为了更清楚地说明本申请实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本申请中记载的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。
[0024]
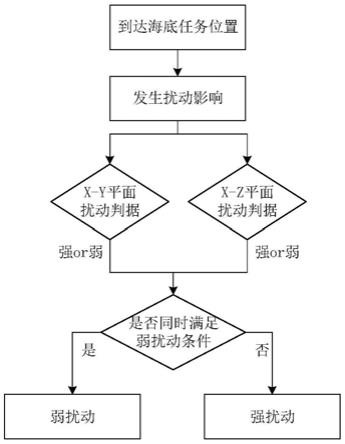
图1为本方法的总体流程图；
[0025]
图2为机械手标准d-h坐标系示意图；
[0026]
图3为机械手matlab可视化模型图；
[0027]
图4为水下机器人-机械手系统三维模型示意图；
[0028]
图5为水下机器人-机械手系统运动学模型示意图；
[0029]
图6为期望状态下的坐标系简化图；
[0030]
图7为x-y平面扰动示意图；
[0031]
图8为x-z平面扰动示意图；
[0032]
图9为x-y平面扰动补偿示意图；
[0033]
图10为x-z平面扰动补偿示意图。
具体实施方式
[0034]
为使本发明的技术方案和优点更加清楚，下面结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚完整的描述：
[0035]
水下机器人-机械手系统的工作特点在于：当机械手末端到达目标物位置时，由于海流等扰动情况存在，导致机械手末端无法稳定到抓取任务结束。根据水下机器人-机械手系统的上述特点，通过对扰动前后机械手的位姿比较，对海流海浪造成的扰动强弱等级进行讨论，为不同扰动等级下的控制策略提供参考。
[0036]
本发明是基于一种三关节的水下机械手，根据表1中标准d-h坐标系的建立方法和规则，传接各个连杆相应的坐标系。
[0037]
表1 d-h参数定义表
[0038][0039][0040]
机械手安装于水下机器人前方，机械手第一关节坐标系(机械手基座坐标系)固定
在水下机器人上，其转动轴与水下机器人载体坐标系中的z轴平行，使第一关节可以在水下机器人艏向转动。第二关节、第三关节转动轴与水下机器人载体坐标系中的y轴平行，机械手末端坐标系建立在机械手第三连杆上；水下机器人的载体坐标系以机器人重心为原点，其中x轴为水下机器人运动方向，z轴方向与重力方向一致，y轴通过机器人右手定则确立。根据物理量与初始位置，可得到机械手的d-h参数表，如表2。
[0041]
表2 机械手d-h参数表
[0042][0043]
为验证d-h参数的准确性，依靠matlab软件中的机器人工具包(robotic toolbox)，对连杆关节编写代码，进行可视化验证，运行后得到示意图图1。
[0044]
图2为本方法的总体流程图；一种水下机器人-机械手系统受海流扰动强弱评估方法，包括以下步骤：
[0045]
s1:当水下机器人-机械手系统到达海底任务位置时，将受扰动后机器人的机械手实际位姿与理想状态下位姿进行对比，得到机械手在物理空间上的受扰动位置的变化；
[0046]
在机器人控制领域中，运动学建模的主要方法是denavit-hartenberg(d-h)法，如图3所示，以连杆输出端建立坐标系，并且建立相应的坐标系变换矩阵。连杆i为坐标系{i}，其中轴z
i-1
为连杆i-1与连杆i旋转轴，连杆参数定义如表1所示。相邻坐标系之间的转换关系可以理解为：使x
i-1
与x
i
平行时先使坐标系{i-1}绕着z
i-1
旋转θ
i
，再沿着z
i-1
方向移动d
i
从而使x
i-1
与x
i
共线，然后沿着x
i-1
移动a
i
，此刻两坐标系{i-1}与{i}原点重合，最后绕x
i-1
旋转α
i
使两坐标系完全重合，此刻完成相邻坐标系之间的转换。
[0047]
由于水下机械手并不是固定不动的，而是安装在水下机器人平台上，因此还需建立其与水下机器人的联系。为直观的表现，采用三维建模软件solid works，建立水下机器人-机械手系统三维模型，如图4所示。各关节坐标系间关系如图所示5，其中l
i
表示连杆i的长度，x
i
代表坐标系{i+1}在坐标系{i}下x轴方向，z
i
代表连杆i与连杆i+1的旋转轴方向；建立正运动学模型可得机械手末端在固定坐标系下坐标如下式所示：
[0048][0049]
[0050][0051]
其中:x
b
、y
b
、z
b
为机械手基座在水下机器人的载体坐标系下的坐标，其中x、y、z为水下机器人在固定坐标系下的坐标，θ、ψ分别代表水下机器人的横摇、俯仰和偏航角度，l1、l2、l3与θ1、θ2、θ3分别代表机械手对应手臂长度与关节角度。
[0052]
s2:将机械手在物理空间上的位置的变化划分为水下机器人本体在x-y平面受侧向横移扰动y
d
、艏向扰动ψ
d
的时位置变化及x-z平面受升降扰动位置变化，
[0053]
当水下机器人本体在x-y平面受侧向横移扰动y
d
、艏向扰动ψ
d
发生位置变化时，对机械手第一关节进行补偿，令第一关节绕z轴转动，使机械手第一段与x轴夹角θ
1r
增大、机械手第二段与第一段延长线夹角θ
2r
与机械手第三段与第二段延长线夹角θ
3r
保持为零，使机械手末端回到期望情况下末端位置，得到为x-y平面上补偿后机械手末端与期望情况下机械手末端夹角r
z
；
[0054]
当水下机器人本体在x-z平面受升降扰动发生位置变化，对机械手第二、三关节进行补偿，使机械手第二、三关节绕y轴转动，保持θ
1r
不变，使θ
2r
、θ
3r
增大，进而机械手末端回到期望情况下末端位置，得到x-z平面上补偿后机械手末端与期望情况下机械手末端夹角r
y
；
[0055]
扰动情况强弱的判断需要先确定水下机器人-机械手系统的期望运动状态；当机械手末端到达目标物位置时，不考虑扰动情况下，由于目标物位置已知，此时水下机器人的期望位姿、机械手关节期望角度均唯一确定。图6为期望状态下的工作场景坐标体系简化图，可知期望状态时，机械臂第一、三关节处于平行状态，为保证机械手关节最大调整范围，此时满足下式。
[0056]
θ
2r
＝θ
2r
＝θ
3r
＝0
ꢀꢀꢀ
(4)
[0057]
实际工作场景中水下机器人时刻处于受扰动状态，本发明涉及的水下机械手安装于水下机器人平台上，发生在水下机器人本身的扰动会对机械手末端位姿产生巨大影响。水下机器人具有六自由度运动的同时，也存在六自由度的扰动。但水下机器人运动具有特殊性，不易发生仰俯与侧倾，可将其运动简化为两平面内的运动，分别为水下机器人水平面(x-y面)与竖直面(x-z面)。
[0058]
s2:将机械手在物理空间上的位置的变化划分为水下机器人本体在x-y平面受侧向横移扰动y
d
、艏向扰动ψ
d
的时位置变化及x-z平面受升降扰动位置变化，
[0059]
当水下机器人本体在x-y平面受侧向横移扰动y
d
、艏向扰动ψ
d
发生位置变化时，对机械手第一关节进行补偿，使第一关节绕z轴转动，使机械手末端回到期望情况下末端位置，得到为x-y平面上补偿后机械手末端与期望情况下机械手末端夹角r
z
；
[0060]
当水下机器人本体在x-z平面受升降扰动发生位置变化，对机械手第二、三关节进行补偿，使机械手第二、三关节绕y轴转动，使进而机械手末端回到期望情况下末端位置，得到x-z平面上补偿后机械手末端与期望情况下机械手末端夹角r
y
；
[0061]
图7为x-y平面扰动示意图，即横移扰动y
d
、艏向扰动ψ
d
示意图，当水下机器人相对期望状态发生横向扰动ψ
d
时，使机械手末端在z轴产生角度偏差，并沿y轴方向发生偏差y
e1
,当水下机器人相对期望状态发生横移扰动y
d
时，使机械手末端y轴方向发生偏差y
e2
；
[0062]
图8为x-z平面扰动示意图，即升降扰动z
d
示意图。当水下机器人相对期望状态发生升降扰动z
d
时，使机械手末端z轴方向发生偏差z
e
。
[0063]
以上所述的扰动情况有强弱等级的区别，当扰动情况过强时，无法通过控制机械手关节使末端满足工作需求时，需要对水下机器人进行控制，以下将对强弱等级评估方法进行详细说明。
[0064]
s3:由于横移扰动y
d
、艏向扰动ψ
d
均发生在x-y平面，故对两者同时分析，此情况下只能对机械手第一关节进行补偿，使第一关节绕z轴转动，进而机械手末端回到期望情况下末端位置。如图9所示，其中r
z
为补偿后机械手末端与期望情况下末端z轴方向夹角，是x-y面上强弱扰动判据核心。
[0065]
当只对机械手第一关节进行补偿，若机械手末端可以回到期望情况下末端位置，则此时发生的扰动为x-y面上的弱扰动，根据图9，弱扰动情况下需满足否则无法只对机械手第一关节补偿达到目的，从而扰动等级为强。其中为经验值，与水下机器人摄像头参数信息有关。
[0066]
根据图9与三角函数公式可得到如下关系：
[0067][0068]
化简后得
[0069][0070]
即：当补偿后机械手末端与期望情况下末端z轴方向夹角则水下机器人-机械手系统x-y平面受到的扰动为弱扰动；
[0071]
当补偿后机械手末端与期望情况下末端z轴方向夹角则水下机器人-机械手系统x-y平面受到的扰动为强扰动，此时需要控制水下机器人在x-y平面上运行进行补偿，满足时只需控制机械手第一关节；
[0072]
升降扰动z
d
发生在x-z平面，此情况下只能对机械手第二、三关节进行补偿，使其绕y轴转动，进而机械手末端回到期望情况下末端位置。如图10所示，其中r
y
为补偿后机械手末端与期望情况下y轴末端夹角，是x-z面上强弱扰动判据核心。此时同样需满足当第二第三连杆拉直时，达到最大调节位置，根据图10与三角函数公式可得到如下关系：
[0073][0074]
化简后得：
[0075]
[0076]
即当补偿后机械手末端与期望情况下末端y轴方向夹角则水下机器人-机械手系统x-z平面受到的扰动为弱扰动；
[0077]
当补偿后机械手末端与期望情况下末端y轴方向夹角则水下机器人-机械手系统x-z平面受到的扰动为强扰动；需要控制水下机器人在x-z平面上运动进行补偿，满足时只需控制机械手第二关节和第三关节。
[0078]
由上可得：当水下机器人-机械手系统x-y平面受到的扰动为弱扰动和x-z受到的扰动等级为弱扰动时，则水下机器人-机械手系统受到的海流扰动为弱扰动；其余情况下则水下机器人-机械手系统受到的海流扰动等级为强扰动，即只要当水下机器人-机械手系统无论x-y平面受到的扰动为强扰动还是x-z平面受到的扰动为强扰动，则水下机器人-机械手系统受到的海流扰动等级为强扰动。
[0079]
当水下机器人-机械手系统受到的海流扰动等级为弱扰动时，既只通过调节机械手关节角度便可使扰动后机械手末端回到期望位置，需要同时满足式(6)(8)。若不同时满足式，则扰动等级为强扰动，此刻无法通过调节机械手关节角度使扰动后机械手末端回到期望位置，需要进一步控制水下机器人本体的运动。由此提出一种水下机器人-机械手系统受海流扰动强弱评估方法，可为其水下机器人-机械手系统抓取任务情境下的控制策略提供参考。
[0080]
以上所述，仅为本发明较佳的具体实施方式，但本发明的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本发明揭露的技术范围内，根据本发明的技术方案及其发明构思加以等同替换或改变，都应涵盖在本发明的保护范围之内。