一种基于值迭代的Baxter机械臂智能优化控制方法

本发明属于控制技术领域，具体提供一种基于值迭代的baxter机械臂智能优化控制方法，实现系统模型未知情况下的baxter机械臂系统的最优控制。

背景技术：

多轴机械臂因其独特的设计结构，能够在多个领域得到广泛的推广使用，采用工业机械臂代替人力所要完成的任务，可以提升工业生产、加工的自动化水平，因此机械臂技术的突破及产业的拓展意义重大。

控制系统传统的开发流程一般以数学仿真为主，数学仿真对于baxter机械臂这一类非线性强耦合度的被控对象实现起来较为困难，并且此类仿真的结果置信度较低，往往难以达到预期效果。同时，目前对于多轴机械臂的控制研究，多采用传统的基于模型的控制方法，未能利用数据驱动思想在线实现对系统的控制，需要完全已知系统模型。而baxter机械臂由于模型参数未知，可使用的传统的基于模型的控制方法更加有限，通过系统辨识对baxter机械臂进行建模，工作量巨大且需要耗费大量时间和精力，同时可能存在模型不匹配、未建模动态等问题。

技术实现要素：

为了克服现有方法存在不足，本发明提供一种基于值迭代的baxter机械臂智能优化控制方法，该方法提出一种基于自适应值迭代算法，将adp和智能优化控制系统理论的概念结合起来，提出了一种在线adp技术，它能以时间向前的方式解决具有未知动力学参数的系统的连续时间无限时域最优控制问题；据测量控制器性能的信号序列更新控制器参数，通过更新控制策略和值函数估计的迭代过程，使它们接近最优控制策略和相应的最优值函数；每个迭代步骤包括基于当前控制策略的值函数更新，以及基于新的值函数估计值更新控制策略。

本发明解决其技术问题所采用的技术方案是：

一种基于值迭代的baxter机械臂智能优化控制方法，考虑baxter机械臂系统动力学方程如下：

其中q,分别表示机械臂位置，角速度，角加速度向量，mj(q)表示机械臂惯性矩阵，cj表示机械臂科氏力矩向量,gj(q)表示机械臂重力矩向量，τ表示机械臂控制力矩向量，τd表示外部环境的未知扰动力矩向量；

系统状态向量由下式表示：

baxter机械臂的状态空间方程给出如下：

其中，u＝τ为系统力矩输入，为状态向量，y为输出，矩阵ac,bc,hc定义如下：

其中，on为(n×n)的零矩阵，in为(n×n)的单位矩阵；

其中，0n为(n×1)的零矩阵，n(x1,x2)收集科式力矩、重力矩相关信息；

对于q-learning值迭代最优控制问题：

有限域最优控制问题为：

选取q＝1，r＝1，(a,b)能控，控制器的求解由贝尔曼最优原理确认，由u＝-kx，其中k＝r^-1b^th，且h满足代数黎卡提方程：

a^th+ha-hbr^-1b^th+q＝0(8)

所述智能优化控制方法包括以下步骤：

步骤1)对系统进行初始化处理，步骤如下：

1.1)选取基函数：对连续时间lqr，其值函数在状态下是二次的，因此，选择(9)式中的actor神经网络的基函数作为状态分量的二次多项式向量，该向量状态个数为n，则该基函数含有n(n+1)/2个分量，同时，权重向量w由矩阵h中的元素组成；

1.2)初始化系统：选择初始状态x0，计算基函数初始值，确定初始策略k0；

步骤2)对系统进行采样，并进行最小二乘法的计算，求得最优值函数,即策略评估过程；为了得到在策略ki下每一步的q函数，使用参数矩阵hi计算，记上述公式变为：

其中为kronecker内积二次多项式基向量，元素为{zi(t)zj(t)}i＝1,n；j＝i,n，为向量值矩阵函数，作用于n×n矩阵，通过将对称矩阵的元素叠加成一个向量，非对角元素求和为hij+hji，从而得到列向量；

在每个迭代步骤中，在使用相同的控制策略ki收集足够数量的位置和角速度轨迹点后，用最小二乘法求解q函数参数从而得到hi+1，在最小平方意义下，通过最小化目标函数之间的误差来找到参数向量h的最小值，在状态空间中n>n(n+1)个点zi求值，得到最小二乘解为:

其中，

测量时间t和t+t离散时刻的状态，以及在采样时间间隔内观察到的奖励：

hi+1＝f(hi+1)(15)

步骤3)根据得到的最优值函数，通过贪心算法更新最优参数：

当最小二乘法收敛时，策略不再更新，得到最优策略，连续时间adp算法由(14)和(6)之间的迭代组成，然而，使用(15)更新控制策略不需要包含动力学知识的系统矩阵，这使得算法在无模型的情况下实现。

本发明的工作原理如下：初始化系统，确定系统能控；对系统进行采样，使用最小二乘法在线计算值函数进行策略评估，当取得最优值函数时使用贪心算法更新策略，最终得到最优策略。

所用机器人平台为baxter机器人，baxter机器人是美国rethinkrobotics公司研发的一款双臂机器人，其单机械臂是一种具有七自由度的冗余柔性关节机械臂。通过移动底座支撑机器人本体，机器人手臂采用旋转关节连接刚性连杆，关节处采用弹性制动器连接，即通过电机、减速器串联弹簧带动负载，在人机协作或外部冲击下起到保护人或机器人本体的作用。柔性关节还可通过霍尔效应检测角度偏差。在baxter关节处都具有力矩传感器。手臂前后端通过26w和63w伺服电机驱动，通过14bit编码器实现关节角度的读取。baxter机器人为基于ros(robotoperatingsystem)操作系统的开源机器人，通过linux平台运行,用户可通过网络与机器人内部计算机互联读取信息或发送指令，或通ssh(secureshell)远程控制在内部计算机运行相关程序。利用baxter相关的sdk(softwaredevelopmentkit)，通过ros的api(applicationprogramminginterface)可以实现对baxter机器人的信息读取与实时控制。baxter中的sdk可以提供相关函数接口与重要工具：如gazebo仿真器及moveit移动软件包等。

本发明的有益效果为：通过值迭代的自适应控制，求解最优控制策略来实现对系统进行智能优化控制，在系统部分模型参数未知的情况下，不需要对系统进行辨识，而是基于值迭代的自适应控制方法，在线对系统实现最优控制,同时在机器人平台进行算法调试，在实际层面实现效果。

附图说明

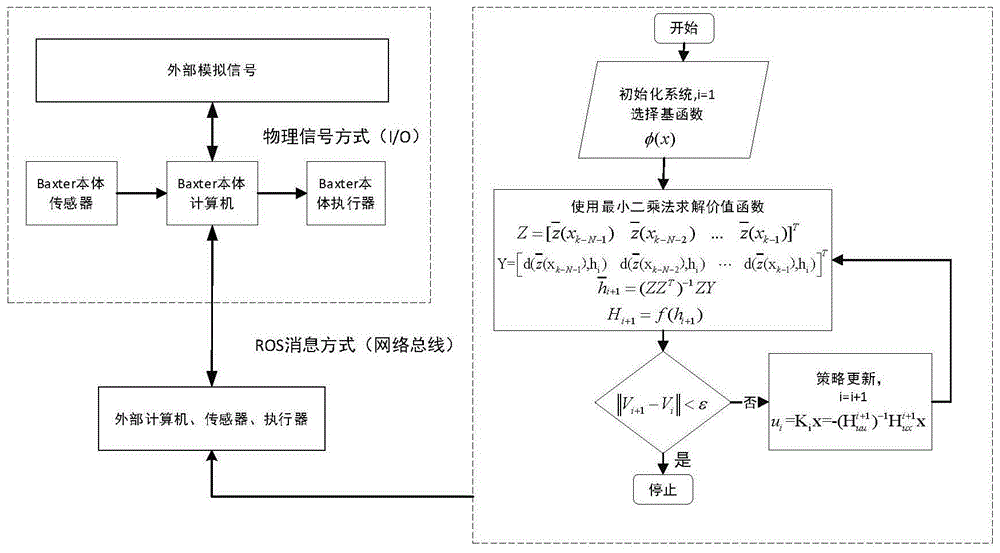
图1是一种基于值迭代的baxter机械臂智能优化控制方法的流程图；

图2是基于值迭代自适应控制的系统位置和角度变化图；

图3是基于值迭代和任意给定策略控制下的性能指标对比图；

图4是基于策略迭代下的系统输入变化图。

具体实施方式

为了让本方案的技术特点、目的和优点更加清晰、明朗，下面结合附图和实际实验对本发明的技术方案作进一步描述。

参照图1～图4，一种基于值迭代的baxter机械臂智能优化控制方法，先初始化baxter机械臂系统，选择基函数；对系统状态及输入进行采样，由当前时刻状态计算下一时刻状态，在线计算最优值函数；在得到最优值函数后，利用贪心算法更新策略，策略收敛时达到最优，不再更新，从而实现对系统的最优控制。

本发明为一种基于值迭代的baxter机械臂智能最优控制方法,包括以下步骤：

1)初始化系统，选择基函数；

2)对系统进行采样,收集输入输出数据；使用最小二乘法计算值函数最优值，进行策略评估；

3)使用贪心算法更新策略。

进一步，所述步骤1)中，考虑三关节baxter机械臂系统如下：

其中bc,ηc未知，取q＝1，r＝1。

实验基于值迭代的自适应控制算法，通过获取采集机械臂位置和角速度，控制算法中策略的评估与更新中不涉及包含动力学知识的矩阵的使用，q1指机械臂一关节位置，指机械臂一关节角速度。对系统进行初始化，取初始状态x0＝[111111]^t,选择基函数

再进一步，所述步骤2)中，任意给定某个策略，对系统进行策略评估和策略提升：

2.1)策略评估：在给定初始策略k0＝o3×6的情况下，取采样时间t＝0.004s，在有限区间[t,t+t]上对系统进行采样，利用当前时刻机械臂的位置和角速度x(t)，更新下一时刻位置和角速度x(t+t),使用最小二乘法进行值函数计算，机械臂位置和角速度变化、价值函数变化如图2、图3所示；2.2)策略提升：经过策略评估后，得到最优值函数，利用贪心算法进行策略更新，当策略不随时间而变化时，得到最优策略。

从实验结果图3来看，策略更新60次后策略收敛不再更新，机械臂关节速度最终收敛接近于0，其控制效果可以达到预期要求。

在与已知动力学模型，任意给定策略的情况下的对比中，图3说明本方法系统状态收敛平缓快速，且过程中未出现过大超调量，可以实现预期控制效果在图4中的性能指标对比中可以发现，本方法可以更好更快地取得最佳性能指标。

本发明提供了一种基于值迭代的多轴机械臂智能优化控制方法，使用值迭代的自适应控制方法，经过策略评估和策略提升两个步骤实现在线解决系统最优控制问题，与现有技术相比，本发明的实用性在于：不需要系统模型参数进行辨识，可以通过采集系统轨迹数据获取系统信息，从而获得最优控制策略；通过baxter机器人平台调试，实现本方法在实际平台的良好控制。

以上结合附图详细阐述了本发明的技术方案但并不局限于此，在本领域的技术人员所具备的知识范围内，只要以本发明的构思为基础，还可以做出多种变化和改进。