一种人机协作装配中的机器人位姿标定方法

1.本发明属于机器人技术领域，具体涉及一种机器人位姿标定方法。


背景技术：

2.目前，人机协作装配方式由于其灵活的、半自动化的高效生产方式正在被广泛地应用在许多行业的焊接、装配和搬运等工作中。人机协作装配可以将人类和机器人的优势充分发挥出来并且补足对方的短板，协作机器人可以分担工作量从而降低工人劳动强度，工人可以处理一些柔性部件并且应对复杂的工况，弥补机器人在这些方面的不足，这种人机协作的生产方式已经成为未来制造业领域中一个新的发展方向。
3.机器人与工件的标定是机器人进行后续工作的前提，其目的是获取工件在机器人坐标系下的位姿信息，标定的精度直接影响了机器人的工作精度。传统的工业机器人标定时通常选择机器人末端工具与基准点的之间的点对点接触模式进行标定工作，但在人机协作装配中，由于人在拖动机器人手臂时会发生抖动，使得操作人员需要较长的时间才能完成点对点的高精度重合，严重制约了标定效率。因此在人机协作工作时迫切需要一种高效、简便和高精度的协作机器人位姿标定方法。


技术实现要素：

4.为了克服现有技术的不足，本发明提供了一种人机协作装配中的机器人位姿标定方法，首先根据工件基准孔特征选用合适的半球形探针工具和标定工装来标定出机器人tcp点；再从所建立的工件三维模型中提取n个大小相同的基准孔中心点的坐标得到基准孔坐标数据集；然后机器人运动使得探针与选取的基准孔紧密接触，利用机器人的当前位姿得到对应的机器人基坐标系下的tcp点集；最后对数据集进行去中心化处理，通过数据有效性评价最终获得工件坐标系到机器人基坐标系的最优变换。本发明将过去传统标定时机器人末端工具与基准点的点对点接触模式转变为线对面的接触模式，大大减轻操作人员手工拖动机器人进行标定的负担，提升了协作机器人位姿标定效率并保证了标定精度。
5.本发明解决其技术问题所采用的技术方案包括如下步骤：
6.步骤1：根据工件的基准孔特征选取探针工具和标定工装，将探针工具安装在机器人上，使用标定工装标定出探针工具的探头球心tcp点坐标和工具坐标系tcf；
7.步骤2：从工件三维模型中提取n个大小相同的基准孔，基准孔的中心点在工件坐标系的坐标构成基准孔坐标数据集p
a
(p1,p2,
…
,p
n
,n≥3)；
8.步骤3：机器人运动使探针工具的探头与步骤2中提取的基准孔逐个紧密接触，记录在当前机器人基坐标系下tcp点的坐标，构成数据点集p
b
；
9.步骤4：将基准孔坐标数据集p
a
和数据点集p
b
代入工件坐标系到机器人基坐标系的坐标转换方程中，构成超定方程组；
10.采用加权最小二乘法求解超定方程组的最优解，并利用奇异值分解求得工件坐标系到机器人基坐标系的坐标转换方程的系数：旋转矩阵r和平移向量t；
11.步骤5：检测基准孔坐标数据集p
a
、数据点集p
b
、旋转矩阵r和平移向量t的数据有效性并通过工件平面法向量及工件基准孔坐标偏差进一步精确工件在机器人基坐标系下的表示，完成机器人的位姿标定。
12.进一步地，所述步骤1具体如下：
13.步骤1
‑
1：根据工件基准孔的大小选择匹配的含有半球形探头的探针工具和标定工装，所述半球形探头能够伸入工件的基准孔和标定工装的标定孔但不能全部进入，所述标定工装上的标定孔与工件基准孔的孔径大小一致；
14.步骤1
‑
2：将半球形探头从四个不同的方向贴合标定工装上的同一个标定孔，利用机器人法兰位置不同的坐标值计算出探头球心tcp点的坐标并作为工具坐标系的原点；
15.步骤1
‑
3：标记探针工具轴线的平行线，利用两点世界坐标系法标定工具坐标系的x轴方向，工具坐标系的三个坐标轴的方向均与机器人末端法兰坐标系保持一致，完成机器人的工具坐标系tcf的标定。
16.进一步地，所述步骤2具体如下：
17.步骤2
‑
1：建立工件的三维数学模型，并以工件的一个角为原点建立工件坐标系；
18.步骤2
‑
2：在工件坐标系中，通过solidworks测量工具导出所有基准孔中心点坐标并选取其中n个大小相同的基准孔中心点的坐标得到基准孔坐标数据集p
a
。
19.进一步地，所述步骤4具体如下：
20.步骤4
‑
1：利用数据集质心求解公式求解数据集p
a
的质心centroid
a
和数据集p
b
的质心centroid
b
，再进行去中心化处理，分别将数据集p
a
和数据集p
b
的所有点跟随各自的质心移动，将各自的质心移动至自身所在坐标系的原点处；
21.步骤4
‑
2：采用加权最小二乘法求解超定方程组的最优解，并利用奇异值分解求解工件坐标系到机器人基坐标系的坐标转换方程的系数：旋转矩阵r和平移向量t；
22.步骤4
‑2‑
1：将工件坐标系到机器人基坐标系的坐标转换方程的系数：旋转矩阵和平移向量分别记作(r,t)；
23.任意一对数据集p
a
中的点p
i
和数据集p
b
中的点q
i
均满足工件坐标系到机器人基坐标系的坐标转换方程q
i
＝r
·
p
i
+t；
24.将基准孔坐标数据集p
a
和数据点集p
b
代入工件坐标系到机器人基坐标系的坐标转换方程中，构成超定方程组；
25.步骤4
‑2‑
2：利用最小二乘法对超定方程组求最优解的问题描述为：
[0026][0027]
其中w
i
为第i对点(p
i
,q
i
)的权重且w
i
>0；
[0028]
步骤4
‑2‑
3：假设r为常值，令：
[0029][0030]
对t求导得到：
[0031][0032]
进一步得到：
[0033][0034]
从而：
[0035][0036]
其中x
i
和y
i
分别表示p
i
和q
i
去中心化并跟随质心移动至自身所在坐标系的原点后的坐标；
[0037]
由于：
[0038][0039]
且由于和为常数，因此得到：
[0040][0041]
式中w是由w
i
组成的n
×
n对角阵，x和y分别是由x
i
和y
i
组成的3
×
n的矩阵；对xwy
t
做奇异值分解得到此时其中d＝v
t
ru；u和v是xwy
t
做奇异值分解得的矩阵，σ为xwy
t
的奇异值构成的对角矩阵；
[0042]
由于σ为奇异值构成的对角矩阵，d为正交矩阵，由正交矩阵性质得到：
[0043][0044]
其中σ
i
表示xwy
t
的各奇异值；
[0045]
步骤4
‑2‑
4：由式(3)，当d＝i时，tr(∑d)取得最大值，即求得最优的正交矩阵：
[0046][0047]
当的行列式为
‑
1时，该结果被排除，需要寻找次优解，此时最优旋转矩阵r表示
为：
[0048][0049]
将式(4)代入t＝centroid
b
‑
r
·
centroid
a
即求得平移向量t；
[0050]
进一步地，所述步骤5具体如下：
[0051]
步骤5
‑
1：从数据集p
a
中选取m个点代入q
i
＝r
·
p
i
+t中，得到机器人基座标下的理论tcp点的坐标q
i
′
，使用公式(5)进行评价：
[0052][0053]
式中δ为tcp点坐标误差，γ表示孔坐标测量误差阈值；若误差δ大于阈值γ，则判定数据检测有误，重复步骤1到步骤4重新计算旋转矩阵r和平移向量t；若误差δ小于等于阈值γ，则判定基准孔坐标数据集p
a
、数据点集p
b
、旋转矩阵r和平移向量t有效；
[0054]
步骤5
‑
2：从数据集p
a
中取任意三个中心不共线的基准孔a、b、c，假设a、b、c三点的坐标分别为a(x
a
,y
a
,z
a
)、b(x
b
,y
b
,z
b
)、c(x
c
,y
c
,z
c
)，由于工件法向与基准孔所在平面垂直，利用a、b、c三个点组成的任意两个向量，求出基准孔所在平面的法向值
[0055]
已知半球形探头半径为基准孔内径为r；通过工件坐标系到机器人基坐标系的坐标转换方程计算出工件上的任意点p在机器人基坐标系下对应的坐标p'，再通过式(6)计算经过补偿后工件上的任意点p在机器人基坐标系中的坐标p”：
[0056][0057]
其中d为工件基准孔中心测量坐标与实际坐标之间的固定偏差。
[0058]
本发明的有益效果如下：
[0059]
1.针对人手动拖动协作机器人进行标定时会产生抖动以至于难以完成点对点标定工作的问题，本发明利用半球形探针工具和专用标定工装，将过去传统标定时机器人末端工具与基准点的点对点接触模式转变为线对面的接触模式，大大减轻操作人员手工拖动引导机器人进行标定的负担，提升标定速度并保证了标定精度。
[0060]
2.本发明所用的的标定工具包括半球形探针工具和专用标定工装，标定工具成本低；标定过程简单，能够进一步提高本方法的实用性和便利性；
[0061]
3.本发明对任何人机协作机器人的标定工作均适用，只需根据工件基准孔大小选择合适的半球形末端探针和标定孔大小合适的标定工装即可，进一步提高本标定方法的实用性。
附图说明
[0062]
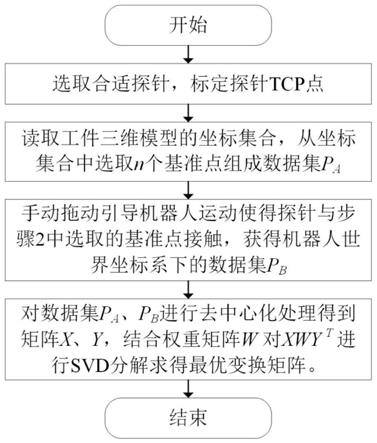
图1是本发明的机器人位姿标定方法流程图。
[0063]
图2是本发明机器人基坐标系、工具坐标系、法兰坐标系和工件坐标系示意图。
[0064]
图3是本发明工具坐标系标定所需的半球形探针工具和专用标定工装示意图。
[0065]
图4是本发明工具坐标系标定时探针工具采用的四个姿态。
[0066]
图5是本发明数据集p
a
和p
b
去中心化过程示意图。
[0067]
图6是本发明tcp点与工件基准孔坐标位置关系示意图。
[0068]
图中：1
‑
工具坐标系，2
‑
工件坐标系，3
‑
法兰坐标系，4
‑
机器人基坐标系，5
‑
机器人，6
‑
半球形探针，7
‑
标定工装，8
‑
tcp点，9
‑
基准圆孔，10
‑
工件，11
‑
法向。
具体实施方式
[0069]
下面结合附图和实施例对本发明进一步说明。
[0070]
本发明提供了一种人机协作装配中的机器人位姿标定方法，将过去传统标定时机器人末端工具与基准点的点对点接触模式转变为线对面的接触模式，大大减轻操作人员手工拖动引导机器人的负担，极大提高了协作机器人位姿标定的效率并保证标定精度。
[0071]
如图1所示，一种人机协作装配中的机器人位姿标定方法，包括如下步骤：
[0072]
步骤1：根据工件的基准孔特征选取探针工具和标定工装，将探针工具安装在机器人上，使用标定工装标定出探针工具的探头球心tcp点坐标和工具坐标系tcf；
[0073]
步骤2：从工件三维模型中提取n个大小相同的基准孔，基准孔的中心点在工件坐标系的坐标构成基准孔坐标数据集p
a
(p1,p2,
…
,p
n
,n≥3)；
[0074]
步骤3：机器人运动使探针工具的探头与步骤2中提取的基准孔逐个紧密接触，记录在当前机器人基坐标系下tcp点的坐标，构成数据点集p
b
；
[0075]
步骤4：将基准孔坐标数据集p
a
和数据点集p
b
代入工件坐标系到机器人基坐标系的坐标转换方程中，构成超定方程组；
[0076]
采用加权最小二乘法求解超定方程组的最优解，并利用奇异值分解求得工件坐标系到机器人基坐标系的坐标转换方程的系数：旋转矩阵r和平移向量t；
[0077]
步骤5：检测基准孔坐标数据集p
a
、数据点集p
b
、旋转矩阵r和平移向量t的数据有效性并通过工件平面法向量及工件基准孔坐标偏差进一步精确工件在机器人基坐标系下的表示，完成机器人的位姿标定。
[0078]
进一步地，所述步骤1具体如下：
[0079]
步骤1
‑
1：根据工件基准孔的大小选择匹配的含有半球形探头的探针工具和标定工装，所述半球形探头能够伸入工件的基准孔和标定工装的标定孔但不能全部进入，所述标定工装上的标定孔与工件基准孔的孔径大小一致；
[0080]
步骤1
‑
2：将半球形探头从四个明显差异不同的方向贴合标定工装上的同一个标定孔，利用机器人法兰位置不同的坐标值计算出探头球心tcp点的坐标并作为工具坐标系的原点；
[0081]
步骤1
‑
3：标记探针工具轴线的平行线，利用两点世界坐标系法标定工具坐标系的x轴方向，工具坐标系的三个坐标轴的方向均与机器人末端法兰坐标系保持一致，完成机器人的工具坐标系tcf的标定。
[0082]
进一步地，所述步骤2具体如下：
[0083]
步骤2
‑
1：建立工件的三维数学模型，并以工件的一个角为原点建立工件坐标系；
[0084]
步骤2
‑
2：在工件坐标系中，通过solidworks测量工具导出所有基准孔中心点坐标并选取其中n个大小相同的基准孔中心点的坐标得到基准孔坐标数据集p
a
。
[0085]
进一步地，所述步骤4具体如下：
[0086]
步骤4
‑
1：利用数据集质心求解公式求解数据集p
a
的质心centroid
a
和数据集p
b
的质心centroid
b
，再进行去中心化处理，分别将数据集p
a
和数据集p
b
的所有点跟随各自的质心移动，将各自的质心移动至自身所在坐标系的原点处；
[0087]
步骤4
‑
2：采用加权最小二乘法求解超定方程组的最优解，并利用奇异值分解求解工件坐标系到机器人基坐标系的坐标转换方程的系数：旋转矩阵r和平移向量t；
[0088]
步骤4
‑2‑
1：将工件坐标系到机器人基坐标系的坐标转换方程的系数：旋转矩阵和平移向量分别记作(r,t)；
[0089]
任意一对数据集p
a
中的点p
i
和数据集p
b
中的点q
i
均满足工件坐标系到机器人基坐标系的坐标转换方程q
i
＝r
·
p
i
+t；
[0090]
将基准孔坐标数据集p
a
和数据点集p
b
代入工件坐标系到机器人基坐标系的坐标转换方程中，构成超定方程组；
[0091]
步骤4
‑2‑
2：利用最小二乘法对超定方程组求最优解的问题描述为：
[0092][0093]
其中w
i
为第i对点(p
i
,q
i
)的权重且w
i
>0；
[0094]
步骤4
‑2‑
3：假设r为常值，令：
[0095][0096]
对t求导得到：
[0097][0098]
进一步得到：
[0099][0100]
从而：
[0101][0102]
其中x
i
和y
i
分别表示p
i
和q
i
去中心化并跟随质心移动至自身所在坐标系的原点后的坐标；
[0103]
由于：
[0104][0105]
且由于和为常数，因此得到：
[0106][0107]
式中w是由w
i
组成的n
×
n对角阵，x和y分别是由x
i
和y
i
组成的3
×
n的矩阵；对xwy
t
做奇异值分解得到此时其中d＝v
t
ru；
[0108]
由于σ为奇异值构成的对角矩阵，d为正交矩阵，由正交矩阵性质得到：
[0109][0110]
步骤4
‑2‑
4：由式(3)，当d＝i时，tr(∑d)取得最大值，即求得最优的正交矩阵：
[0111][0112]
当的行列式为
‑
1时，该结果被排除，需要寻找次优解，此时最优旋转矩阵r表示为：
[0113][0114]
将式(4)代入t＝centroid
b
‑
r
·
centroid
a
即求得平移向量t；
[0115]
进一步地，所述步骤5具体如下：
[0116]
步骤5
‑
1：从数据集p
a
中选取m个点代入q
i
＝r
·
p
i
+t中，得到机器人基座标下的理论tcp点的坐标q
i
′
，使用公式(5)进行评价：
[0117][0118]
式中δ为tcp点坐标误差，γ表示孔坐标测量误差阈值；若误差δ大于阈值γ，则判定数据检测有误，重复步骤1到步骤4重新计算旋转矩阵r和平移向量t；若误差δ小于等于阈值γ，则判定基准孔坐标数据集p
a
、数据点集p
b
、旋转矩阵r和平移向量t有效；
[0119]
步骤5
‑
2：从数据集p
a
中取任意三个中心不共线的基准孔a、b、c，假设a、b、c三点的坐标分别为a(x
a
,y
a
,z
a
)、b(x
b
,y
b
,z
b
)、c(x
c
,y
c
,z
c
)，由于工件法向与基准孔所在平面垂直，利用a、b、c三个点组成的任意两个向量，求出基准孔所在平面的法向值
[0120]
已知半球形探头半径为r，基准孔内径为r；通过工件坐标系到机器人基坐标系的坐标转换方程计算出工件坐标系中任意点p在机器人基坐标系下对应的探头检测点p'的坐标，再通过式(6)计算实际对应于机器人基坐标系中p”的坐标：
[0121][0122]
其中d为工件基准孔中心测量坐标与实际坐标之间的固定偏差。
[0123]
具体实施例：
[0124]
参考附图2，本发明提供了一种人机协作装配中的机器人位姿标定方法，目的在于使用线面接触模式高效准确地建立工件坐标系与协作机器人基坐标系之间的关系，提高人机协作装配中协作机器人位姿标定效率。本实施例方法具体包括如下步骤：
[0125]
1、根据工件的基准孔特征选用合适的探针工具和标定工装，使用专用标定工装标定出探针的工具中心点(tcp)和工具坐标系姿态(tcf)。具体步骤如下：
[0126]
1.1：根据工件基准孔的大小选择大小合适的半球形末端探针和标定孔大小合适的标定工装，参考附图3，要求半球形探针前端可以伸入基准孔和标定工装孔一段距离，但半球形探头又不能完全伸入基准孔或标定工装孔内部，且工件基准孔与标定工装上的标定孔孔径大小一致；
[0127]
1.2：参考附图4，操作人员拖动机器人将探针的探头从四个差异明显的方向移向并紧紧贴合标定工装上的同一个标定孔，利用不同的机器人法兰位置坐标值可通过机器人控制器自动计算出探头球心tcp点坐标作为工具坐标系的原点；
[0128]
1.3：在标定杆件上标记加长杆轴线平行线，利用机器人控制器内置的2点世界坐标系法标定工具坐标系的x轴方向，从而标定工具坐标系姿态(tcf)，至此即可完成机器人的工具坐标系的标定。
[0129]
2、由操作人员从所建立的工件三维模型中提取基准点的坐标得到基准孔中心点坐标数据集p
a
(p1,p2,
…
,p
n
,n≥3)。具体步骤如下：
[0130]
2.1：参考附图5，建立工件的三维数学模型，并以其中一个基准孔的中心为原点建立工件坐标系；
[0131]
2.2：在步骤2.1建立的坐标系中，通过solidworks测量工具导出所有工件上基准孔的中心点坐标并选取其中的n个坐标构成基准点数据集p
a
。
[0132]
3、操作人员手动拖动引导机器人进行运动使得探针与步骤2中选取的基准点一一紧密接触，利用机器人的当前位姿和tcp标定结果计算出对应的工作空间中的点集p
b
。具体步骤如下：
[0133]
3.1：操作人员手动拖动机器人，使得标定探针的半球形探头完全与步骤2中选取的工件基准孔无缝贴合，此时记录当前机器人基坐标系下tcp点的坐标；
[0134]
3.2：重复步骤3.1直到记录完成所有步骤2中选取的工件基准孔对应的机器人末端tcp点坐标，构成数据点集p
b
。
[0135]
4、将第2步和第3步中的建立的基准点集p
a
和机器人计算出的工件对应点位的点集p
b
代入算法中，采用加权最小二乘法求解超定方程组的最优解，并利用奇异值分解求解工件三维模型中任意点的坐标到机器人基坐标系变换矩阵中的旋转矩阵r和平移向量t，之后检测数据有效性并最终确定工件坐标系与机器人基坐标系的转换关系，完成人机协作机
器人的位姿标定。具体步骤如下：
[0136]
4.1：参考附图6，分别对两组数据集p
a
和p
b
求解质心，并将数据集中的所有点跟随质心移动至原点。具体方法为：
[0137]
首先利用数据集质心求解公式求解数据集p
a
的质心centroid
a
和数据集p
b
的质心centroid
b
，其中n表示数据集中测量点的个数。之后进行去中心化处理，将数据集所有点跟随质心移动至原点。
[0138]
4.2：采用加权最小二乘法求解坐标转换方程组的最优解，并利用奇异值分解求解三维模型中任意点的坐标到机器人基坐标系变换矩阵中的旋转矩阵r和平移向量t。
[0139]
具体方法为：
[0140]
首先将满足条件的工件坐标系到机器人基座标系的转换矩阵中的旋转矩阵和平移向量分别记作(r,t)。任意一对数据集p
a
和数据集p
b
中的点(p
i
,q
i
)均满足q
i
＝r
·
p
i
+t，此超定方程组难以获得解析解，所以选择采用加权最小二乘法进行最优解的求取，并利用奇异值分解求解r、t。
[0141]
4.3：利用步骤4.2求得的机器人基坐标系与工件坐标系之间的转换关系，从基准点集p
a
中选取若干个点作为评价点，带入到坐标转换关系中，计算求得的理论工件坐标与机器人实测模型坐标之间的差异，并判断是否符合要求，若不符合要求则需要重新采集数据集并计算坐标系转换关系。具体原理为：
[0142]
从数据集p
a
中选取m个点代入到步骤4.2所求得到的转换关系q
i
＝r
·
p
i
+t中，得到机器人基座标下的理论工件坐标点q
i
'，使用公式(5)进行评价：
[0143][0144]
式(5)中q
i
表示实际测量得到的工件坐标点，γ表示孔坐标测量误差阈值。若计算所得误差δ超出阈值γ，则判定数据检测有误，需要重新采集并计算坐标系转换关系；若误差在可接受范围内，则认为数据有效。
[0145]
4.4：根据步骤4.2确定的机器人基坐标系与工件坐标系的转换关系和工件平面法向以及偏移距离d进一步精确工件坐标系与机器人基坐标系的转换关系。
[0146]
在实际标定过程中，利用半球形探针进行基准孔坐标检测时，所记录的坐标其实是tcp点坐标，但对于半球型探头，参考附图6，测量坐标与工件基准孔中心a的实际坐标之间会存在固定偏差d，又由于所测各孔具有相同尺寸，在这种情况下利用检测数据解算出的工件位姿是工件整体沿平面法向移动距离d后的位姿，因此需要根据步骤4.2确定的工件坐标系与机器人坐标系的转换关系和平面法向确定实际工件坐标系。
[0147]
首先从被评价为有效的数据集p
a
中取任意三个中心不共线的基准孔a,b,c，假设a,b,c三点的坐标分别为a(x
a
,y
a
,z
a
)，b(x
b
,y
b
,z
b
)，c(x
c
,y
c
,z
c
)，由于法向与基准孔所在平面垂直，利用a,b,c三个点组成的任意两个向量，即可求出平面的法向值
[0148]
之后参考附图6，已知半球形探头半径为基准孔内径为r；通过工件坐标系到机
器人基坐标系的坐标转换方程计算出工件上的任意点p在机器人基坐标系下对应的坐标p'，再通过式(6)计算经过补偿后工件上的任意点p在机器人基坐标系中的坐标p”：
[0149][0150]
其中d为工件基准孔中心测量坐标与实际坐标之间的固定偏差。