一种多人零和博弈可重构机器人最优控制方法及系统

1.本发明涉及机器人控制领域，特别是涉及一种多人零和博弈可重构机器人最优控制方法及系统。


背景技术：

2.可重构机器人是一类具有标准模块与接口，可根据不同的任务需求对自身构形进行重新组合与配置的机器人。根据“模块化”与“可重构”的设计理念，可重构机器人的每个关节模块均包含了通讯、传感、驱动、控制等单元，通过对这些模块进行重新配置可以使机器人呈现多种装配构形来完成不同的工作任务，从而表现出传统机器人所不具有的优势。在可重构机器人的使用过程中，交联耦合项是其固有的性质，由于其高度复杂非线性所以难以对其进行精确建模，这样就会影响可重构机器人控制的准确性、最优性以及稳定性。因此，处理可重构机器人系统的交联耦合项是十分必要的。
3.博弈理论关注了多参与者交互系统中的动态决策过程，根据最优控制的观点，一个完整的博弈理论包含了三个要素：参与者(控制器或智能体)、控制策略以及代价函数。根据参与者之间的关系，博弈可以分为合作博弈与非合作博弈。在非合作博弈中，理想的是所有参与者同时采取最优的策略来获得纳什均衡，其中任何一个参与者的结果不能通过单边改变来改善，零和博弈是完全非合作博弈。目前，并未有将零和博弈应用到可重构机器人系统的控制上，解决可重构机器人的控制问题。


技术实现要素：

4.本发明的目的是提供一种多人零和博弈可重构机器人最优控制方法及系统，以提高机器人系统的准确性和稳定性。
5.为实现上述目的，本发明提供了如下方案：
6.一种多人零和博弈可重构机器人最优控制方法，包括：
7.根据可重构机器人的转动惯量、加速比、摩擦力和所述可重构机器人子系统之间的交联耦合项构建子系统的动力学模型；
8.根据全局位置误差和所述动力学模型利用多人零和博弈方法构建性能指标函数；所述全局位置误差包括所述可重构机器人子系统的位置误差以及速度误差；
9.根据所述性能指标函数和所述动力学模型利用贝尔曼最优性原理得到哈密顿-雅克比-埃塞克方程；
10.通过所述哈密顿-雅克比-埃塞克方程和所述动力学模型确定补偿控制律；
11.利用神经网络对所述性能指标函数进行处理，得到近似权值；
12.利用所述近似权值和所述哈密顿-雅克比-埃塞克方程得到优化控制律；
13.根据所述补偿控制律和所述优化控制律确定所述可重构机器人的最优控制律。
14.可选地，所述根据全局位置误差和所述动力学模型利用多人零和博弈方法构建性能指标函数，具体包括：
15.根据所述动力学模型、可重构机器人子系统的位置分量及速度分量确定子系统的状态空间；
16.基于多人零和博弈方法利用漂移动力学对所述状态空间进行扩张，得到扩张函数；
17.根据所述扩张函数和所述全局位置误差构建性能指标函数。
18.可选地，所述根据所述性能指标函数和所述动力学模型利用贝尔曼最优性原理得到哈密顿-雅克比-埃塞克方程，具体包括：
19.将所述动力学模型进行转换，得到机器人速度动力学模型；
20.根据所述性能指标函数对所述机器人速度动力学模型进行最小化处理，得哈密顿函数；
21.根据所述哈密顿函数利用贝尔曼最优性原理得到哈密顿-雅克比-埃塞克方程。
22.可选地，所述通过所述哈密顿-雅克比-埃塞克方程和所述动力学模型确定补偿控制律，具体包括：
23.根据所述哈密顿-雅克比-埃塞克方程和可重构机器人子系统的鞍点确定子系统的第一控制律；
24.根据所述第一控制律和所述动力学模型中的子系统的设定模型确定补偿控制律。
25.可选地，所述利用所述近似权值和所述哈密顿-雅克比-埃塞克方程得到优化控制律，具体包括：
26.利用所述神经网络对所述性能指标函数的梯度进行处理，得到近似梯度；
27.根据所述近似权值和所述性能指标函数建立评判神经网络；
28.根据所述评判神经网络和所述第一控制律得到第二控制律；
29.根据所述第二控制律、所述哈密顿-雅克比-埃塞克方程、所述性能指标函数和所述近似梯度得到优化控制律。
30.可选地，所述根据所述补偿控制律和所述优化控制律确定所述可重构机器人的最优控制律，具体包括：
31.对所述补偿控制律和所述优化控制律进行求和，得到所述可重构机器人的最优控制律。
32.一种多人零和博弈可重构机器人最优控制系统，包括：
33.子系统的动力学模型构建模块，用于根据可重构机器人的转动惯量、加速比、摩擦力和所述可重构机器人子系统之间的交联耦合项构建子系统的动力学模型；
34.性能指标函数构建模块，用于根据全局位置误差和所述动力学模型利用多人零和博弈方法构建性能指标函数；所述全局位置误差包括所述可重构机器人子系统的位置误差以及速度误差；
35.哈密顿-雅克比-埃塞克方程构建模块，用于根据所述性能指标函数和所述动力学模型利用贝尔曼最优性原理得到哈密顿-雅克比-埃塞克方程；
36.补偿控制律确定模块，用于通过所述哈密顿-雅克比-埃塞克方程和所述动力学模型确定补偿控制律；
37.近似权值确定模块，用于利用神经网络对所述性能指标函数进行处理，得到近似权值；
38.优化控制律确定模块，用于利用所述近似权值和所述哈密顿-雅克比-埃塞克方程得到优化控制律；
39.最优控制律确定模块，用于根据所述补偿控制律和所述优化控制律确定所述可重构机器人的最优控制律。
40.可选地，所述性能指标函数构建模块，具体包括：
41.子系统的状态空间确定单元，用于根据所述动力学模型、可重构机器人子系统的位置分量及速度分量确定子系统的状态空间；
42.扩张单元，用于基于多人零和博弈方法利用漂移动力学对所述状态空间进行扩张，得到扩张函数；
43.性能指标函数构建单元，用于根据所述扩张函数和所述全局位置误差构建性能指标函数。
44.可选地，所述哈密顿-雅克比-埃塞克方程构建模块，具体包括：
45.转换单元，用于将所述动力学模型进行转换，得到机器人速度动力学模型；
46.最小化处理单元，用于根据所述性能指标函数对所述机器人速度动力学模型进行最小化处理，得哈密顿函数；
47.哈密顿-雅克比-埃塞克方程确定单元，用于根据所述哈密顿函数利用贝尔曼最优性原理得到哈密顿-雅克比-埃塞克方程。
48.可选地，所述补偿控制律确定模块，具体包括：
49.第一控制律确定单元，用于根据所述哈密顿-雅克比-埃塞克方程和可重构机器人子系统的鞍点确定子系统的第一控制律；
50.补偿控制律确定单元，用于根据所述第一控制律和所述动力学模型中的子系统的设定模型确定补偿控制律。
51.根据本发明提供的具体实施例，本发明公开了以下技术效果：
52.本发明提供的多人零和博弈可重构机器人最优控制方法和系统，根据可重构机器人的转动惯量、加速比、摩擦力和可重构机器人子系统之间的交联耦合项构建子系统的动力学模型；根据全局位置误差和动力学模型利用多人零和博弈方法构建性能指标函数；根据性能指标函数和动力学模型利用贝尔曼最优性原理得到哈密顿-雅克比-埃塞克方程；通过哈密顿-雅克比-埃塞克方程和动力学模型确定补偿控制律；利用神经网络对性能指标函数进行处理，得到近似权值；利用近似权值和哈密顿-雅克比-埃塞克方程得到优化控制律；根据补偿控制律和优化控制律确定可重构机器人的最优控制律。在位置跟踪方面，采用了多人零和博弈消除了交联耦合项的影响，改善了因为存在交联耦合项的可重构机器人系统跟踪性能低的情况，加快系统的跟踪速度，并且使关节位置的稳态误差减小，从而提高机器人系统的准确性和稳定性。
附图说明
53.为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动性的前提下，还可以根据这些附图获得其他的附图。
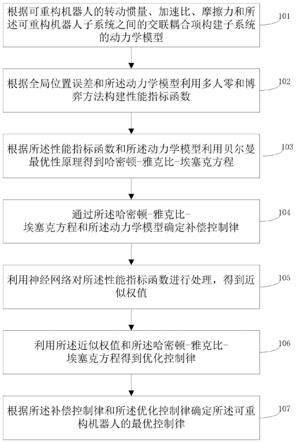
54.图1为本发明提供的多人零和博弈可重构机器人最优控制方法流程图；
55.图2为本发明提供的多人零和博弈可重构机器人最优控制方法简化流程图；
56.图3为本发明提供的多人零和博弈可重构机器人最优控制系统示意图。
具体实施方式
57.下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。
58.本发明的目的是提供一种多人零和博弈可重构机器人最优控制方法及系统，以提高机器人系统的准确性和稳定性。
59.为使本发明的上述目的、特征和优点能够更加明显易懂，下面结合附图和具体实施方式对本发明作进一步详细的说明。
60.如图1所示，本发明提供的多人零和博弈可重构机器人最优控制方法，包括：
61.步骤101：根据可重构机器人的转动惯量、加速比、摩擦力和所述可重构机器人子系统之间的交联耦合项构建子系统的动力学模型。
62.步骤102：根据全局位置误差和所述动力学模型利用多人零和博弈方法构建性能指标函数；所述全局位置误差包括所述可重构机器人子系统的位置误差以及速度误差。
63.步骤103：根据所述性能指标函数和所述动力学模型利用贝尔曼最优性原理得到哈密顿-雅克比-埃塞克方程。
64.步骤104：通过所述哈密顿-雅克比-埃塞克方程和所述动力学模型确定补偿控制律。
65.步骤105：利用神经网络对所述性能指标函数进行处理，得到近似权值。
66.步骤106：利用所述近似权值和所述哈密顿-雅克比-埃塞克方程得到优化控制律。
67.步骤107：根据所述补偿控制律和所述优化控制律确定所述可重构机器人的最优控制律。
68.其中，所述步骤102根据全局位置误差和所述动力学模型利用多人零和博弈方法构建性能指标函数，具体包括：
69.根据所述动力学模型、可重构机器人子系统的位置分量及速度分量确定子系统的状态空间。
70.基于多人零和博弈方法利用漂移动力学对所述状态空间进行扩张，得到扩张函数。
71.根据所述扩张函数和所述全局位置误差构建性能指标函数。
72.其中，所述步骤103根据所述性能指标函数和所述动力学模型利用贝尔曼最优性原理得到哈密顿-雅克比-埃塞克方程，具体包括：
73.将所述动力学模型进行转换，得到机器人速度动力学模型。
74.根据所述性能指标函数对所述机器人速度动力学模型进行最小化处理，得哈密顿函数。
75.根据所述哈密顿函数利用贝尔曼最优性原理得到哈密顿-雅克比-埃塞克方程。
76.其中，所述步骤104通过所述哈密顿-雅克比-埃塞克方程和所述动力学模型确定补偿控制律，具体包括：
77.根据所述哈密顿-雅克比-埃塞克方程和可重构机器人子系统的鞍点确定子系统的第一控制律。
78.根据所述第一控制律和所述动力学模型中的子系统的设定模型确定补偿控制律。
79.其中，所述步骤106利用所述近似权值和所述哈密顿-雅克比-埃塞克方程得到优化控制律，具体包括：
80.利用所述神经网络对所述性能指标函数的梯度进行处理，得到近似梯度。
81.根据所述近似权值和所述性能指标函数建立评判神经网络。
82.根据所述评判神经网络和所述第一控制律得到第二控制律。
83.根据所述第二控制律、所述哈密顿-雅克比-埃塞克方程、所述性能指标函数和所述近似梯度得到优化控制律。
84.其中，所述步骤107根据所述补偿控制律和所述优化控制律确定所述可重构机器人的最优控制律，具体包括：
85.对所述补偿控制律和所述优化控制律进行求和，得到所述可重构机器人的最优控制律。
86.本发明还提供一种多人零和博弈可重构机器人最优控制方法在实际应用中的具体方式，如图2所示，具体过程如下：
87.该方法首先建立可重构机器人系统的动力学模型，其次构建多人零和博弈的性能指标函数，接下来求解哈密顿-雅克比-埃塞克方程，最后通过实验验证所提出控制方法的有效性。
88.1、可重构机器人动力学模型建立
89.建立可重构机器人第i个子系统的动力学模型：
[0090][0091]
其中，i
mi
为电机的转动惯量，γi为子系统的减速比，是第i个子系统的位置、速度以及加速度，为摩擦力矩项，为子系统之间的交联耦合项，τ
si
为与传感器有关的耦合力矩，τi为控制输出力矩。为整体机器人系统的位置、速度、加速度向量。
[0092]
由于摩擦力矩项是与关节位置和速度有关的函数，因此可以具体表示为：
[0093][0094]
其中，f
bi
,f
si
,f
τi
,f
ci
分别为第i个子系统的滑动摩擦、静摩擦、库伦摩擦以及边界摩擦；为建模摩擦误差，基于线性化方法，公式(2)可以近似表示为：
[0095][0096]
其中，分别为第i个子系统的滑动摩擦、静摩擦、库伦摩擦以及边界摩擦
的估计值，为不确定摩擦系数，为速度误差矩阵。
[0097]
子系统之间的交联耦合项是一个复杂的高度非线性复杂函数，表示为：
[0098][0099]
其中，z
mi
,z
lj
和z
lk
是沿着第i个电机、第j个连杆以及第k个连杆轴旋转的单位向量，为了方便表示，定义常数向量以及改写公式(4)，可以得到：
[0100][0101]
其中，u
zi
,v
zi
分别为交联耦合项的常分量以及变分量，表示z
mi
与z
lj
的点乘积，表示常分量建模误差，表示z
mi
与z
lk
×zlj
的点乘积，表示变分量建模误差。
[0102]
将公式(1)表示成与机器人速度有关的形式：
[0103][0104]
其中，公式(6)为机器人速度动力学模型。控制输入矩阵定义为bi＝(i
mi
γi)-1
，定义系统的状态其中x
i1
，x
i2
分别为第i个子系统的位置以及速度分量，定义控制输入向量为ui，因此公式(1)可以转换为第i个子系统的状态空间：
[0105][0106]
其中，为可以精确测量的系统模型即系统漂移动力学模型，为全局模型不确定性，yi表示系统的输出。
[0107]
为了建立多人零和博弈的性能指标以及求解哈密顿-雅克比-埃塞克方程，将上述函数扩张为矩阵的形式，f(x)＝[f1(x1),...,fi(xi),...,fn(xn)]
t
为漂移动力学，gi(xi)＝[0,
…
,bi,
…
,0]
t
为控制输入，hj＝[0,
…
,hj(x),
…
,0]
t
是模型不确定性，基于多人零和博弈框架，公式(7)可以改写为：
[0108]
[0109]
其中，x是全局机器人向量，为全局机器人的状态。
[0110]
2、多人零和博弈的性能指标函数建立
[0111]
首先，构建性能指标函数为：
[0112][0113]
其中，全局位置误差为e＝[e1,
…
,ei,
…
,en]
t
,ei＝x
i1-x
id
，为第i个子系统的位置以及速度误差；为期望位置、速度和及速度，q,ri,sj是正定矩阵，ui＝[0,
…
,ui,
…
,0]
t
为扩张控制输入，为效用函数。对公式(6)进行最小化可以得到哈密顿函数：
[0114][0115]
其中，表示期望的全局加速度，为的偏导数，为的最优值。根据贝尔曼最优性原理，可以得到哈密顿-雅克比-埃塞克方程为：
[0116][0117]
为了求得系统的鞍点可以通过两个固定条件求得：
[0118][0119]
根据(11)和(12)，系统的最优控制律和最坏模型不确定项为：
[0120][0121][0122]
公式(13)表示最优控制律为第一控制律，此时，不是最终要得到的最优控制律。t表示转置，ri为第i个子系统的正定控制矩阵。
[0123]
将(13)和(14)代入(10)，可以得到系统的哈密顿-雅克比-埃塞克方程为：
[0124][0125]
改写最优控制律(13)为：
[0126][0127]
其中，补偿控制律u
i1
去处理模型确定性fi(xi)，优化控制律去补偿模型不确定性hj(x)。因为x
id
和ei是已知的，根据公式(7)中的fi(xi)表达式，可确定补偿控制律u
i1
：
[0128][0129]
3、哈密顿-雅克比-埃塞克方程的求解
[0130]
利用神经网络来近似性能指标函数其中，神经网络为三层前向神经网络，定义如下：
[0131][0132]
其中，wc是理想的权值向量，是激活函数，εc是神经网络的逼近误差，的梯度通过神经网络近似为：
[0133][0134]
其中：和分别为激活函数的梯度和逼近误差。
[0135]
由于理想权值向量wc是未知的，所以用近似权值建立一个评判神经网络来估计性能指标函数：
[0136][0137]
根据哈密顿方程(10)和性能指标函数(18)以及它的梯度(19)，哈密顿方程可以进一步改写为：
[0138][0139]
其中，为ui,hj的估计值。
[0140]
将(20)代入(13)和(14)，可以得到
[0141][0142][0143]
将(22)、(23)代入(10)，可以得到
[0144][0145]
令函数误差ec被评判神经网络所调节，可得
[0146][0147]
根据梯度下降法可以得到权值更新律为
[0148][0149]
优化控制律是通过权值更新律进行更新的。
[0150]
结合(17)和(22)，可以得到基于多人零和博弈的可重构机器人最优控制律：
[0151][0152]
4、实验验证
[0153]
为了验证所提出的基于多人零和博弈的可重构机器人最优控制律方法的有效性，建立一个二自由度可重构机器人模型进行实验验证，其中包括增量式编码器、直流电机、谐
波减速器、绝对式编码器以及关节力矩传感器。直流电机的型号是maxon公司的218014、额定电压为48v、额定力矩为190mnm、减速比为100:1。电机侧的位置变量是由maxon公司的500线增量式编码器测量的，连杆侧的位置变量是由netzer公司的19位编码器测量的。关节力矩传感器的额定力矩为20nm被嵌在关节模块末端。采用quanser公司生产的线性功率放大器驱动关节模块的电动机和qpide数据采集卡采集各传感器的数据。
[0154]
通过实验结果表明，所提出的基于多人零和博弈的可重构机器人最优控制律方法为可重构机器人提供稳定性和精确性，以满足各种任务的要求。
[0155]
如图3所示，本发明提供的一种多人零和博弈可重构机器人最优控制系统，包括：
[0156]
子系统的动力学模型构建模块301，用于根据可重构机器人的转动惯量、加速比、摩擦力和所述可重构机器人子系统之间的交联耦合项构建子系统的动力学模型。
[0157]
性能指标函数构建模块302，用于根据全局位置误差和所述动力学模型利用多人零和博弈方法构建性能指标函数；所述全局位置误差包括所述可重构机器人子系统的位置误差以及速度误差。
[0158]
哈密顿-雅克比-埃塞克方程构建模块303，用于根据所述性能指标函数和所述动力学模型利用贝尔曼最优性原理得到哈密顿-雅克比-埃塞克方程。
[0159]
补偿控制律确定模块304，用于通过所述哈密顿-雅克比-埃塞克方程和所述动力学模型确定补偿控制律。
[0160]
近似权值确定模块305，用于利用神经网络对所述性能指标函数进行处理，得到近似权值。
[0161]
优化控制律确定模块306，用于利用所述近似权值和所述哈密顿-雅克比-埃塞克方程得到优化控制律。
[0162]
最优控制律确定模块307，用于根据所述补偿控制律和所述优化控制律确定所述可重构机器人的最优控制律。
[0163]
其中，所述性能指标函数构建模块，具体包括：
[0164]
子系统的状态空间确定单元，用于根据所述动力学模型、可重构机器人子系统的位置分量及速度分量确定子系统的状态空间。
[0165]
扩张单元，用于基于多人零和博弈方法利用漂移动力学对所述状态空间进行扩张，得到扩张函数。
[0166]
性能指标函数构建单元，用于根据所述扩张函数和所述全局位置误差构建性能指标函数。
[0167]
其中，所述哈密顿-雅克比-埃塞克方程构建模块，具体包括：
[0168]
转换单元，用于将所述动力学模型进行转换，得到机器人速度动力学模型。
[0169]
最小化处理单元，用于根据所述性能指标函数对所述机器人速度动力学模型进行最小化处理，得哈密顿函数。
[0170]
哈密顿-雅克比-埃塞克方程确定单元，用于根据所述哈密顿函数利用贝尔曼最优性原理得到哈密顿-雅克比-埃塞克方程。
[0171]
其中，所述补偿控制律确定模块，具体包括：
[0172]
第一控制律确定单元，用于根据所述哈密顿-雅克比-埃塞克方程和可重构机器人子系统的鞍点确定子系统的第一控制律。
[0173]
补偿控制律确定单元，用于根据所述第一控制律和所述动力学模型中的子系统的设定模型确定补偿控制律。
[0174]
本发明首先建立可重构机器人系统的动力学模型，其次构建性能指标函数与哈密顿-雅克比-埃塞克方程，通过神经网络近似性能指标函数来求哈密顿-雅克比-埃塞克方程的解，最后通过实验验证所提出控制方法的有效性。借助了零和博弈的这种观点，把可重构机器人系统的控制器与其交联耦合项分别作为博弈系统的两个参与者进行博弈，能够使机器人系统达到准确性、最优性以及稳定性。解决了现有技术中对于存在交联耦合项的系统不能保证准确性、最优性以及稳定性的问题，并且可以满足各种任务的需求。
[0175]
在位置跟踪方面，本发明改善了因为存在交联耦合项的可重构机器人系统跟踪性能低的情况，并且采用了多人零和博弈消除了交联耦合项的影响，加快系统的跟踪速度，并且使关节位置的稳态误差减小。
[0176]
在控制力矩方面，本发明的控制力矩更加连续和平滑，不仅可以保持系统渐进稳定，而且可以降低每个关节的能量损耗。
[0177]
本说明书中各个实施例采用递进的方式描述，每个实施例重点说明的都是与其他实施例的不同之处，各个实施例之间相同相似部分互相参见即可。对于实施例公开的系统而言，由于其与实施例公开的方法相对应，所以描述的比较简单，相关之处参见方法部分说明即可。
[0178]
本文中应用了具体个例对本发明的原理及实施方式进行了阐述，以上实施例的说明只是用于帮助理解本发明的方法及其核心思想；同时，对于本领域的一般技术人员，依据本发明的思想，在具体实施方式及应用范围上均会有改变之处。综上所述，本说明书内容不应理解为对本发明的限制。