一种基于阻尼最小二乘的多关节机械臂避障逆运动学方法

1.本发明属于机械臂运动学领域的一种多关节机械臂的逆运动学方法，具体涉及了一种基于阻尼最小二乘的多关节机械臂避障逆运动学方法。


背景技术：

2.多关节机械臂是冗余机械臂的一种，在三个位置自由度和三个姿态自由度以外还拥有较多冗余自由度，这导致了多关节机械臂自运动的特性，也就是在保证末端位姿固定的情况下，各关节仍然可以运动。因此，这类机械臂的运动灵活性很高，可以在末端位姿不变的同时完成避障，十分适合在复杂环境下作业。
3.多关节机械臂的避障的首要步骤就是逆运动学的求解，由于自由度的极大冗余，多关节机械臂的逆运动学解析解往往不存在，即使存在解析解也往往伴随了难以筛选的多个解，考虑到多关节机械臂逆运动学的复杂性，目前常见的逆运动学求解方法一般不考虑障碍约束。


技术实现要素：

4.为了克服多关节机械臂冗余自由度带来的困难，在避障需求下充分利用多关节机械臂的灵活性，为提高具有冗余自由度的多关节机械臂在复杂环境下的作业性能，本发明提供了一种基于阻尼最小二乘的多关节机械臂避障逆运动学方法。本发明针对多关节机械臂在运动过程中实时避障问题，给定机械臂的末端位姿、障碍物空间坐标和障碍物大小，基于阻尼最小二乘方法设计了机械臂的逆运动学优化函数，采用迭代求解得到最终满足避障条件的关节角度，简化了多关节机械臂避障的方法复杂度。
5.为实现上述目的，本发明的技术方案具体内容如下：
6.本发明包括以下步骤：
7.第一步：根据多关节机械臂的结构建立d-h关节坐标系，基于d-h关节坐标系求出多关节机械臂的正运动学的坐标转换关系和雅可比矩阵；
8.第二步：根据障碍物与多关节机械臂中各连杆之间的相对位置关系以及多关节机械臂的正运动学的坐标转换关系，计算障碍物对多关节机械臂中各连杆的总虚拟斥力；
9.第三步：基于阻尼最小二乘法，根据雅可比矩阵和虚拟斥力建立多关节机械臂逆运动学优化目标函数，采用数值迭代方法求解多关节机械臂逆运动学优化函数，获得多关节机械臂的末端位姿对应的各关节角度。
10.所述第二步具体为：
11.2.1)根据障碍物与多关节机械臂中连杆之间的相对位置关系以及多关节机械臂的正运动学的坐标转换关系，计算各个障碍物对多关节机械臂中每一连杆的虚拟斥力的作用方向以及对应虚拟斥力势能；
12.2.2)将各个障碍物对多关节机械臂中当前连杆的虚拟斥力的作用方向和对应虚拟斥力势能相乘后，获得各个障碍物对多关节机械臂中当前连杆的虚拟斥力，接着对各个
虚拟斥力进行求和，获得障碍物对多关节机械臂中当前连杆的总虚拟斥力；
13.2.3)重复2.1)-2.2)，计算并获得障碍物对多关节机械臂中剩余连杆的总虚拟斥力。
14.所述各个障碍物对多关节机械臂中每一连杆的虚拟斥力的作用方向由障碍物与连杆之间的相对位置确定，具体地：
15.针对障碍物k对连杆i的虚拟斥力的作用方向，障碍物k的几何中心o与连杆i的两个端点pa、pb之间的距离opa、opb以及连杆i的两个端点pa、pb相连后构成轴线papb之间的关系分为以下三种情况：
16.当障碍物k的几何中心o在连杆i的轴线papb上的投影位于pb一侧的延长线上时，障碍物k到连杆i的空间距离d
ik
满足d
ik
＝|opb|-r-rk，r为连杆i端部所在圆的半径，rk为障碍物的最大直径的一半，虚拟斥力的作用方向为
17.当障碍物k的几何中心o在连杆i的轴线papb上的投影位于pa一侧的延长线上时，障碍物k到连杆i的空间距离d
ik
满足d
ik
＝|opa|-r-rk，虚拟斥力的作用方向为
18.当障碍物k的几何中心o在连杆i的轴线papb上的投影位于轴线papb之间时，障碍物k到连杆i的空间距离d
ik
满足d
ik
＝|opv|-r-rk，虚拟斥力的作用方向为
19.所述各个障碍物对多关节机械臂中当前连杆的虚拟斥力势能的计算公式如下：
[0020][0021]
式中，e
ik
表示障碍物k作用于连杆i的虚拟斥力势能，kr为障碍物斥力系数，d0为障碍物的影响距离，d
ik
为障碍物k到连杆i的空间距离；
[0022]
所述第三步中，多关节机械臂逆运动学优化目标函数的公式为：
[0023][0024]
其中，j是多关节机械臂的雅可比矩阵，f
force
(q)表示虚拟斥力对关节的累计作用力，f
force
(q)是虚拟斥力对连杆的作用分量，q表示多关节机械臂的各关节角度，λ2表示正则项系数，x表示多关节机械臂的末端位置，‖‖表示取二范数操作，min表示取最小值操作，γ是与迭代次数p有关的斥力衰退系数。
[0025]
所述第三步的采用数值迭代法求解逆运动学优化目标函数的求解过程中，通过调整各关节角度q获得更新的末端位姿根据更新的末端位姿与预设末端位姿0te计算位姿残差，使位姿残差最小后，获得最终的各关节角度q，求解过程中的公式如下：
[0026][0027]hp
＝(j
ptjp
+λ2i)-1
[0028]
γ＝σ
p
[0029][0030]
其中，h
p
是第p次迭代时的hessian矩阵，j
p
是第p次迭代时的雅可比矩阵，e
p
是第p次迭代时的位姿残差，λ2是正则项系数，tr()表示将齐次矩阵转换为向量形式的操作，γ是
与迭代次数p有关的斥力衰退系数；表示正运动学关系，σ是单步斥力衰退系数，t表示转置操作，q
p
、q
p+1
分别表示第p、p+1次迭代时的各关节角度。
[0031]
所述多关节机械臂的相邻连杆之间采用万向节进行连接。
[0032]
与现有技术相比，本发明的有益效果是：
[0033]
1.提出了一种多关节机械臂的逆运动学方法，能够在已知机械臂基础信息(关节个数，各关节长度等信息)和障碍物信息(空间位置、大小)的情况下，得到满足避障条件的机械臂关节角度组合，充分利用了多关节机械臂的冗余自由度以满足避障作业的需求。
[0034]
2.综合考虑了多种障碍物与机械臂连杆的相对位置情况，提出了基于势能的虚拟斥力表达式，定义了具有明确物理意义的虚拟斥力表达式，保障了有障碍物情况下多关节机械臂作业的安全性。
[0035]
3.使用数值迭代方法求解考虑了虚拟斥力的阻尼最小二乘方程，在方程没有解析解的情况下仍满足了逆运动学求解的精确性和实时性。
附图说明
[0036]
图1是多关节机械臂的外观示意图；
[0037]
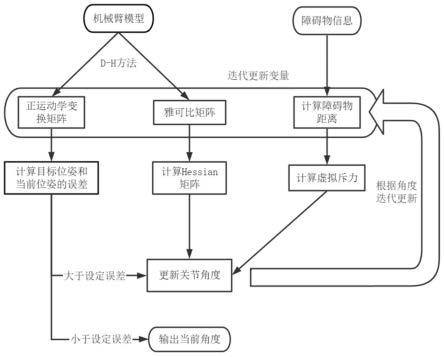
图2是方法步骤流程图；
[0038]
图3是坐标系定义示意图；
[0039]
图4是障碍物距离计算示意图；
[0040]
图5是本发明在matlab中演示的多关节机械臂避障过程图；
[0041]
图6是本发明在matlab仿真实验中的多关节机械臂末端位姿误差结果图。
具体实施方式
[0042]
下面结合实例与附图对本发明的求解过程做更详细的描述。
[0043]
本实施例中，多关节机械臂的连杆序号为i＝1,2,
…
,i，从基座向外依次排序，总数量为i，每节连杆呈圆柱体形状，长度为l，半径为r，连杆之间采用万向节连接，如图1所示。
[0044]
对于机械臂第i个连杆处的万向节，采用两个相互垂直的旋转角度θi、对万向节的两个旋转自由度进行描述，对于万向节中心处的坐标系{o-xyz}来说，绕z轴的旋转角度为θi，绕y轴的旋转角度为如图3所示，则可以将关节角度定义为
[0045]
如图2所示，本发明包括以下步骤：
[0046]
第一步：根据多关节机械臂的结构建立d-h关节坐标系，基于d-h关节坐标系求出多关节机械臂的正运动学的坐标转换关系和雅可比矩阵；
[0047]
具体实施中，在万向节中心建立d-h坐标系{o
n-x
nynzn
}，n＝1,2,
…
,n表示转动自由度的序号，n＝2i，即每个万向节存在两个垂直方向的转动自由度，万向节处的坐标定义如图3所示。
[0048]
机械臂的正运动学通常可以表示为如下函数形式：
[0049][0050]
它表明末端执行器的位姿ξe是关于关节角度q的一个函数。根据d-h法，采用齐次
变换，其表达式将是由单个连杆变换矩阵的简单乘积，可以得到正运动学的坐标转换关系为：
[0051]
ξe～0te＝0a1·1a2…
n-1an
[0052]
其中，是4
×
4的齐次矩阵，由旋转矩阵r3×3和平移向量t3×1组成，
n-1an
是d-h坐标系间的转换矩阵，可表示为：
[0053][0054]
其中qn,αn,an,dn为d-h法中描述机械臂连杆的参数。
[0055]
同时，为方便后续逆运动学分析，还需要求出机械臂的雅可比矩阵，它的形式为：
[0056][0057]
雅可比矩阵可以通过对机械臂的正运动学的公式求导得到。
[0058]
第二步：根据障碍物与多关节机械臂中各连杆之间的相对位置关系以及多关节机械臂的正运动学的坐标转换关系，计算障碍物对多关节机械臂中各连杆的总虚拟斥力；
[0059]
第二步具体为：
[0060]
2.1)根据障碍物与多关节机械臂中连杆之间的相对位置关系以及多关节机械臂的正运动学的坐标转换关系，计算各个障碍物对多关节机械臂中每一连杆的虚拟斥力的作用方向以及对应虚拟斥力势能；
[0061]
各个障碍物对多关节机械臂中每一连杆的虚拟斥力的作用方向由障碍物与连杆之间的相对位置确定，具体地：
[0062]
针对障碍物k对连杆i的虚拟斥力的作用方向，如图4所示，障碍物k的几何中心o与连杆i的两个端点pa、pb之间的距离opa、opb以及连杆i的两个端点pa、pb相连后构成轴线papb之间的关系分为以下三种情况，其中，连杆i的前后端点的位置pa、pb可以通过计算d-h坐标系间的转换矩阵，由正运动学的坐标转换关系求得：
[0063]
如图4的(a)所示，当障碍物k的几何中心o在连杆i的轴线papb上的投影位于pb一侧的延长线上时，即|opb|2+|papb|2≤|opa|2，障碍物k到连杆i的空间距离d
ik
满足d
ik
＝|opb|-r-rk，r为连杆i端部所在圆的半径，rk为障碍物的最大直径的一半，虚拟斥力的作用方向为对应的虚拟斥力ef满足
[0064]
如图4的(b)所示，当障碍物k的几何中心o在连杆i的轴线papb上的投影位于pa一侧
的延长线上时，即|opa|2+|papb|2≤|opb|2，障碍物k到连杆i的空间距离d
ik
满足d
ik
＝|opa|-r-rk，虚拟斥力的作用方向为对应的虚拟斥力ef满足
[0065]
如图4的(c)所示，当障碍物k的几何中心o在连杆i的轴线papb上的投影位于轴线papb之间时，障碍物k到连杆i的空间距离d
ik
满足d
ik
＝|opv|-r-rk，虚拟斥力的作用方向为对应的虚拟斥力ef满足
[0066]
各个障碍物对多关节机械臂中当前连杆的虚拟斥力势能的计算公式如下：
[0067][0068]
式中，e
ik
表示障碍物k作用于连杆i的虚拟斥力势能，kr为障碍物斥力系数，d0为障碍物的影响距离，d
ik
为障碍物k到连杆i的空间距离；在具体实施中，假设障碍物设置在包围球中，障碍物的几何中心位置为包围球的球心，障碍物的最大直径为包围球的直径，包围球的半径为rk，连杆为圆柱形，即d
ik
表示圆柱体连杆与包围球的空间距离。
[0069]
2.2)将各个障碍物对多关节机械臂中当前连杆的虚拟斥力的作用方向和对应虚拟斥力势能相乘后，获得各个障碍物对多关节机械臂中当前连杆的虚拟斥力，接着对各个虚拟斥力进行求和，获得障碍物对多关节机械臂中当前连杆的总虚拟斥力；
[0070]
具体实施中，将所有虚拟斥力进行矢量相加，随后通过坐标转换将虚拟斥力转换到各个关节坐标系下，0rb为点pb在基座坐标系下的旋转矩阵，可以由正运动学的坐标转换关系求得点pb的转换矩阵tb并分解后得到，至此，可以得到空间中障碍物对连杆i的总虚拟斥力ei为：
[0071]ei
＝0r
b-1
·
∑e
ik
[0072]
每一个连杆i的姿态由θi、两个关节角度控制，因此作用于θi、的关节斥力分别为ei在y轴和z轴的分量，因此连杆i的关节斥力组成向量为：
[0073][0074]
2.3)重复2.1)-2.2)，计算并获得障碍物对多关节机械臂中剩余连杆的总虚拟斥力。
[0075]
机械臂逆运动学求解是给定末端位姿矩阵ξe，得到关节角的过程，表示为：
[0076][0077]
第三步中，在阻尼最小二乘法的基础上，考虑虚拟斥力对关节的影响，多关节机械臂逆运动学优化目标函数的公式为：
[0078][0079]
其中，j是多关节机械臂的雅可比矩阵，f
force
(q)表示虚拟斥力对关节的累计作用力，f
force
(q)是虚拟斥力对连杆的作用分量，q表示多关节机械臂
的各关节角度，λ2表示正则项系数，本实施例中取这可以使最终位姿误差更小，x表示机械臂的末端位置，‖‖表示取二范数操作，min表示取最小值操作，γ是用于迭代求解的斥力衰退系数，与迭代次数p有关，在迭代过程中逐渐减小，具体形式见下文。优化目标函数的公式表明要在机械臂末端跟踪轨迹误差最小和关节速度范数最小的同时，尽量减少斥力的影响，对于多关节机械臂来说，这可以使逆运动学求解得到的多关节机械臂位姿更加远离障碍物和关节极限位置。
[0080]
第三步的采用数值迭代法求解逆运动学优化目标函数的求解过程中，通过调整各关节角度q获得更新的末端位姿，其中t表示转置操作，使得更新的末端位姿不断逼近预设末端位姿，根据更新的末端位姿与预设末端位姿0te计算位姿残差，迭代中使位姿残差最小后，具体实施中，位姿残差小于预设阈值后，即位姿残差最小，停止迭代，获得最终的各关节角度q，求解过程中的公式如下：
[0081][0082]hp
＝(j
ptjp
+λ2i)-1
[0083]
γ＝σ
p
[0084][0085]
其中，h
p
是第p次迭代时的hessian矩阵，j
p
是第p次迭代时的雅可比矩阵，e
p
是第p次迭代时的位姿残差，满足e
p
＝[dv
x
,dvy,dvz,dω
x
,dω
x
,dωz]
t
，dv
x
、dvy、dvz分别表示x、y、z轴上的位置残差，dω
x
、dω
x
、dωz分别表示x、y、z轴上的角度残差，λ2是正则项系数，tr()表示将齐次矩阵转换为向量形式的操作，γ是与迭代次数p有关的斥力衰退系数，它随着迭代次数减小，σ是单步斥力衰退系数，一个常数，σ∈(0,1)，本实施例中取σ＝0.5；表示正运动学关系，t表示转置操作，q
p
、q
p+1
分别表示第p、p+1次迭代时的各关节角度。
[0086]
开始的几次迭代，f
force
(q)引导关节快速的远离障碍物或关节极限位置，避免局部最小值的影响，在迭代后期，f
force
(q)的系数γ趋近于0，使迭代更快速地向目标位姿收敛，保证了改进算法的收敛性。
[0087]
本发明的matlab仿真避障过程图如图5的(a)-(d)所示，可以看到，多关节机械臂在障碍物移动的情况下成功避障，并可以跟随期望的末端位姿。如图6的(a)和(b)所示，实际与期望末端位置的误差小于10-10
米，实际与期望末端角度的误差小于10-10
rad，满足了逆运动学求解的精确性。