基于控制障碍函数的模型不确定机器人安全控制方法

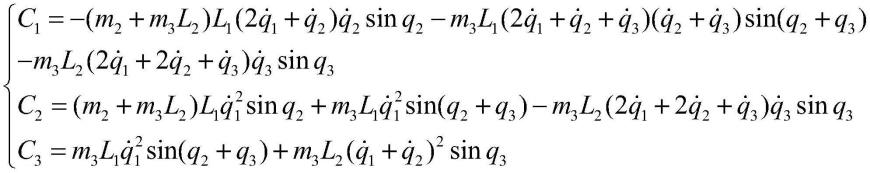
1.本发明涉及基于控制障碍函数的模型不确定机器人安全控制方法，属于机器人控制技术领域，特别涉及一种机器人动力学模型不确定情况下，基于控制障碍函数实现安全控制的方法。


背景技术：

2.在当前机器人技术领域，安全性作为机器人与环境交互过程中最重要的性能之一，受到越来越多的关注。为了满足安全性要求，设计控制器时需要考虑安全约束条件，如轨迹跟踪过程中对障碍物的躲避，人机交互时限制接触力以保障人体安全等。目前常用的控制设计方法包括模型预测控制，人工势场方法等。此外，基于控制障碍函数的安全控制方法近来得到快速发展，其相较于模型预测控制具有更高的运算效率，相较于人工势场方法具有更小的保守性。
3.上述控制方法均依赖于机器人的精确动力学模型，但机器人是一个强耦合，非线性系统，甚至存在干扰问题，导致很难建立精确的模型。因此，上述方法设计的控制器安全效果无法得到保障。


技术实现要素：

4.本发明的技术解决问题是：克服已有安全控制方法存在的不足，提出基于控制障碍函数的模型不确定机器人安全控制方法，该方法将轨迹规划和轨迹跟踪任务相结合，在机器人动力学模型不精确的情况下，通过高斯过程回归估计模型不确定部分，从而基于控制障碍函数完成安全控制器的设计，全程保证任务的安全性。
5.本发明的技术解决方案是：
6.基于控制障碍函数的模型不确定机器人安全控制方法，该方法的步骤包括：
7.第一步，建立机器人动力学估计模型；
8.第二步，获得满足安全约束的机器人关节速度，并对机器人关节速度进行数值积分，获得安全的机器人关节位置；
9.第三步，跟踪第二步获得的安全的机器人关节位置，得到跟踪过程中的机器人关节速度、机器人关节加速度和机器人关节力矩；
10.第四步，跟踪第一步建立的机器人动力学估计模型，得到跟踪过程中的模型关节加速度；
11.第五步，求取第三步得到的机器人关节加速度与第四步得到的模型关节加速度的差值，得到模型误差数据；
12.第六步，根据第三步得到的机器人关节速度、机器人关节加速度和机器人关节力矩以及第五步得到的模型误差数据进行高斯过程回归，得到机器人动力学精确模型；
13.第七步，根据第六步得到的机器人动力学精确模型，得到满足安全约束的控制指令，并将获得的满足安全约束的控制指令对机器人进行安全控制，完成基于控制障碍函数
的模型不确定机器人安全控制。
14.所述的第一步中，建立的机器人动力学估计模型为：
[0015][0016]
其中，表示n个关节的位置，是机器人的惯性矩阵，表示离心力与科氏力矩阵，表示重力项，表示重力项，分别为m(q)，g(q)的估计值，为模型误差；u为控制输入。
[0017]
所述的第二步中，采用二次规划模型获得满足安全约束的机器人关节速度。
[0018]
所述的二次规划模型为：
[0019][0020][0021]qmin
≤q≤q
max
[0022]
其中，表示满足安全约束的机器人关节速度，q表示当前机器人关节位置；表示当前机器人关节速度，表示期望关节速度，e＝x(q)-xd(t)表示机器人末端位置跟踪误差，t表示当前时间，γ》0，γ为一常数，是一设定值，表示伪逆矩阵；x(q)为当前机器人末端位置，xd(t)为期望机器人末端位置，为xd(t)的导数；为x(q)的导数且jy(q)表示机器人雅各比矩阵；q
min
表示机器人最小关节位置，q
max
表示机器人最大关节位置，h(q)表示控制障碍函数，表示h(q)的导数，α(h(q))表示单调递增函数，且α(0)＝0。
[0023]
对进行数值积分获得安全的机器人关节位置q
safe
。
[0024]
所述的第三步中，采用pid控制模型跟踪安全的机器人关节位置，第四步中采用采用pid控制模型跟踪机器人动力学估计模型。
[0025]
所述的pid控制模型的输入为
[0026][0027]
其中，k
p
，kd，ki为需要设计的控制参数，在跟踪过程中，将控制时间[0,t
*
]离散成n个时刻tj，j＝1,2,...,n，在每个时刻反馈当前机器人关节位置q(tj)，更新控制输入从而完成轨迹跟踪，在整个控制过程中，每个时刻的关节位置q(tj)，关节速度pid控制输入u
pid
(tj)作为高斯回归训练数据的输入值模型误差数据作为训练数据的输出值并保存数据集[x
train
,y
train
]。
[0028]
所述的第六步中，进行高斯过程回归的方法为：
[0029]
每次选取100组连续数据进行训练，通过训练结果，对当前机器人
关节位置下模型误差进行预测，预测结果表示为：关节位置下模型误差进行预测，预测结果表示为：其中表示预测均值，δ表示预测方差，k与置信区间的选取相关，基于模型误差数据的预测结果，为保存的数据集[x
train
,y
train
]中的第i个子集。
[0030]
所述的第七步中，采用轨迹跟踪二次规划模型获得满足安全约束的控制指令。
[0031]
所述的轨迹跟踪二次规划模型为：
[0032][0033][0034]umin
≤u≤u
max
[0035]
其中，k1》0，k2》0，lf和lg表示机器人沿和的李导数，此时h(q)是一个二阶的控制障碍函数，表示模型误差导数；u
safe
是满足安全约束的控制指令，u
min
，u
max
分别表示控制输入的最大值和最小值。
[0036]
与现有技术相比，本发明提供了一种在机器人动力学模型不精确情况下，基于控制障碍函数实现安全控制的方法，且该方法具有以下显著优点：
[0037]
(1)本发明的基于控制障碍函数的模型不确定机器人安全控制方法，将机器人安全控制中的轨迹规划任务和轨迹跟踪任务相结合，在获得机器人安全关节位置后通过求解安全控制指令实现轨迹跟踪，全程满足安全约束，具有更强的安全性；
[0038]
(2)本发明的基于控制障碍函数的模型不确定机器人安全控制方法中，使用二次规划模型，可以在不依赖机器人模型的情况下获得机器人安全的关节位置；
[0039]
(3)本发明的基于控制障碍函数的模型不确定机器人安全控制方法中，使用高斯过程训练数据保存方法，相较于随机选取训练数据，模型误差估计结果具有更高的置信度；
[0040]
(4)本发明的基于控制障碍函数的模型不确定机器人安全控制方法中，使用高斯过程预测模型误差的方法，可以使用较少的数据快速得到模型误差估计值，以较高置信度获得机器人动力学精确模型；
[0041]
(5)本发明的基于控制障碍函数的模型不确定机器人安全控制方法中，使用轨迹跟踪二次规划模型，控制障碍函数相关的约束条件结合机器人模型误差估计值实现安全的轨迹跟踪，计算效率高，易于实现。
附图说明
[0042]
图1是实施例中机械臂末端执行器轨迹规划仿真结果图；
[0043]
图2是实施例中机械臂末端执行器有无安全约束条件下运动轨迹仿真结果对比图；
[0044]
图3是实施例中保证安全性的控制输入仿真结果图；
[0045]
图4为三自由度平面机械臂结构示意图。
具体实施方式
[0046]
下面结合附图和实施例对本发明做进一步说明。
[0047]
基于控制障碍函数的模型不确定机器人安全控制方法，该方法的步骤包括：
[0048]
第一步，建立机器人动力学估计模型；
[0049]
第二步，采用二次规划模型获得满足安全约束的机器人关节速度，并对机器人关节速度进行数值积分，从而获得安全的机器人关节位置；
[0050]
第三步，采用pid控制模型跟踪第二步获得的安全的机器人关节位置，得到跟踪过程中的机器人关节速度、机器人关节加速度和机器人关节力矩；
[0051]
第四步，采用pid控制模型跟踪第一步建立的机器人动力学估计模型，得到跟踪过程中的模型关节加速度；
[0052]
第五步，求取第三步得到的机器人关节加速度与第四步得到的模型关节加速度的差值，得到模型误差数据；
[0053]
第六步，根据第三步得到的机器人关节速度、机器人关节加速度和机器人关节力矩以及第五步得到的模型误差数据进行高斯过程回归，得到机器人动力学精确模型；
[0054]
第七步，对第六步得到的机器人动力学精确模型采用轨迹跟踪二次规划模型获得满足安全约束的控制指令，并将获得的满足安全约束的控制指令对机器人进行安全控制，完成基于控制障碍函数的模型不确定机器人安全控制。
[0055]
所述的第一步中，建立的机器人动力学估计模型如下：
[0056][0057]
其中，表示n个关节的位置，是机器人的惯性矩阵，表示离心力与科氏力矩阵，表示重力项，表示重力项，分别为m(q)，g(q)的估计值，为模型误差；u为控制输入；
[0058]
所述的第二步中，二次规划模型为：
[0059][0060][0061]qmin
≤q≤q
max
[0062]
其中，表示满足安全约束的机器人关节速度，q表示当前机器人关节位置；表示当前机器人关节速度，表示期望关节速度，e＝x(q)-xd(t)表示机器人末端位置跟踪误差，t表示当前时间，γ》0，γ为一常数，是一设定值，表示伪逆矩阵；x(q)为当前机器人末端位置，xd(t)为期望机器人末端位置，为xd(t)的导数；为x(q)的导数且jy(q)表示机器人雅各比矩阵；q
min
表示机器人最小关节位置，q
max
表示机器人最大关节位置，h(q)表示控制障碍函数，表示h(q)的导数，α(h(q))表示单调递增函数，且α(0)＝0；
[0063]
对进行数值积分获得安全的机器人关节位置q
safe
；
[0064]
所述的第三步和第四步中，pid控制模型的输入均为
[0065][0066]
其中，k
p
，kd，ki为需要设计的控制参数，在跟踪过程中，将控制时间[0,t
*
]离散成n个时刻tj，j＝1,2,...,n，在每个时刻反馈当前机器人关节位置q(tj)，更新控制输入从而完成轨迹跟踪，在整个控制过程中，每个时刻的关节位置q(tj)，关节速度pid控制输入u
pid
(tj)作为高斯回归训练数据的输入值模型误差数据作为训练数据的输出值并保存数据集[x
train
,y
train
]；
[0067]
所述的第六步中，进行高斯过程回归的方法为：
[0068]
每次选取100组连续数据进行训练，通过训练结果，对当前机器人关节位置下模型误差进行预测，预测结果表示为：关节位置下模型误差进行预测，预测结果表示为：其中表示预测均值，δ表示预测方差，k与置信区间的选取相关，基于模型误差数据的预测结果，为保存的数据集[x
train
,y
train
]中的第i个子集；
[0069]
所述的第七步中，轨迹跟踪二次规划模型为：
[0070][0071][0072]umin
≤u≤u
max
[0073]
其中，k1》0，k2》0，lf和lg表示机器人沿和的李导数，此时h(q)是一个二阶的控制障碍函数，表示模型误差导数；u
safe
是满足安全约束的控制指令，u
min
，u
max
分别表示控制输入的最大值和最小值。
[0074]
实施例
[0075]
本发明选取三自由度平面机械臂末端执行器运动过程中的避障问题作为实施例，结合附图详述如下：
[0076]
选取如图4所示的三自由度平面机械臂，各个关节的结构参数为：m1＝1kg，m2＝0.8kg，m3＝0.6kg，l1＝1m，l2＝0.8m，l3＝0.6m。机械臂末端执行器从起始点(-0.12,2.4)处沿直线到达终点(-1.44,1.84)，在点(-1,2)处存在一个半径为0.1m的圆形障碍物，为保证末端执行器安全，需要避开障碍物并尽量小的偏离原轨迹。
[0077]
为了实现此任务，具体步骤如下：
[0078]
a.构建三自由度平面机械臂动力学估计模型：
[0079][0080]
其中，设定为三阶单位矩阵，
且
[0081]
b.基于控制障碍函数，采用如下二次规划方法获得运动速度
[0082][0083][0084]qmin
≤q≤q
max
[0085]
其中，其中，其中，γ＝diag[27,8]，h(q)＝(x1(q)+1)2+(x2(q)-2)
2-0.01，α(h(q))＝h(q)，q
min
＝-50，q
max
＝50。
[0086]
对进行数值积分获得安全的机器人关节位置q
safe
；
[0087]
如附图1所示，当机械臂按照角度q
safe
运动时，路径完全避开障碍物并且最小的偏离原定轨迹。
[0088]
c.采用如下pid控制模型的输入跟踪关节运动角度q
safe
，
[0089][0090]
其中，k
p
＝diag[800,800,200]，kd＝diag[90,10,11]，ki＝diag[10,10,0.35]。将控制时间[0,20]离散成n个时刻tj，j＝1,2,...,n，n＝2000，在每个时刻反馈当前机器人关节位置q(tj)，更新控制输入从而完成轨迹跟踪。在整个控制过程中，每个时刻的关节位置q(tj)，关节速度pid控制模型的输入u
pid
(tj)作为高斯回归训练数据的输入值模型误差数据保存为训练数据的输出值当pid控制结果存在微小误差时就可能使末端执行器处于不安全位置，如附图2中单独使用pid控制模型的运动轨迹所示。
[0091]
d.对保存的数据集[x
train
,y
train
]，每次选取连续的100组数据采用gpml工具箱进行模型训练，并根据训练结果获得模型误差的预测平均值和方差δ。
[0092]
e.在pid控制模型的基础上采用如下轨迹跟踪二次规划模型，加入控制障碍函数h(q)＝(x1(q)+1)2+(x2(q)-2)
2-0.01作为约束求解安全控制指令u
safe
：
[0093][0094][0095]umin
≤u≤u
max
[0096]
其中，k1＝20，k2＝30，k＝2，此时置信度为95％。lf和lg表示机器人沿和的李导数，u
min
＝[-50
ꢀ‑
50
ꢀ‑
50]
t
，u
max
＝[50 50 50]
t
。
[0097]
通过以上步骤，求解出满足安全约束的控制指令u
safe
使得运动轨迹仿真结果如图2所示，末端执行器完全避开障碍物，满足安全性要求，并且图3表示u
safe
在区间[u
min
,u
max
]内，不会导致关节角度过饱和的问题。