一种多段连续体机械臂形态预测方法

1.本发明属于机械臂形态预测领域，具体涉及一种多段连续体机械臂形态预测方法。


背景技术：

2.连续体机械臂是一类由弹性材料构成的可实现连续变形的机械臂，其理论上具有无限自由度。相比于刚性机械臂，连续体机械臂具有更强的灵活性以及人机交互安全性，且在空间航天器、微创手术和救援维修等领域都得到了应用。
3.连续体机械臂的自由度和驱动数目较多，如何对其形态进行精确控制是连续体机械臂实际应用中不可避免的问题，而形态预测更是最为关键的一步。目前在形态检测领域大都使用外部传感器对机械臂形态直接重构，一些学者将基于分段常曲率假设的模型引入用以得到更加精确的结果，但大部分研究对象都是单段连续体机械臂，而在连续体机械臂的实际应用中，往往采用多段串联的方式用以实现复杂的形态。
4.为了达到预期的控制精度，需要辅以精确的模型描述，分段常曲率虽然使用较为广泛，如公布号为cn112828893a和cn114012728a的发明专利便采用了分段常曲率假设对多段机械臂进行了静力学和运动学分析，但其局限在于一旦机械臂有外部载荷的参与，这一假设便不再成立。力学中常用的有限元方法虽然可以对任意载荷下的机械臂变形进行求解，但计算复杂，且机械臂几何结构的任一微小改动都需要重新划分网格，时间成本过高。cosserat杆模型可以精确描述连续体的拉压、剪切、扭转和弯曲变形，能够弥补常曲率假设的不足，对多段连续体机械臂精确描述来说是较为理想的选择。
5.结合上述情况，对于多段连续体机械臂，需要一种结合cosserat杆模型的高精度形态预测方法，兼顾计算效率和精度，能够根据驱动丝位移输入直接求解机械臂形态。


技术实现要素：

6.本发明目的在于提供一种多段连续体机械臂形态预测方法。
7.实现上述目的的技术解决方案为：
8.一种多段连续体机械臂形态预测方法，包括以下步骤：
9.步骤1、基于cosserat杆理论，建立单段连续体机械臂的几何描述及静力学模型；
10.步骤2、通过组合单段连续体机械臂，建立多段连续体机械臂的几何描述和静力学模型；
11.步骤3、考虑多段连续体机械臂中前一段机械臂形态变化对后一段机械臂所属驱动丝的位移量的影响，建立每段机械臂的驱动丝有效位移量的概念，并给出每段机械臂的驱动丝有效位移量的求解公式；
12.步骤4、根据力的平衡方程和几何方程，给出各段机械臂形态求解时初值条件的迭代公式；
13.步骤5、基于多段连续体机械臂的静力学模型，结合步骤4的初值条件迭代公式和
驱动丝有效位移量的求解公式，依次求解各段机械臂形态，建立驱动器输入量与形态映射关系。
14.本发明与现有技术相比，其显著优点为：
15.(1)能够直接通过驱动器输入量预测多段机械臂形态，无需其它传感器辅助；
16.(2)使用了cosserat杆模型进行静力学建模，相比于常曲率假设精度更高并且可考虑外部载荷对机械臂的影响，方法适用于任意段数和驱动丝数的机械臂；
17.(3)同有限元法相比，本发明的计算速度更快，且与有限元法的误差仅为机械臂长度的3.05％。
18.下面结合附图和具体实施方式对本发明作进一步的详细描述。
附图说明
19.图1为本发明多段连续体机械臂形态预测方法的几何描述图；
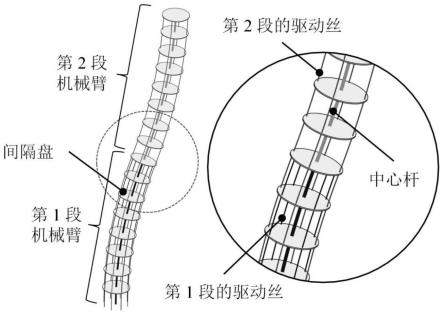
20.图2为本发明的实施实例的两段式连续体机械臂的结构组成图；
21.图3是本发明的实施实例的驱动器输入量示意图；
22.图4是本发明的实施实例的驱动丝沿机械臂截面分布图；
23.图5是本发明的实施实例结果与有限元方法的对比图。图6为本发明预测的两段机械臂形态与有限元法求解结果的对比图。
具体实施方式
24.现针对两段式连续体机械臂的实施实例，对本发明作进一步描述。
25.步骤1、基于cosserat杆理论，建立单段连续体机械臂的几何描述及静力学模型：
26.步骤1-1：如图1所示，定义p(s)为随机械臂中心杆弧长s变化的三维笛卡尔曲线,r(s)为随机械臂中心杆弧长s变化的三维旋转矩阵。图2所示为驱动丝在中心杆截面出局部坐标系下的位置，据此定义第i根驱动丝的空间位置为
27.pi(s)＝r(s)ri(s)+p(s)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(1)
28.其中ri(s)为驱动丝在中心杆截面上的分布。
29.步骤1-2：根据图3的力和力矩平衡关系，得到力平衡方程，可求得
[0030][0031]
其中符号表示对s的一阶导数；符号
*
代表各项变量的初始值；为u的反对称矩阵；v(s)和u(s)为线性应变和角性应变；l(s)和f(s)为分布力矩和分布力；k
se
和k
bt
为相应刚度矩阵；
[0032]
步骤1-3：结合步骤1-2中公式(1)和(2)，引入驱动丝与中心杆之间的耦合关系，得到驱动丝对中心杆的力和力矩为
[0033][0034]
其中τi为第i根驱动丝的拉力。
[0035]
同时定义中间变量如下：
[0036][0037][0038][0039][0040][0041]
其中符号(
·
)b表示该变量在局部坐标系下的表达形式，n为驱动丝数量。
[0042]
步骤1-4：结合以上步骤及其中公式，建立单段连续体机械臂静力学模型为：
[0043][0044]
其中
[0045][0046][0047]
步骤2、通过组合单段连续体机械臂，建立如图2所示的多段连续体机械臂的几何描述和静力学模型：
[0048]
多段连续体机械臂中心杆的空间位置和对应旋转矩阵可写为
[0049][0050]
其中，代表第k段机械臂的空间位置分布，代表第k段机械臂的旋转矩阵分布，s的取值范围为[∫lk,∫l
k+1
]，lk为第k段机械臂的长度，∫lk为前k段机械臂的长度之和；为前k段机械臂的空间分布；为前k段机械臂的姿态矩阵分布；
[0051]
为了便于每一段的姿态计算，额外定义
[0052][0053]
此时δ的取值范围为[0,lk]。
[0054]
定义驱动丝的空间位置
[0055][0056]
p
k,i
(s)为第k段的第i根驱动丝的空间分布；代表第k段的空间位置分布；r
k,i
(s)为控制第k段的第i根驱动丝在中心杆截面局部坐标下的位置；
[0057]
定义为第k段的所有驱动丝的驱动器输入量，是第k段的第i根驱动丝的驱动器输入量；
[0058][0059]
步骤3、考虑多段连续体机械臂中前一段机械臂形态变化对后一段机械臂所属驱动丝的位移量的影响，建立每段机械臂的驱动丝有效位移量的概念，并给出每段机械臂的驱动丝有效位移量的求解公式：
[0060]
结合公式(7)，对于第k段机械臂的第i根驱动丝，其有效位移量的计算公式如下：
[0061][0062]
其中q
k,i
为是第k段的第i根驱动丝的有效位移量，类比公式(8)，可以得到qk为第k段的所有驱动丝的有效位移量。
[0063]
步骤4、根据力的平衡方程和几何方程，结合公式(6)的定义，给出各段机械臂形态求解时初值条件的迭代公式：
[0064][0065]
其中0
k+1
为第k+1段机械臂起始位置。
[0066]
步骤5、基于多段连续体机械臂的静力学模型，结合上述步骤的静力学模型和形态求解的迭代公式，依次求解各段机械臂形态，建立驱动器输入量与形态映射关系，其求解过程如下：
[0067]
1)对于k段连续体机械臂，根据公式(8)的定义，给定期望的驱动器输入量给定各段的空间位置初值旋转矩阵
[0068]
2)对于第1段机械臂，结合公式(7)、(8)、(9)，其驱动丝有效位移量根据公式(10)可得其初值条件为将二者代入式(4)，即可得到第1段形态与
[0069]
3)对于第2段机械臂，结合公式(7)、(8)、(9)计算第2段的驱动丝有效位移量q2，再根据式(10)计算第2段机械臂的初值条件，将二者代入式 (4)，计算即可得到第2段形态和
[0070]
4)以此类推，直至求得全部k段机械臂的形态，根据公式(5)将其组合，最终得到多段连续体机械臂的形态和
[0071]
如图4所示，计算实例的机械臂本体共有k＝2段，由中心杆、间隔盘和驱动丝构成，第2段的驱动丝穿过第1段。两段机械臂的长度l1＝l2＝l，中心杆上分布有若干间隔盘。
[0072]
如图5所示，每段机械臂都有n＝4根驱动丝控制，驱动丝在驱动器输入量下产生位移，驱动机械臂实现不同形态。两段的驱动丝都沿圆周均布，驱动丝到中心杆中心的偏距为l
off
＝0.023m。
[0073]
计算实例中，给定中心杆初始形态为
[0074][0075]
驱动器输入量为
[0076][0077]
两段机械臂的驱动丝在局部坐标下的分布为
[0078][0079][0080]
按以下步骤进行形态预测：
[0081]
步骤1、基于cosserat杆理论，建立单段连续体机械臂的几何描述及静力学模型如公式(4)。
[0082]
步骤2、通过组合单段连续体机械臂，建立如图2所示的两段连续体机械臂的几何描述为
[0083][0084][0085][0086]
其中，p(s)为随机械臂中心杆弧长s变化的三维笛卡尔曲线，p
12
(s)代表第 2段的空间位置分布，p
02
(s)为两段机械臂整体的空间分布；r(s)为随机械臂中心杆弧长s变化的三维旋转矩阵，上下标定义同p(s)；p
k,i
(s)为第k段的第i根驱动丝的空间分布；r
k,i
(s)为控制第k段的第i根驱动丝在中心杆截面局部坐标下的位置；和为第1段和第2段的驱动丝的驱动器输入量；
[0087]
步骤3、考虑多段连续体机械臂中前一段机械臂形态变化对后一段机械臂所属驱动丝的位移量的影响，建立每段机械臂的驱动丝有效位移量的概念，并给出每段机械臂的驱动丝有效位移量的求解公式：
[0088][0089]
其中q
2,i
为是第2段的第i根驱动丝的有效位移量，l
10
为前1段中心杆的长度。
[0090]
步骤4、根据力的平衡方程和几何方程，给出各段机械臂形态求解时初值条件的迭代公式：
[0091]
p2(02)＝p1(l1)
ꢀꢀꢀꢀꢀꢀꢀꢀ
(15)
[0092]
r2(02)＝r1(l1)
[0093]
其中，l1为第1段机械臂的长度。
[0094]
步骤5、基于多段连续体机械臂的静力学模型，结合上述步骤的静力学模型和形态求解的迭代公式，依次求解各段机械臂形态，建立驱动器输入量与形态映射关系，其求解过程为：
[0095]
1)给定期望的驱动器输入量为给定各段的空间位置初值旋转矩阵
[0096]
2)对于第1段机械臂，根据公式(12)、(13)、(14)可计算驱动丝有效位移量其初值条件为将二者代入式(4)，即可得到第1段形态与
[0097]
3)对于第2段机械臂，根据公式(12)、(13)、(14)可计算第2段的驱动丝有效位移量q2，再根据式(15)计算第2段机械臂的初值条件，将二者代入式(4)，计算即可得到第2段形态p
12
和r
12
；
[0098]
4)根据公式(11)将其组合可得到多段连续体机械臂的形态p
02
和
[0099]
图6为上述实例所预测的两段机械臂形态与有限元法求解结果的对比图，可以看到二者差别很小，末端位置误差仅为两段机械臂长度的3.05％。
[0100]
由上述实例可知，本发明的建模方法可以根据驱动器输入量准确预测多段机械臂形态；通过引入cosserat杆模型突破了常曲率假设的限制，实现了准确且高效的形态预测。在实现了与有限元法接近的解算精度的同时，本发明的解算时间相比于有限元法也大大缩短，为多段机械臂的实时形态预测与控制提供了基础。
[0101]
以上显示和描述了本发明的基本原理、主要特征及优点。本行业的技术人员应该了解，本发明不受上述实施例的限制，上述实施例和说明书中描述的只是说明本发明的原理，在不脱离本发明精神和范围的前提下，本发明还会有各种变化和改进，这些变化和改进都落入要求保护的本发明范围内。本发明要求保护范围由所附的权利要求书及其等效物界定。