一种递推式的机器人双臂协同作业路径规划方法与流程

1.本发明属于机器人控制技术领域，具体涉及一种递推式的机器人双臂协同作业路径规划方法。


背景技术：

2.随着机器人技术的发展，将串联机器人装载于传统工程机械或机床的末端，利用机器人的灵活性和高精度以及工程机械的高负载和大范围移动的能力，用于实现在大范围移动空间中的精密作业成为发展趋势，如飞机机身加工、高铁车身打磨、船体外观焊接等。除了在车间环境内进行机械加工，该类设备也可用高危行业的户外高空作业，如户外架空线路带电抢修作业、爆破炸药填充等。
3.该类设备控制是其实现功能的关键技术。该控制的实现流程是通过高精度测量，获取作业目标点空间位置，之后通过工程机械或者机床的末端高精度定位将机械臂移动至目标作业点，在通过机械臂自身的目标跟踪与控制实现机械臂末端与作业点的高精度交互。
4.然而，目前常见的路径规划都是基于视觉信息进行单臂机器人末端的路径规划，对于双臂型的机器人执行双臂协同作业任务时的路径规划尚无可行方法。


技术实现要素：

5.有鉴于此，本发明旨在解决目前基于视觉信息进行单臂机器人末端的路径规划的方法无法适用于双臂型机器人执行双臂协同作业任务时的路径规划的问题。
6.为了解决上述技术问题，本发明提供以下技术方案：
7.本发明提供了一种递推式的机器人双臂协同作业路径规划方法，包括：
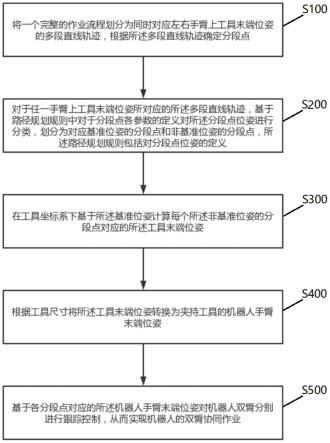
8.将一个完整的作业流程划分为同时对应左右手臂上工具末端位姿的多段直线轨迹，根据多段直线轨迹确定分段点；
9.对于任一手臂上工具末端位姿所对应的多段直线轨迹，基于路径规划规则中对于分段点各参数的定义对分段点位姿进行分类，划分为对应基准位姿的分段点和非基准位姿的分段点，路径规划规则包括对分段点位姿的定义；
10.在工具坐标系下基于基准位姿计算每个非基准位姿的分段点对应的工具末端位姿；
11.根据工具尺寸将工具末端位姿转换为夹持工具的机器人手臂末端位姿；
12.基于各分段点对应的机器人手臂末端位姿对机器人双臂分别进行跟踪控制，从而实现机器人的双臂协同作业。
13.进一步的，路径规划规则具体包括：动作序号定义；
14.动作序号定义包括对应于基准位姿、基准前位姿和基准后位姿的序号定义；
15.基准位姿为计算基准，基准前位姿为基于基准位姿、且发生于机器人手臂末端装载的工具末端抵达基准位姿前所将途径的多段线上分段点的位姿，基准后位姿为基于基准
位姿、且发生于机器人手臂末端装载的工具末端抵达基准位姿后所将途径的多段线上分段点的位姿。
16.进一步的，路径规划规则还包括：动作参考坐标系定义；
17.动作参考坐标系定义包括对应于绝对坐标系下绝对值、绝对坐标系下相对值和工具坐标系下相对值的序号定义；
18.绝对坐标系下绝对值为在机器人坐标系中的某个具体位置和姿态，绝对坐标系下相对值为在机器人坐标系下，相对于某一个基准点的6维距离，工具坐标系下相对值为在机器人手臂末端工具的坐标系下，相对于某一个基准点的6维距离。
19.进一步的，路径规划规则还包括：动作参考信号来源；
20.动作参考信号来源包括对应于手动输入、左臂视觉定位、右臂视觉定位、左臂工具坐标和右臂工具坐标的序号定义。
21.进一步的，路径规划规则还包括：动作变动增量；
22.动作变动增量为6维数组，数组内部变量定义依次为当前分段点对应三维坐标系下的三个正交位置坐标和对应的旋转角度坐标。
23.进一步的，基于路径规划规则中对于分段点各参数的定义对分段点位姿进行分类，具体包括：
24.当左臂或者右臂的动作序号对应为基准位姿，且动作参考坐标系序号对应为绝对坐标系下绝对值时，分段点对应为基准位姿，记为第一类分段点；
25.当左臂或者右臂的动作序号对应为基准位姿，动作参考坐标系序号对应为工具坐标系下相对值，且动作参考信号来源为左臂视觉定位或者右臂视觉定位时，分段点对应为基准位姿，记为第二类分段点；
26.当左臂或者右臂的动作序号对应为基准位姿，动作参考坐标系序号对应为工具坐标系下相对值，且动作参考信号来源为左臂工具坐标和右臂工具坐标时，分段点对应为基准位姿，记为第三类分段点；
27.当左臂或者右臂的动作序号对应为非基准位姿时，按照相对位姿变换公式计算当前分段点对应的位姿。
28.进一步的，各类对应于基准位姿的分段点的基准来源具体为：
29.第一类分段点的基准来源为外部输入的绝对位姿；
30.第二类分段点的基准来源为外部视觉信号输入的绝对位姿；
31.第三类分段点的基准来源为对应右臂或者左臂分段点对应的位姿。
32.进一步的，各类对应于基准位姿的分段点的动作变动增量的数值具体为：
33.第一类分段点的动作变动增量的数值为绝对位姿值；
34.第二类分段点的动作变动增量的数值为在视觉信号输入量基础上的偏差值；
35.第三类分段点的动作变动增量的数值为在分段点基础上的偏差值。
36.进一步的，相对位姿变换公式具体如下：
37.p4×4＝t(x0,y0,z0)rz(rz0)ry(ry0)rx(rx0)t(x
δ
,y
δ
,z
δ
)rx(rx
δ
)ry(ry
δ
)rz(rz
δ
)
38.式中，p4×4为当前分段点对应的位姿，x，y，z分别表示机器人末端在相应坐标系下，绕x，y，z轴的平动距离；rx，ry，rz分别表示机器人末端在相应坐标系下，绕x，y，z轴的转动角度；下标为0时表示相对基准数值，为δ时表示变化量。
39.进一步的，根据工具尺寸将工具末端位姿转换为夹持工具的机器人手臂末端位姿，具体按照下式进行转换：
40.p
′4×4＝p4×4t(x
tool
,y
tool
,z
tool
)
41.式中，p'4×4为转换后的机器人手臂末端位姿，t(x
tool
,y
tool
,z
tool
)为工具的三维尺寸。
42.综上，本发明提供了一种递推式的机器人双臂协同作业路径规划方法，包括将一个完整的作业流程划分为多段直线轨迹，基于路径规划规则对多段直线轨迹上的分段点，在工具坐标系下基于基准位姿计算每个非基准位姿的分段点对应的工具末端位姿；根据工具尺寸将工具末端位姿转换为夹持工具的机器人手臂末端位姿；基于各分段点对应的机器人手臂末端位姿对机器人双臂分别进行跟踪控制，从而实现机器人的双臂协同作业。本发明通过将机器人动作规划设计成递推过程，每一个递推过程存在一个基准位姿，基于该基准位姿完成从工具位姿到机器人位姿的转换，从而实现机器人双臂的协同作业。
附图说明
43.为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其它的附图。
44.图1为本发明实施例提供的一种递推式的机器人双臂协同作业路径规划方法的流程图；
45.图2为本发明实施例提供的某一机器人双臂协同进行安装作业前的位姿示意图；
46.图3为本发明实施例提供的某一机器人双臂协同进行安装作业后的位姿示意图；
47.图4为本发明实施例提供的零件3的尺寸示意图。
具体实施方式
48.为使得本发明的目的、特征、优点能够更加的明显和易懂，下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，下面所描述的实施例仅仅是本发明一部分实施例，而非全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其它实施例，都属于本发明保护的范围。
49.随着机器人技术的发展，将串联机器人装载于传统工程机械或机床的末端，利用机器人的灵活性和高精度以及工程机械的高负载和大范围移动的能力，用于实现在大范围移动空间中的精密作业成为发展趋势，如飞机机身加工、高铁车身打磨、船体外观焊接等。除了在车间环境内进行机械加工，该类设备也可用高危行业的户外高空作业，如户外架空线路带电抢修作业、爆破炸药填充等。
50.该类设备控制是其实现功能的关键技术。该控制的实现流程是通过高精度测量，获取作业目标点空间位置，之后通过工程机械或者机床的末端高精度定位将机械臂移动至目标作业点，在通过机械臂自身的目标跟踪与控制实现机械臂末端与作业点的高精度交互。
51.然而，目前常见的路径规划都是基于视觉信息进行单臂机器人末端的路径规划，对于双臂型的机器人执行双臂协同作业任务时的路径规划尚无可行方法。
52.基于此，本发明提供了一种递推式的机器人双臂协同作业路径规划方法，包括如下步骤：
53.s100：将一个完整的作业流程划分为同时对应左右手臂上工具末端位姿的多段直线轨迹，根据多段直线轨迹确定分段点。
54.本实施例提供的递推式路径规划方法由规划规则和规划算法两部分组成。规划规则包括了动作序号定义、动作参考坐标系定义、动作参考信号来源、动作变动增量四部分组成；规划算法包括了工具末端位姿计算算法、工具末端位姿向机器人手臂末端变换算法等两部分组成。在该规划方法作用下，一个完整的作业流程被划分为同时对应左右手臂末端位姿的多段直线轨迹，通过生成多段线上的分段点处机器人的双臂末端位姿，实现对机器人运动轨迹的控制。
55.s200：对于任一手臂上工具末端位姿所对应的多段直线轨迹，基于路径规划规则中对于分段点各参数的定义对分段点位姿进行分类，划分为对应基准位姿的分段点和非基准位姿的分段点，路径规划规则包括对分段点位姿的定义。
56.在本实施例中，路径规划规则中的各部分可以定义如下：
57.1)动作序号定义
[0058]“0”：基准位姿。基准位姿为一个计算基准，该基准对应的数据由信号源直接提供或在信号源提供数据上仅处理一次后的数据。
[0059]
“‑
1”、
“‑2”……“‑
n”：基准前位姿。是基于基准位姿且发生于机器人手臂末端装载的工具末端抵达基准位姿前所将途径的多段线上分段点的位姿。
[0060]“1”、“2
”……“
n”：基准后位姿。是基于基准位姿且发生于机器人手臂末端装载的工具末端抵达基准位姿后所将途径的多段线上分段点的位姿。
[0061]
δp1×6:动作变动增量。为6维数组，数组内部变量定义依次为当前分段点对应三维坐标系下的三个正交位置坐标和对应的旋转角度坐标。
[0062]
2)坐标系定义
[0063]“1”：绝对坐标系下绝对值。在机器人坐标系中的某个具体位置和姿态。
[0064]“2”：绝对坐标系下相对值。在机器人坐标系下，相对于某一个基准点的6维距离(包含位置与姿态)。
[0065]“3”：工具坐标系下相对值。在机器人手臂末端工具的坐标系下，相对于某一个基准点的6维距离(包含位置与姿态)。
[0066]
3)信号源定义
[0067]“1”：手动输入。
[0068]“2”：左臂视觉定位。
[0069]“3”：右臂视觉定位。
[0070]“4”：左臂工具坐标。
[0071]“5”：右臂工具坐标。
[0072]
4)动作变动增量
[0073]
δp1×6:动作变动增量。为6维数组，数组内部变量定义依次为当前分段点对应三维
坐标系下的三个正交位置坐标和对应的旋转角度坐标。
[0074]
基于以上定义，可形成如下规则表格
[0075][0076][0077]
基于路径规划规则计算各分段点工具末端位姿，包括分段点归类和分段点计算两部分。本步骤中结合上述定义对分段点归类进行介绍如下：
[0078]
当左(右)臂的序号为0，且坐标系定义为1时，该行为基准位姿，基准来源为手动输入的绝对位姿，动作变动变量数值为该绝对位姿数值。
[0079]
当左(右)臂的序号为0，坐标系定义为3且信号源定义为2(3)时，该行为基准位姿，基准来源为外部视觉信号输入的绝对位姿，动作变动变量数值为在该视觉信号输入量基础上的偏差值。
[0080]
当左(右)臂的序号为0，坐标系定义为3且信号源定义为4(5)时，该行为基准位姿，基准来源为该行对应的右(左)臂分段点对应的位姿，动作变动变量数值为在该分段点基础上的偏差值。即左(右)臂相对于右(左)臂在某个时刻的位姿，进行相对移动。由于机械臂本身在实际使用中会有结构误差，因此采用理想一条臂的理想位姿作为另一条臂的参考基准。
[0081]
当左(右)臂的序号为非0时，依照(2)计算对应位姿。
[0082]
s300：在工具坐标系下基于基准位姿计算每个非基准位姿的分段点对应的工具末端位姿。
[0083]
本步骤中对分段点计算做出介绍如下：
[0084]
首先定义旋转矩阵：
[0085][0086][0087]
则，在工具坐标系下基于基准位姿，进行相对位姿变换可得当前分段点对应的位
姿为：
[0088]
p4×4＝t(x0,y0,z0)rz(rz0)ry(ry0)rx(rx0)t(x
δ
,y
δ
,z
δ
)rx(rx
δ
)ry(ry
δ
)rz(rz
δ
)
[0089]
其中，x，y，z分别表示机器人末端在相应坐标系下，绕x，y，z轴的平动距离；rx，ry，rz分别表示机器人末端在相应坐标系下，绕x，y，z轴的转动角度；下标“0”代表相对基准数值，下标“δ”代表变化量，δp1×6＝[x
δ
,y
δ
,z
δ
,rx
δ
,ry
δ
,rz
δ
]。进一步可得：
[0090]
x1＝p
1,4
，y1＝p
2,4
，z1＝p
3,4
[0091]
rx1＝atan2(p
3,2
,p
3,3
)，ry1＝atan2(-p
3,1
,√p
3,22
+p
3,32
)，rz1＝atan2(p
2,1
,p
1,1
)
[0092]
下标“1”为当前计算所得数值，双下标“i，j”表示矩阵的第i行第j列元素。
[0093]
s400：根据工具尺寸将工具末端位姿转换为夹持工具的机器人手臂末端位姿。
[0094]
当求得当前分段点末端工具坐标后，可根据工具尺寸，球的加持工具的机器人手臂末端位姿。计算公式如下：
[0095]
p
′4×4＝p4×4t(x
tool
,y
tool
,z
tool
)
[0096]
其中下标“tool”表示工具外观尺寸。至此便可求得每一个分段点对应的手臂末端位姿，用于跟踪控制。
[0097]
s500：基于各分段点对应的机器人手臂末端位姿对机器人双臂分别进行跟踪控制，从而实现机器人的双臂协同作业。
[0098]
以下结合实例对本实施例提出的递推式路径规划方法进行介绍。
[0099]
以机器人将零件1、2和3进行安装过程为例，安装前后零件与机器人相对位置如图2所示。如图3所示，安装后要求零件2与零件1空间平行、零件1上安装点1与零件3上固定点1重合、零件2上安装点2与零件3上固定点2重合。作业前机器人左臂末端夹持零件2、右臂末端夹持零件3。通过视觉等非接触定位方法，可确定零件1空间姿态和安装点1空间位置；并确定零件2空间姿态和安装点2空间位姿。零件3结构尺寸已知，如图4所示。为简化描述，令z恒等于0，零件3无厚度，动作流程为x-y平面运动。
[0100]
针对该作业，可设计规则表格如下：
[0101][0102][0103]
基于以上规则：
[0104]
第一步：左臂和右臂首先分别以p
1l
和p
1r
位姿预备；
[0105]
第二步：右臂根据第三步对应的位姿，在x轴方向移动移动δx
r1
。左臂根据第一步位姿，在y方向移动δy
l1
。
[0106]
第三步：右臂根据视觉反馈的零件1姿态和安装点1位姿，将零件3上固定点1和2连线与零件1垂直，并在位置上相对于安装点1位姿在x方向上移动-l
1-l2。左臂根据第四步中
左臂的位姿在x方向上移动δx
l2
。该步移动后，安装点1与固定点1重合，安装点2与固定点2未重合，但零件2与零件1平行。
[0107]
第四步：右臂静止。左臂根据右臂对应的零件1姿态和安装点位姿，将零件2与零件1平行，并将安装点2与固定点2重合。至此零件安装完毕。
[0108]
本实施例提出一种递推式的机器人双臂协同作业路径规划方法，包括将一个完整的作业流程划分为多段直线轨迹，基于路径规划规则对多段直线轨迹上的分段点，在工具坐标系下基于基准位姿计算每个非基准位姿的分段点对应的工具末端位姿；根据工具尺寸将工具末端位姿转换为夹持工具的机器人手臂末端位姿；基于各分段点对应的机器人手臂末端位姿对机器人双臂分别进行跟踪控制，从而实现机器人的双臂协同作业。本发明通过将机器人动作规划设计成递推过程，每一个递推过程存在一个基准位姿，基于该基准位姿完成从工具位姿到机器人位姿的转换，从而实现机器人双臂的协同作业。
[0109]
与现有技术相比，本实施例提出的方法具有如下优点：
[0110]
该方法可以接入不同的定位信号源。计算方法与信号来源无关。
[0111]
该方法将双臂动作同步化，可以增加不同的控制参数，比如力控制下，每一个分段点可以配置不同的刚度阻尼参数。
[0112]
将双臂动作协调至同一个坐标系下。无论是视觉定位输入还是双臂交叉参考，双臂始终都在同一个坐标系下动作，具有扩展成复杂协同作业的能力。
[0113]
以上实施例仅用以说明本发明的技术方案，而非对其限制；尽管参照前述实施例对本发明进行了详细的说明，本领域的普通技术人员应当理解：其依然可以对前述各实施例所记载的技术方案进行修改，或者对其中部分技术特征进行等同替换；而这些修改或者替换，并不使相应技术方案的本质脱离本发明各实施例技术方案的精神和范围。