基于关节全闭环和刚柔耦合模型的机器人精度提升方法和系统与流程

1.本发明涉及机器人技术领域，具体地，涉及一种基于关节全闭环和刚柔耦合模型的机器人精度提升方法和系统。


背景技术：

2.工业机器人具有较好的重复定位精度，但是由于标准工业机器人各关节采用半闭环控制，且关节和连杆刚性较差，工业机器人的绝对定位精度比较低。为满足航空高位置精度制孔要求，需要进一步提升机器人绝对定位精度。
3.专利文献cn107457785a(申请号：cn201710881683.x)公开了一种基于机器人关节反馈的机器人的位置补偿方法，该方法使用的装置包括绝对式光栅尺、适配器和计算机。绝对式光栅尺分别安装在机器人的各个关节轴上，光栅尺的读数头读取信号经过适配器转换连接到计算机，在上位机中对适配器进行二次开发，同时读取多个光栅的反馈信号并根据标定的模型生成关节的转角值，通过建立的空间误差估计模型和误差耦合模型将空间误差转化成为关节转角误差；此外，建立上位机与机器人的实时交互环境，通过pd控制模型，将机器人关节的转角值修正到目标值，从而实现机器人位置的补偿。然而该专利未补偿机器人连杆重力变形，精度提升有限，采用上位机和机器人进行交互控制，通讯延时会大大影响补偿和定位效率。


技术实现要素：

4.针对现有技术中的缺陷，本发明的目的是提供一种基于关节全闭环和刚柔耦合模型的机器人精度提升方法和系统。
5.根据本发明提供的基于关节全闭环和刚柔耦合模型的机器人精度提升方法，包括如下步骤：
6.步骤1：在机器人各关节安装光栅尺和读数头，将读数头的位置信号接入各轴电机的伺服控制器中，实现各个关节轴的全闭环控制；
7.步骤2：利用激光干涉仪对机器人各关节定位精度进行校准；
8.步骤3：建立机器人增强刚柔耦合运动学模型；
9.步骤4：利用激光跟踪仪对机器人增强刚柔耦合运动学模型参数进行校准；
10.步骤5：利用增强刚柔耦合运动学模型对机器人定位进行补偿。
11.优选的，所述步骤3包括：在外力f、力矩m和自身重力mg的作用下，连杆末端坐标系{ei}的变形为：
12.13.其中：x
ei
、y
ei
、z
ei
、α
ei
、β
ei
、γ
ei
为连杆在坐标系{ei}下受力的变形量。
14.优选的，建立机器人的增强刚柔耦合运动学模型，表达式为：
[0015][0016]
其中：-1
t6为法兰坐标系{6}在设备基础坐标系{-1}下的齐次变换；it
ei
为连杆末端坐标系{ei}在连杆坐标系{i}下的齐次变换；为机器人的mdh运动学参数；κ代表连杆的柔性系数；q代表机器人各轴的坐标；f()为机器人的增强刚柔耦合模型前向运动学表达式。
[0017]
优选的，所述步骤4包括：建立标定模型，表达式为：
[0018][0019]
其中：
l
t-1
为设备基础坐标系{-1}在激光跟踪仪测量坐标系{l}下的齐次变换，ψ是对应位姿参数；i3为3阶单位矩阵；6t
tool
为工具坐标系{t}在法兰坐标系{6}下的齐次变换，τ为相对应的位姿参数；bj为跟踪仪测量靶球在工具坐标系下的坐标；h()为综合标定模型表达式；l表示第l个机器人位姿；j表示第j个靶球。
[0020]
优选的，将靶球固定到机器人末端上，利用跟踪仪测量机器人若干组关节坐标对应的靶球坐标推导用于levenberg
–
marquardt算法辨识的线性标定模型，表达式为：
[0021][0022]
其中：δq为偏差矢量；j
ξ
代表雅可比矩阵；δξ代表模型参数误差；为测量坐标和名义坐标的偏差；n为标定用的机器人位姿总数量。
[0023]
根据本发明提供的基于关节全闭环和刚柔耦合模型的机器人精度提升系统，包括如下模块：
[0024]
模块m1：通过安装在机器人各关节的光栅尺和读数头，将读数头的位置信号接入各轴电机的伺服控制器中，实现各个关节轴的全闭环控制；
[0025]
模块m2：利用激光干涉仪对机器人各关节定位精度进行校准；
[0026]
模块m3：建立机器人增强刚柔耦合运动学模型；
[0027]
模块m4：利用激光跟踪仪对机器人增强刚柔耦合运动学模型参数进行校准；
[0028]
模块m5：利用增强刚柔耦合运动学模型对机器人定位进行补偿。
[0029]
优选的，所述模块m3包括：在外力f、力矩m和自身重力mg的作用下，连杆末端坐标系{ei}的变形为：
[0030][0031]
其中：x
ei
、y
ei
、z
ei
、α
ei
、β
ei
、γ
ei
为连杆在坐标系{ei}下受力的变形量。
[0032]
优选的，建立机器人的增强刚柔耦合运动学模型，表达式为：
[0033]
[0034]
其中：-1
t6为法兰坐标系{6}在设备基础坐标系{-1}下的齐次变换；it
ei
为连杆末端坐标系{ei}在连杆坐标系{i}下的齐次变换；为机器人的mdh运动学参数；κ代表连杆的柔性系数；q代表机器人各轴的坐标；f()为机器人的增强刚柔耦合模型前向运动学表达式。
[0035]
优选的，所述模块m4包括：建立标定模型，表达式为：
[0036][0037]
其中：
l
t-1
为设备基础坐标系{-1}在激光跟踪仪测量坐标系{l}下的齐次变换，ψ是对应位姿参数；i3为3阶单位矩阵；6t
tool
为工具坐标系{t}在法兰坐标系{6}下的齐次变换，τ为相对应的位姿参数；bj为跟踪仪测量靶球在工具坐标系下的坐标；h()为综合标定模型表达式；l表示第l个机器人位姿；j表示第j个靶球。
[0038]
优选的，将靶球固定到机器人末端上，利用跟踪仪测量机器人若干组关节坐标对应的靶球坐标推导用于levenberg
–
marquardt算法辨识的线性标定模型，表达式为：
[0039][0040]
其中：δq为偏差矢量；j
ξ
代表雅可比矩阵；δξ代表模型参数误差；为测量坐标和名义坐标的偏差；n为标定用的机器人位姿总数量。
[0041]
与现有技术相比，本发明具有如下的有益效果：
[0042]
(1)通过对机器人关节安装光栅尺系统，并实现全闭环控制，解决了标准工业机器人半闭环控制方式下的由于变形和反向间隙等问题引起的关节定位精度差的问题，达到了提高关节定位精度和机器人整体重复定位精度的效果；
[0043]
(2)通过增强的刚柔耦合模型和补偿算法，实现了工业机器人连杆重力变形和几何误差的补偿，大幅提升了机器人空间绝对定位精度。
附图说明
[0044]
通过阅读参照以下附图对非限制性实施例所作的详细描述，本发明的其它特征、目的和优点将会变得更明显：
[0045]
图1为机器人各个关节轴示意图；
[0046]
图2为机器人各连杆简化图；
[0047]
图3为机器人各连杆受力分析图；
[0048]
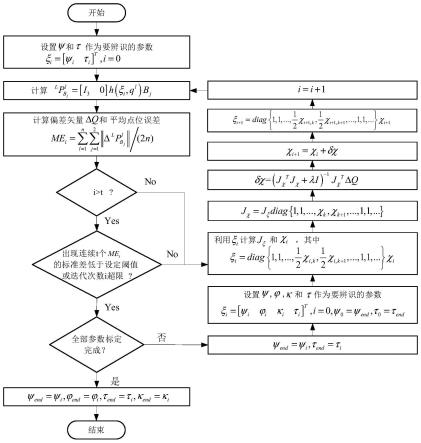
图4为两步levenberg
–
marquardt方法流程图；
[0049]
图5为机器人控制方法流程图；
[0050]
1.1-a1轴支架；1.2-a1轴读数头；1.3-a1轴光栅尺；2.1-a2轴支架；2.2-a2轴读数头；2.3-a2轴光栅尺；3.1-a3轴支架；3.2-a3轴读数头；3.3-a3轴光栅尺；4.1-a4轴支架；4.2-a4轴读数头；4.3-a4轴光栅尺；5.1-a5轴支架；5.2-a5轴读数头；5.3-a5轴光栅尺；6.1-a6轴支架；6.2-a6轴读数头；6.3-a6轴光栅尺。
具体实施方式
[0051]
下面结合具体实施例对本发明进行详细说明。以下实施例将有助于本领域的技术人员进一步理解本发明，但不以任何形式限制本发明。应当指出的是，对本领域的普通技术
人员来说，在不脱离本发明构思的前提下，还可以做出若干变化和改进。这些都属于本发明的保护范围。
[0052]
实施例1：
[0053]
本发明提供了一种基于关节全闭环和刚柔耦合模型的机器人精度提升方法，对标准工业机器人进行关节加光栅尺的全闭环改造，再结合增强刚柔耦合模型进行机器人绝对位置的补偿，实现机器人绝对定位精度的提升。
[0054]
如图1，在机器人各个关节轴的输出端增加光栅尺，形成关节的全闭环控制。其中光栅尺1.3、2.3、3.3、4.3、5.3、6.3分别贴在机器人各个关节的旋转表面上，读数头1.2、2.2、3.2、4.2、5.2、6.2分别通过支架1.1、2.1、3.1、4.1、5.1、6.1固定在机器人关节的固定端。通过读数头读取的光栅尺的刻度坐标，控制系统能够计算得到当前关节的旋转角度，进而以这种方式测量得到关节角度作为关节定位的基准。接着分别利用激光干涉仪对机器人的各个关节轴定位精度进行校准，之后利用激光跟踪仪对运动学模型参数进行校准，最终通过集成到控制系统中的补偿算法实现机器人绝对定位精度的大幅提升。
[0055]
具体实现步骤如下：
[0056]
(1)在机器人各关节安装光栅尺和读数头，将读数头的位置信号接入各轴电机的伺服控制器中，实现各个关节轴的全闭环控制；
[0057]
(2)利用激光干涉仪对机器人各关节定位精度进行校准；
[0058]
(3)建立机器人增强刚柔耦合运动学模型，具体为：
[0059]
首先将机器人各连杆简化为如图2所示连杆，在外力f、力矩m和自身重力mg的作用下，连杆末端坐标系{ei}的变形为：
[0060][0061]
其中：x
ei
、y
ei
、z
ei
、α
ei
、β
ei
、γ
ei
为连杆在坐标系{ei}下受力的变形量，如图3，具体如下：
[0062][0063]
其中，和为连杆的柔度系数。
[0064]
在此基础上，建立机器人的增强刚柔耦合运动学模型如下：
[0065][0066]
其中：-1
t6为法兰坐标系{6}在设备基础坐标系{-1}下的齐次变换；it
ei
为连杆末端坐标系{ei}在连杆坐标系{i}下的齐次变换；κ代表连杆的柔性系数，q代表机器人各轴的坐标；
[0067]
i-1
ti＝rot
x
(α
i-1
)trans
x
(a
i-1
)rotz(θi)transz(di)
[0068]2t3＝roty(β2)rot
x
(α2)trans
x
(a2)rotz(θ3)，其中α
i-1
，a
i-1
，θi，di为机器人的mdh运动学参数，用指代。
[0069]
(4)利用激光跟踪仪对机器人增强刚柔耦合模型参数进行校准。
[0070]
首先建立标定模型如下：
[0071][0072]
其中：
[0073]
1)
l
t-1
＝trans
x
(x-1
)transy(y-1
)transz(z-1
)rotz(α-1
)roty(β-1
)rot
x
(γ-1
)为设备基础坐标系{-1}在激光跟踪仪测量坐标系{l}下的齐次变换，x-1
,y-1
,z-1
,α-1
,β-1
,γ-1
是位姿参数，用ψ表示；
[0074]
2)6t
tool
＝trans
x
(x
t
)transy(y
t
)transz(z
t
)rotz(α
t
)roty(β
t
)rot
x
(γ
t
)为工具坐标系{t}在法兰坐标系{6}下的齐次变换，x
t
,y
t
,z
t
,α
t
,β
t
,γ
t
为相对应的位姿参数，用τ表示；
[0075]
3)为跟踪仪测量靶球在工具坐标系下的坐标；
[0076]
4)i3为3阶单位矩阵
[0077]
据此，推导出用于levenberg
–
marquardt方法辨识的线性标定模型如下：
[0078][0079]
其中，j
ξ
代表雅可比矩阵，δξ代表模型参数误差，为测量坐标和名义坐标的偏差；
[0080]
将靶球固定到机器人末端上，之后利用跟踪仪测量机器人在若干关节坐标系下的靶球坐标通过图4所示两步levenberg
–
marquardt(lm)方法，完成参数辨识：
[0081]
step1：首先设置ψ和τ作为粗辨识的参数ξi，标定模型的初始参数值采用名义值；
[0082]
step2：计算每组关节坐标对应的标定模型下的靶球坐标
[0083]
step3：根据激光跟踪仪实测的靶球坐标和模型下的靶球坐标计算偏差矢量δq和该模型参数ξi对应的平均点位误差
[0084]
step4：当出现连续t个mei的标准差低于设定阈值或迭代次数超过设定阈值后，如果当前处于粗辨识阶段则转至step8，如果当前已处于精辨识阶段则转至step9；否则，执行step5；
[0085]
step5：利用ξi计算辨识的雅克比矩阵j
ξ
和临时参数向量χi，其中临时参数向量用于约束最终辨识出来的参数取值范围，其和标定模型参数间存在如下关系：
[0086][0087]
其中，diag{}代表对角矩阵，χ
i,k
为χi中的第k个元素，对应于标定模型参数中的柔性参数。
[0088]
step6：计算临时雅克比矩阵j
χ
＝j
ξ
diag{1,1,...,χk,χ
k+1
,...,1,1,...}和临时参数向量的修正量：δχ＝(j
χtjχ
+λi)-1jχt
δq
[0089]
其中，λ为lm法的参数，i为单位矩阵。
[0090]
step7：计算修正后的临时参数向量χ
i+1
＝χi+δχ和标定模型参数；
[0091]
转入step2；
[0092]
step8：设置ψ，κ和τ作为要辨识的参数ξi，并将粗辨识最终得到的ψ和τ作为精辨识时的初始值，转至step5，开始精辨识。
[0093]
step9：将辨识得到的最后一次的ψ，κ和τ作为最终的辨识出的参数输出。
[0094]
(5)利用增强刚柔耦合模型对机器人定位实现补偿。
[0095]
如图5，将补偿算法集成到机器人控制系统中，从而实现机器人定位精度的最终补偿，步骤如下：
[0096]
step1：将编程位姿pos
p
赋值给名义位姿posn；
[0097]
step2：根据名义dh运动学模型逆解计算名义位姿posn对应的关节角度坐标q；
[0098]
step3：利用增强刚柔耦合模型计算q对应的正解位姿pos
t
；
[0099]
step4：计算位姿偏差δpos＝pos
p-pos
t
，如果偏差小于设定阈值，则转至step6，否则执行step4；
[0100]
step5：将偏差叠加至名义位姿pos
n(i+1)
＝pos
ni
+δpos，转至step2；
[0101]
step6：由于控制系统中的机器人参数采用名义dh运动学参数，故在控制系统中设定机器人定位至q或posn，可使得机器人最终实际定位位置逼近pos
p
。
[0102]
实施例2：
[0103]
本发明还提供一种基于关节全闭环和刚柔耦合模型的机器人精度提升系统，所述基于关节全闭环和刚柔耦合模型的机器人精度提升系统可以通过执行所述基于关节全闭环和刚柔耦合模型的机器人精度提升方法的流程步骤予以实现，即本领域技术人员可以将所述基于关节全闭环和刚柔耦合模型的机器人精度提升方法理解为所述基于关节全闭环和刚柔耦合模型的机器人精度提升系统的优选实施方式。
[0104]
根据本发明提供的基于关节全闭环和刚柔耦合模型的机器人精度提升系统，包括如下模块：模块m1：通过安装在机器人各关节的光栅尺和读数头，将读数头的位置信号接入各轴电机的伺服控制器中，实现各个关节轴的全闭环控制；模块m2：利用激光干涉仪对机器人各关节定位精度进行校准；模块m3：建立机器人增强刚柔耦合运动学模型；模块m4：利用激光跟踪仪对机器人增强刚柔耦合运动学模型参数进行校准；模块m5：利用增强刚柔耦合运动学模型对机器人定位进行补偿。
[0105]
所述模块m3包括：在外力f、力矩m和自身重力mg的作用下，连杆末端坐标系{ei}的变形为：
[0106][0107]
其中：x
ei
、y
ei
、z
ei
、α
ei
、β
ei
、γ
ei
为连杆在坐标系{ei}下受力的变形量。
[0108]
建立机器人的增强刚柔耦合运动学模型，表达式为：
[0109][0110]
其中：-1
t6为法兰坐标系{6}在设备基础坐标系{-1}下的齐次变换；it
ei
为连杆末端坐标系{ei}在连杆坐标系{i}下的齐次变换；为机器人的mdh运动学参数；κ代表连杆的柔性系数；q代表机器人各轴的坐标；f()为机器人的增强刚柔耦合模型前向运动学表达式。
[0111]
所述模块m4包括：建立标定模型，表达式为：
[0112][0113]
其中：
l
t-1
为设备基础坐标系{-1}在激光跟踪仪测量坐标系{l}下的齐次变换，ψ是对应位姿参数；i3为3阶单位矩阵；6t
tool
为工具坐标系{t}在法兰坐标系{6}下的齐次变换，τ为相对应的位姿参数；bj为跟踪仪测量靶球在工具坐标系下的坐标；h()为综合标定模型表达式；l表示第l个机器人位姿；j表示第j个靶球。
[0114]
将靶球固定到机器人末端上，利用跟踪仪测量机器人若干组关节坐标对应的靶球坐标推导用于levenberg
–
marquardt算法辨识的线性标定模型，表达式为：
[0115][0116]
其中：δq为偏差矢量；j
ξ
代表雅可比矩阵；δξ代表模型参数误差；为测量坐标和名义坐标的偏差；n为标定用的机器人位姿总数量。
[0117]
在本技术的描述中，需要理解的是，术语“上”、“下”、“前”、“后”、“左”、“右”、“竖直”、“水平”、“顶”、“底”、“内”、“外”等指示的方位或位置关系为基于附图所示的方位或位置关系，仅是为了便于描述本技术和简化描述，而不是指示或暗示所指的装置或元件必须具有特定的方位、以特定的方位构造和操作，因此不能理解为对本技术的限制。
[0118]
本领域技术人员知道，除了以纯计算机可读程序代码方式实现本发明提供的系统、装置及其各个模块以外，完全可以通过将方法步骤进行逻辑编程来使得本发明提供的系统、装置及其各个模块以逻辑门、开关、专用集成电路、可编程逻辑控制器以及嵌入式微控制器等的形式来实现相同程序。所以，本发明提供的系统、装置及其各个模块可以被认为是一种硬件部件，而对其内包括的用于实现各种程序的模块也可以视为硬件部件内的结构；也可以将用于实现各种功能的模块视为既可以是实现方法的软件程序又可以是硬件部件内的结构。
[0119]
以上对本发明的具体实施例进行了描述。需要理解的是，本发明并不局限于上述特定实施方式，本领域技术人员可以在权利要求的范围内做出各种变化或修改，这并不影响本发明的实质内容。在不冲突的情况下，本技术的实施例和实施例中的特征可以任意相
互组合。