一种基于数据驱动的水下机械臂抗扰预测控制方法

本发明涉及串联机械臂控制，尤其涉及一种基于数据驱动的水下机械臂抗扰预测控制方法。

背景技术：

1、随着国家发展和社会进步，人们对资源的需求也愈发强烈。但由于对陆地资源的过度开发，导致地面上可利用的资源逐渐减少，于是就将目光投向了海洋。机械臂被认为是执行海底干预操作的最合适工具，由于水下机械臂的作业范围、动力特性以及作业的自主性、可靠性、准确性和灵活性等关系着整个水下机器人系统的作业能力，因此研究水下机械臂及其相关运动控制技术愈发重要。

2、目前，针对水下机械臂运动控制，主要采用的方法有：自适应控制、滑模控制、神经网络控制等，但是这些控制方法对于机械臂模型的依赖程度高，抗扰能力不强，且控制器设计较为复杂，给系统调试带来较大的困难。自抗扰控制是一种不依赖于模型的鲁棒控制方法，具有结构简单、抗扰能力强等优点，在水下机械臂控制领域具有良好的应用前景。自抗扰控制通过eso来估计扰动，当系统存在噪声时，eso带宽受限，从而影响最终控制效果。

3、如何解决上述技术问题为本发明面临的课题。

技术实现思路

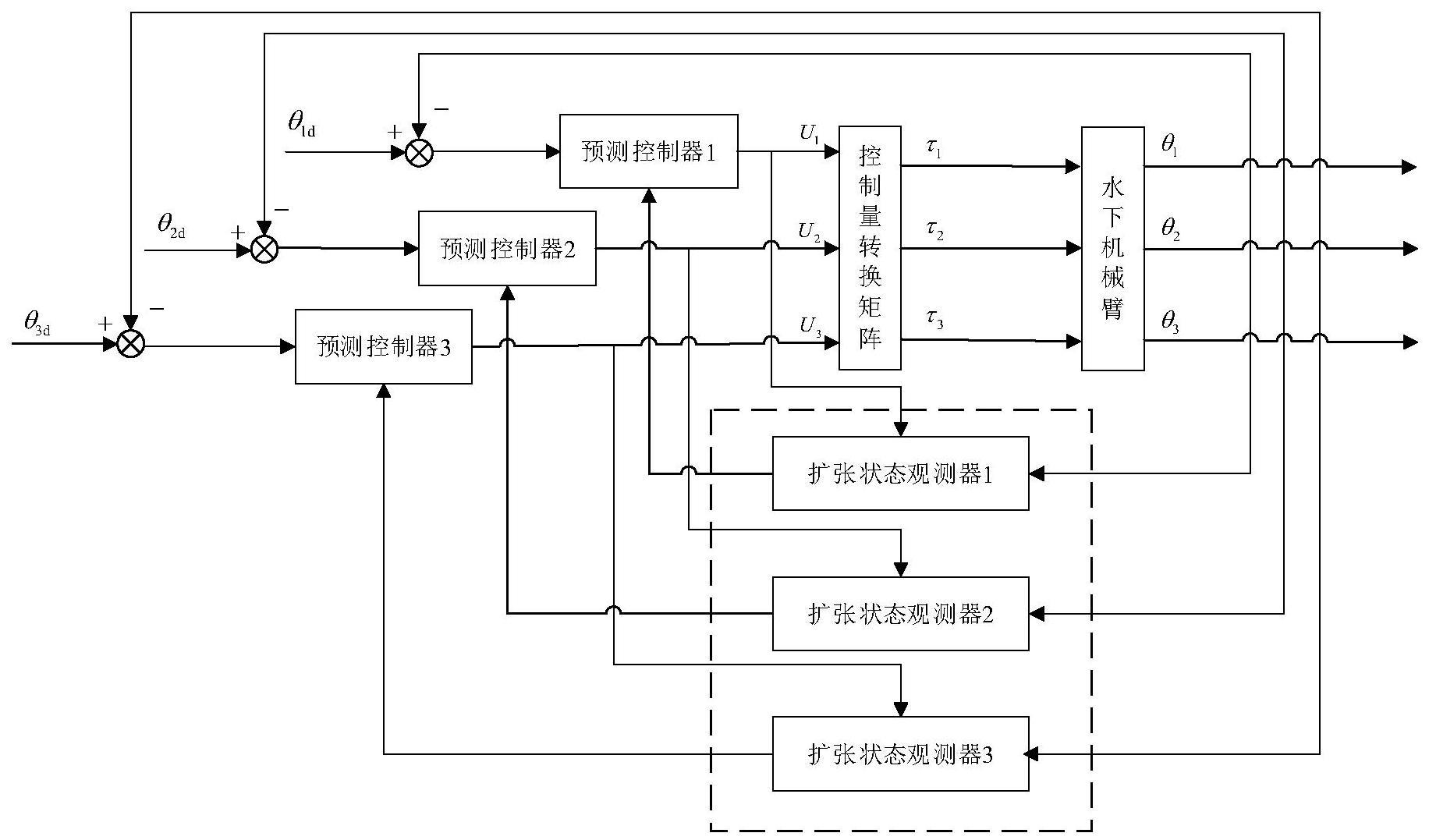
1、本发明的目的在于提供一种基于数据驱动的水下机械臂抗扰预测控制方法，由于水下机械臂系统具有非线性、强耦合性和扰动多等特点，系统模型无法精确建立，因此设计eso对系统的不确定性进行观测并补偿，以减弱不确定性和水下扰动对关节控制精度的影响。对补偿后的标准串联结构采用预测控制，增强控制器鲁棒性，使得水下机械臂具有良好的自适应能力、抗干扰能力及鲁棒稳定性。

2、本发明的发明思想为：本发明考虑将自抗扰控制中的pd控制器改进为预测控制器，利用预测控制器滚动优化的特点，增强系统的鲁棒性，将预测控制与自抗扰控制相结合，实现两种控制方法优势互补，利用eso估计扰动并补偿，将系统等效为串联积分器，此时预测控制方法中的预测模型无需在线辨识，从而降低控制器设计的复杂性，实现利用数据驱动方式设计预测控制器，所提出方法具有抗扰能力强和鲁棒性强的特点，在水下机械臂控制中有较好控制效果。

3、为了实现上述发明目的，本发明采用技术方案具体为：一种基于数据驱动的水下机械臂抗扰预测控制方法，包括以下步骤：

4、步骤s1：建立三关节水下机械臂动力学模型。

5、首先分析陆上环境不考虑水阻等因素，根据lagrange方程法建立水下机械臂的常规动力学模型，拉格朗日函数l为系统总动能和总势能之差，具体如下：

6、l＝k-p   (1)

7、其中，k为机械臂系统的总动能，p为机械臂系统的总势能。

8、对式(1)中每一项进行求导，可以得到lagrange方程，具体如下：

9、

10、其中，θi和分别是机械臂关节i的关节角度和关节角速度，τi是使机械臂关节i运动的力矩。

11、通过计算每个质点的速度和加速度等，得到系统的动能和势能，通过式(2)的拉格朗日函数推导动力学方程，具体如下：

12、

13、其中，θ＝[θ1 θ2 θ3]t，θ、和分别代表了机械臂的关节角度、关节速度和关节加速度，是关于时间t的函数；m(θ)是机械臂的3×3阶质量矩阵，是3×1阶的离心力和哥氏力矢量矩阵，g(θ)是3×1阶的等效重力矢量矩阵，τ为机械臂关节的力矩。

14、水下机械臂在水下环境作业时会受到水的作用力，主要包括水阻力和附加质量力等，可以通过基于流体力学的morison经验公式求得水动力矩，具体如下：

15、

16、其中，ρ为水密度，cd为水阻力系数，cm为附加质量力系数，l为机械臂连杆长度，为机械臂连杆表面的法向速度分量，d为机械臂连杆的等效直径。

17、将式(4)中的水动力矩代入式(3)机械臂的常规动力学方程中，得到水下机械臂动力学模型，具体如下：

18、

19、其中，表示水动力作用产生的合力矩。

20、步骤s2：考虑关节运动以及在流体中旋转的转子会受到粘性摩擦阻力，将所述三关节水下机械臂动力学模型转化成二阶系统的形式。

21、进一步地，步骤s2中，考虑到以电机作为关节执行装置的机械臂，用适当的数学模型描述其关节的运动以及在流体中旋转的转子会受到粘性摩擦阻力。为了对水下机械臂进行轨迹跟踪，将式(5)的动力学模型转化成二阶系统的形式，具体如下：

22、

23、其中，j是电机的转动惯量，是粘性摩擦阻力矩，通过实验测得。

24、步骤s3：针对所述三关节水下机械臂动力学模型中的不确定性参数和外部扰动难以精确测量的问题，简化二阶系统表达式。

25、进一步地，步骤s3中，简化式(6)中的二阶系统表达式，具体如下：

26、

27、其中，u＝[u1 u2 u3]t，f＝[f1 f2 f3]t，u＝(m(θ)+j)-1τ为虚拟控制量，为系统总扰动影响，(m(θ)+j)-1为控制量转换矩阵。

28、步骤s4：针对简化后的综合扰动，设计降阶扩张观测器，将系统转化成标准的串联积分器的形式。

29、进一步地，步骤s4中，针对式(7)中的θi，i＝1,2,3，设计降阶扩张观测器(extended state observer，eso)，具体如下：

30、

31、其中，z＝[z2 z3]t为观测系统状态的观测量，z2为的观测值，z3为fi的观测值，β1和β2分别为降阶eso的增益。

32、设w1＝z2-β1θi，w2＝z3-β2θi，式(8)可改写为：

33、

34、由式(9)可求得降阶eso的输出量w2，进一步利用如下公式求得fi的观测值z3：

35、z3＝w2+β2θi   (10)

36、步骤s5：针对所述降阶eso估计并补偿后的系统设计数据驱动的抗扰预测控制器。

37、进一步地，步骤s5中，首先针对θi回路，i＝1,2,3，具体如下：

38、ui＝u0i-z3   (11)

39、其中，u0i为所述数据驱动的抗扰预测控制器的控制律。

40、其次，针对所述降阶eso估计并补偿后的系统采用受控自回归积分滑动平均模型(controlled auto regression and moving average model，carma)作为预测模型，具体如下：

41、a(z-1)θii(k)＝b(z-1)u0i(k-1)+c(z-1)ζ(k)   (12)

42、其中，u0i(k)和θi(k)为k时刻输入输出的采样信号，z-1为后移算子，ζ(k)为扰动信号，a(z-1)、b(z-1)和c(z-1)为后移算子的多项式，系数a(z-1)为首一多项式，系数b(z-1)的若干首项元素可以为零，表示系统所受时滞的影响，系数c(z-1)为随机干扰的系数。a(z-1)、b(z-1)和c(z-1)取值形式如下：

43、

44、引入丢番图方程，具体如下：

45、

46、其中，ej(z-1)、fj(z-1)、gj(z-1)和hj(z-1)均为丢番图多项式系数，j＝1,2,...,n，具体如下：

47、

48、其中，ek和gk分别为ej(z-1)和gj(z-1)多项式的系数，k＝1,2,...,j；和分别为fj(z-1)和hj(z-1)的多项式系数，m＝1,2,...,n-1，n＝1,2,...,n。

49、将式(12)和式(13)代入到式(14)和式(15)，得到二阶丢番图方程通解，具体形式如下：

50、

51、系统的输出预测值具体形式如下：

52、θi＝gu0i+fθi(k)+hu0i(k-1)   (17)

53、其中，

54、θi＝[θi(k+1),…,θi(k+n)]t；

55、u0i＝[u0i(k),…,u0i(k+nu-1)]t；

56、f＝[f1,…,fn]t；

57、h＝ph1,…,hn]t；

58、

59、在预测控制中，通过一个性能指标来控制系统的优化，具体如下：

60、

61、其中，θi(k+j)为对输出的预测序列，u0i(k+j)为将来的控制序列，n为预测时域，nu为控制时域，λ为控制加权因子，λ＞0，u0i(k+j)＝0表示在nu步后控制量不在变化，j＝nu,...,n，v(k+j)为设定值的柔化序列，使得输出θi(k)可以平稳达到设定值θid(k)，具体如下：

62、

63、其中，α为柔化因子，0≤α＜1，fα＝[α,…,αn]t，

64、将式(18)中的性能指标改写为向量形式，具体如下：

65、j＝(θi-v)t(θi-v)+λu0itu0i   (20)

66、对性能指标进行求极值运算，得到性能指标j取得最小值时的控制律，具体如下：

67、u0i＝(gtg+λi)-1gt[v-fθi(k)-hu0i(k-1)]   (21)

68、将式(21)中的第1个元素作为控制量u0i(k)，具体如下：

69、

70、其中，ht＝[1 0 … 0](gtg+λi)-1gt。

71、将式(19)代入式(22)，求得：

72、

73、步骤s6：根据系统预设性能指标，采用定量反馈理论对数据驱动的抗扰预测控制器中的参数β1，β2，n，nu，λ，α，t进行整定。根据控制量转换矩阵，求解作用在电机的三个关节的力矩，传入机械臂各关节的电机控制系统进而实现机械臂各关节角度的跟踪控制。

74、进一步地，步骤6中，对数据驱动的抗扰预测控制器进行参数整定，具体如下：

75、合理选择自抗扰扩张状态观测器的参数β1和β2，使系统动态性能指标达到最优；采用定量反馈理论，结合系统性能指标合理选择预测控制器的预测时域n、控制时域nu、控制加权因子λ、柔化因子α以及采样周期t，得到最优控制律u，再根据τ＝(m(θ)+j)u得到实际作用于电机的控制力矩。

76、与现有技术相比，本发明的有益效果为：

77、(1)本发明的控制方法对于机械臂动力学模型精度要求低，允许模型存在一定偏差，方法具有较强的鲁棒性。同时针对机械臂动力学的耦合特性和水下阻力，通过eso实现耦合与水下阻力干扰的实时观测，设计解耦补偿控制方案，因此控制方法具有较强的解耦能力与抗干扰能力；

78、(2)针对噪声环境下eso带宽受限问题，采用数据驱动方式设计预测控制器，借助预测控制滚动优化的特点，增强控制方法的鲁棒性。与传统adrc相比，本发明的控制方法可以在传感器存在测量噪声环境下具有更好的动态性能和鲁棒稳定性。

79、(3)本发明结合水下机械臂动力学理论、自抗扰控制技术和预测控制技术实现的水下机械臂控制方法。针对参数不确定的水下机械臂采用降阶扩张状态观测器对系统不确定性和扰动进行了估计和补偿，将转变后的串联积分系统设计预测控制器获得最优控制律，实现水下机械臂的轨迹跟踪控制。