基于无模型强化学习的漂浮基空间机械臂末端位置控制方法

本发明属于空间机械臂控制领域，具体涉及一种基于无模型强化学习的漂浮基空间机械臂末端位置控制方法。

背景技术：

1、空间机械臂被越来越广泛地应用于空间任务中。而漂浮基座的空间机械臂因其节省燃料、操作灵活、碰撞损失小等特点在空间任务中具有独特的优势。不同于基座受控的空间机械臂，漂浮基座空间机械臂的基座和机械臂之间存在很强的动力学耦合，机械臂的运动会引起基座位置和姿态的变化，这使得它具有和固定基座机械臂不同的运动学和动力学特性，从而使得传统的机械臂建模与控制方法无法直接用于漂浮基机械臂。此外，由于燃料消耗、动力学部件参数误差等问题，建立漂浮基机械臂的精确动力学模型也并不容易。无模型强化学习作为一种完全基于数据的算法，采用智能体与环境交互获取数据，并在此基础上进行优化得到控制器。使用无模型强化学习进行空间机械臂的控制，避免了复杂的运动学和动力学建模过程，针对传统控制方法具有独特的优越性。但是现有的无模型强化学习对训练参数和训练环境十分敏感，造成基于现有的无模型强化学习算法得到的控制器缺乏稳定性和泛化性能，使得算法性能在环境变化(如系统参数变化，受到外部扰动)的条件下通常会有所下降。此外，由无模型强化学习训练得到的算法无法进行理论上的稳定性证明，这使得算法部署于其上的系统存在安全隐患。

2、综上所述，基于现有的无模型强化学习算法得到的控制器缺乏鲁棒性和稳定性，且现有的无模型强化学习算法无法进行理论上的稳定性证明，因此，极大地限制了无模型强化学习在空间机械臂控制领域的应用。

技术实现思路

1、本发明的目的是为解决基于现有的无模型强化学习算法得到的控制器缺乏鲁棒性和稳定性的问题，而提出的一种基于无模型强化学习的漂浮基空间机械臂末端位置控制方法。

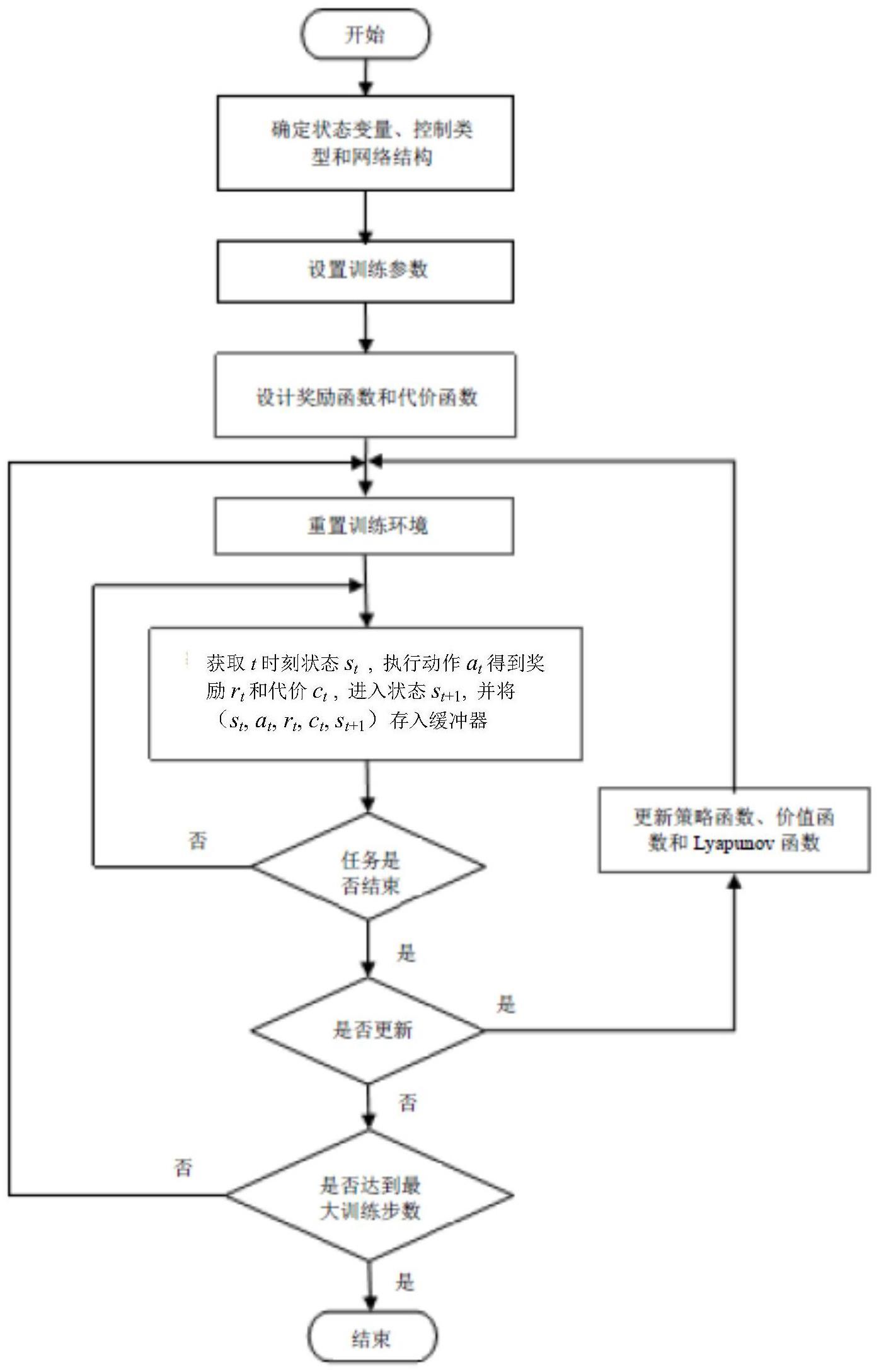
2、本发明为解决上述技术问题所采取的技术方案是：一种基于无模型强化学习的漂浮基空间机械臂末端位置控制方法，所述方法具体包括以下步骤：

3、步骤一、确定漂浮基空间机械臂系统的输入状态变量和控制输出类型；

4、步骤二、根据空间机械臂的动作空间维度确定控制策略函数πθ、价值函数qφ和lyapunov函数lψ的网络结构，θ是控制策略函数的网络参数，φ是价值函数的网络参数，ψ是lyapunov函数的网络参数；

5、所述控制策略函数、价值函数和lyapunov函数都由mlp神经网络表示；

6、步骤三、设计奖励函数和lyapunov代价函数；

7、步骤四、设置总训练步数、每一幕(episode)的长度(幕是指任务从开始到结束的过程，空间机械臂从初始位置开始向目标位置运动，到达一幕的最大步数后这一幕即结束；长度指每一幕包含的步数)、策略更新时batch的大小、缓冲器的容量以及策略更新频率；

8、步骤五、初始化控制策略函数πθ、价值函数qφ和lyapunov函数lψ的网络参数，并设置目标价值函数将目标价值函数的网络参数初始化为价值函数qφ的网络参数；

9、步骤六、对环境进行重置，将空间机械臂系统置为初始状态，并设置目标位置；

10、步骤七、从环境中获取当前状态st后，将获取的当前状态st输入控制策略函数πθ，空间机械臂执行控制策略函数πθ输出的动作at并进入下一个状态st+1；

11、将元组(st,at,rt,ct,st+1)存入缓冲器，其中，rt是空间机械臂在当前状态st执行动作at获得的奖励，ct是空间机械臂在当前状态st执行动作at获得的lyapunov代价；将空间机械臂每执行一次动作并进入下一状态定义为一步；

12、步骤八、判断当前幕的任务是否结束，即判断步数是否达到当前幕的长度；

13、若当前幕的任务未结束，则利用状态st+1返回步骤七；

14、否则，当前幕的任务结束，则判断是否达到策略更新频率；

15、若达到策略更新频率，则从缓冲器中采样一个batch的元组更新控制策略函数πθ、价值函数qφ和lyapunov函数lψ的网络参数，并将更新后的价值函数qφ网络参数复制到目标价值函数再返回步骤六；

16、否则未达到策略更新频率，则执行步骤九；

17、步骤九、判断是否达到设置的总训练步数，若达到设置的总训练步数，则结束训练并执行步骤十，否则未达到设置的总训练步数，则返回步骤六；

18、步骤十、将结束训练时获得的控制策略函数的网络参数作为训练好的网络参数，根据训练好的网络参数对漂浮基空间机械臂系统进行实时控制。

19、进一步地，所述漂浮基空间机械臂系统的输入状态变量中包含的信息有基座位置pb、基座姿态ob、空间机械臂关节位置q、关节角速度和目标位置pt。

20、对于漂浮基空间机械臂系统的位置控制任务，输入状态变量中必须包含上述信息，为了提升算法效果，也可以进一步加入机械臂末端执行器位置以及当前末端位置误差等信息。

21、进一步地，所述漂浮基空间机械臂系统的控制输出类型为关节角速度或关节力矩。

22、进一步地，所述奖励函数设计为：

23、

24、其中，r表示奖励函数，pt表示目标位置向量，pe表示空间机械臂末端位置向量，||·||2表示2范数。

25、进一步地，所述lyapunov代价函数为：

26、c＝||pt-pe||2                    (2)

27、其中，c表示lyapunov代价函数。

28、进一步地，所述更新控制策略函数πθ、价值函数qφ和lyapunov函数lψ的网络参数，其具体的更新过程为：

29、对控制策略函数πθ的参数更新是完成式(3)的优化问题：

30、

31、其中，πθ(st)表示将状态st输入控制策略函数πθ输出的动作，qφ(st,πθ(st))表示控制策略函数πθ下的状态价值函数，p(st+1|st,πθ(st))表示在状态st执行动作πθ(st)后进入状态st+1的概率，lψ(·)代表lyapunov函数值，lψ(st)表示状态st处的lyapunov函数值，α为缩放系数，α＞0，fc是正定的lyapunov损失函数；

32、采用lagrange法得到式(3)的优化问题的对偶问题：

33、

34、其中，λ是lagrange乘子，lψ(st+1)表示状态st+1处的lyapunov函数值，j是待优化的目标函数；

35、通过随机梯度下降对式(4)进行优化，式(4)的梯度为：

36、

37、其中，表示j的梯度，表示控制策略函数πθ的梯度，πθ(at|st)表示控制策略函数πθ在状态st下输出动作at，表示控制策略函数πθ下的数学期望，表示控制策略函数πθ和状态空间下的数学期望；

38、控制策略函数πθ的参数通过式(6)更新：

39、

40、其中，δ是控制策略函数的网络参数更新时的学习率；

41、完成控制策略函数的参数更新后拟合价值函数qφ，价值函数的拟合等价于：

42、

43、其中，yt表示价值函数的目标值，qφ(st,at)表示在状态st执行动作at的价值，表示状态空间下的数学期望，jq表示价值函数拟合时的损失函数；

44、yt由目标价值函数经自举法导出：

45、

46、其中，πθ(at+1|st+1)表示策略πθ在状态st+1下输出动作at+1，γ表示累积奖励的折扣率，表示目标价值函数在状态st+1和动作at+1下的输出；

47、价值函数qφ的网络参数通过式(9)更新：

48、

49、其中，表示jq的梯度，δ′是价值函数的网络参数更新时的学习率；

50、lyapunov函数lψ的网络参数更新等价于式(10)：

51、

52、其中，lψ(st)表示在状态st的lyapunov函数值，是通过采样得到的状态st下lyapunov函数的无偏估，jl是lyapunov函数拟合时的损失函数；

53、

54、其中，fc(st)表示st状态下正定lyapunov损失函数，t表示每一幕的长度；

55、lyapunov函数的网络参数通过式(12)更新：

56、

57、其中，表示jl的梯度。

58、进一步地，所述lagrange乘子的更新方式为：

59、

60、其中，jλ表示lagrange乘子更新时的损失函数；

61、lagrange乘子通过式(14)更新：

62、

63、其中，表示jλ的梯度。

64、进一步地，所述正定的lyapunov损失函数fc为：

65、

66、其中，se是漂浮基空间机械臂系统的目标状态，表示控制策略函数πθ下的数学期望。

67、进一步地，所述控制策略函数和lyapunov函数的学习率均为0.0003，价值函数的学习率为0.001。

68、更进一步地，所述缓冲器的容量不小于策略更新时batch的3倍，若达到缓冲器容量限制，则删除当前缓冲器中最早存储的元组，将新元组保存到缓冲器中。

69、本发明的有益效果是：

70、1、本发明采用无模型强化学习进行漂浮基空间机械臂的定位控制，直接通过系统状态量的输入生成控制策略，避免了漂浮基空间机械臂建模复杂且存在模型误差的问题。且本发明方法相较于传统控制方案更具有普适性，可直接用于各种不同构型的空间机械臂，无需重复进行控制器设计。

71、2、本发明将lyapunov方法引入强化学习，使得通过强化学习得到的算法具有了稳定性保障，提升了算法对环境参数变化和外部扰动的鲁棒性。实验表明本发明方法在面对系统动力学参数变化和外部力矩干扰时，依然可以实现高精度的位置控制，其鲁棒性超过了当前主流的无模型强化学习算法。

72、3、本发明提出了一种基于采样的lyapunov稳定性条件，从而可以在无需系统模型的条件下通过lyapunov方法对系统稳定性进行判断，籍此在无模型优化过程中加入对策略稳定性的约束。

73、4、本发明采用了独立于价值函数、奖励函数的lyapunov函数和lyapunov代价函数，相较于现有的安全强化学习用lyapunov函数作为价值函数的方法，本发明避免了因lyapunov函数正定性而导致的强化学习策略对动作空间的探索受限以及更新效率下降的问题。