一种高阶滑膜动量观测器来估计机械臂外力的方法

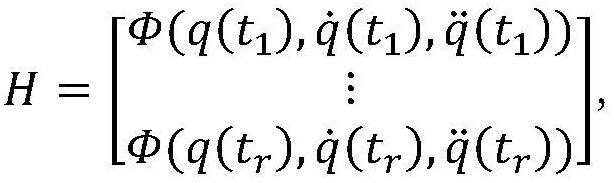
本发明涉及一种高阶滑膜动量观测器来估计机械臂外力的方法。

背景技术：

1、随着机械臂在各个领域的广泛应用，如打磨、装配、医疗服务等应用场景日趋复杂化和多样化，机械臂不可避免的要在非构环境下工作，成为工人的“同事”，和工人共享工作空间，协助完成工作任务。在这些应用中要求机械臂具有一个重要的共同特征，即具有力感知能力，因此需要对机械臂的外力进行估计。

2、另外，机械臂所受到摩擦力的非线性影响也会严重限制外力估计的精度，尤其在低速情况下这种非线性影响更加显著，并且摩擦力在动力学模型中占主导作用，此时的摩擦力模型非常复杂。因此，在对机械臂的外力进行估算时，还需要考虑这部分因素。

技术实现思路

1、本发明的主要目的是提供一种高阶滑膜动量观测器来估计机械臂外力的方法，来实现对机械臂外力的精确估计。

2、为了实现上述主要目的，本发明提供了一种高阶滑膜动量观测器来估计机械臂外力的方法，其包括以下步骤：

3、s1)建立机械臂的动力学模型

4、机械臂的动力学模型表示如下：

5、

6、τm＝kri (1-2)

7、其中，m(q)∈rn×n为机械臂对称的正定惯量矩阵，为科氏力和离心力，g(q)∈rn为重力，τm∈rn关节驱动力矩，τext∈rn为关节受到外力矩，τf∈rn为不确定性的扰动力矩，q∈rn为关节位移,n为机械臂自由度数，k为电机常数，r为传动比，i为关节电流；动力学模型具有以下性质：

8、①为斜对称矩阵，并满足：

9、

10、②公式(1)的左边可以线性化为：

11、

12、其中，为回归矩阵，p∈rn×1为机械臂的动力学参数；

13、s2)动力学参数的辨识

14、通过机械臂激励实验中测量得到的数据，利用公式(1-4)的动力学线性化模型对机械臂动力学参数进行辨识；通过激励轨迹用来持续的激励机械臂系统，使机械臂按照指定的激励轨迹运行，采集关节位的位置和电流，得到超定方程组：

15、γ＝hp (2-1)

16、其中，γ＝[τ(t1)t … τ(tr)t]；观测矩阵tr为采集时刻；

17、机械臂的动力学参数采用最小二乘法求得：

18、

19、其中，h+＝(hth)-1ht,为机械臂动力学参数估计值；

20、s3)利用神经网络对关节摩擦力进行动态补偿

21、基于库伦和粘滞摩擦力模型并借助具有良好非线性逼近能力的神经网络，建立自适应参数调节的摩擦力补偿模型公式如下：

22、

23、其中，δτf为未建模的非线性项，分别为借助神经网络动态调整的库伦摩擦力系数和粘滞摩擦力系数；

24、s4)建立高阶滑膜动量观测器来观测机械臂所承受的交互力

25、通过结合动力学性质和动力学参数辨识的结果来求解观测器所需的参数；具体如下：

26、

27、

28、μi＝[0,…,1,…,0]t

29、

30、mi为m的第i列，cij为c中元素，结合公式(1-3)和(4-3)便可求得

31、所建立高阶滑膜动量观测器可表示为：

32、

33、其中，

34、根据本发明的一种具体实施方式，在步骤s2中，采用包含不同频率sine和cosine函数的5次傅立叶级数激励轨迹，其中，机械臂第k个关节的期望激励轨迹表示如下：

35、

36、其中，wf为基础频率，和为sine和cosine函数振幅，qk0表示轨迹偏移；每个机械臂关节含有11个参数，关节的参数集成为向量β∈r11n。

37、根据本发明的一种具体实施方式，在步骤s2中，公式(2-3)对模型误差和噪声的敏感性取决于矩阵h的条件数，将激励轨迹的获取可看作是约束条件下的优化，即：

38、min cond(h) (2-4)

39、满足：

40、

41、公式(2-5)限制了关节位置、速度和加速度的运动范围，并设置期望的初始终止速度和加速度为零。

42、根据本发明的一种具体实施方式，在步骤s3中，神经网络采用三层感知基，由分别含有个神经元的输入层、隐藏层和输出层组成；神经网络代表输入层到输出层的非线性映射关系可表示为：

43、

44、其中，uij和vjk分别为第一层和第二层权重，φj为激励函数，xk为第k个输入，yi表示第i个输出，vj0和wi0为第一层和第二层的基础权重；

45、其中，机械臂关节速度作为输入，输出为和δτf的估计值，因此是在真实物理的实验中通过不断的试错确定的；

46、基于神经网络的摩擦力补偿算法中将公式(3-2)改写成矩阵的形式：

47、

48、u＝[u1,u2,u3] (3-4)

49、

50、其中，选择sigmoid函数作为激活函数：

51、φj(z)＝1/(1+e-z) (3-6)

52、神经网络中权重是通过最小化代价函数来确定：

53、

54、其中，p为采样个数，和分别为摩擦力的测量值和估计值。

55、根据本发明的一种具体实施方式，在步骤s4中机械臂的广义动量定义如下：

56、

57、公式(4-5)的微分形式如下：

58、

59、将公式(1-1)和(1-3)带入公式(4-6)可得：

60、

61、根据公式(4-7)，动量观测器定义为：

62、

63、其中，为的估计值，r为残余向量，k为正定对角增益矩阵；

64、将公式(4-7)带入(7-8)可得外力τext与r之间的关系为：

65、

66、对公式(4-9)两端拉普拉斯变换可得：

67、

68、其中，ri，τext,i和ki为r，τext和k的第i个元素；

69、在理想的条件下，由公式(4-10)可得：

70、

71、表明，实际应用过程中的ki要尽可能的选择较大的值。

72、进一步地，为使得观测器(4-4)一致稳定收敛，在步骤s4中增益εi(i＝1,2,3)的选择设置为基于高阶滑膜控制的扰动边界l,α>0选择足够小；

73、增益∈i的选择使得矩阵为赫尔维茨矩阵，函数θ定义为：

74、

75、其中，tu>0的值为随机选择；

76、定义结合公式(4-7)和(4-4)，可以得到观测误差方程为：

77、

78、误差方程可用通用的形式表示如下：

79、

80、ei,(i＝1,2,3)为增益系数，并假设存在且有界。

81、本发明具备以下有益效果：

82、本发明利用神经网络对关节摩擦力进行动态补偿，可有效消除外力估计过程中摩擦力的影响，基于高阶滑膜控制来估计机械臂的外力具有较高的精确性，同时还具有较强的抗噪能力。

83、为了更清楚地说明本发明的目的、技术方案和优点，下面结合附图和具体实施方式对本发明作进一步的详细说明。