一种智能装卸机械臂视觉避障轨迹控制方法与流程

本发明涉及视觉避障，特别涉及一种智能装卸机械臂视觉避障轨迹控制方法。

背景技术：

1、随着工业自动化的发展，智能装卸机械臂凭借其高效、精准和安全的特点，在物流、制造、仓储等领域中扮演着重要角色。然而，在复杂环境下，机械臂容易与障碍物发生碰撞冲突，导致安全风险和损失。为了提高机械臂的操作效率和安全性，各种方法被应用于智能装卸机械臂避障轨迹的控制。

2、谢春丽等人在《改进时间弹性带的动态避障轨迹规划系统研究》中首先模拟机械臂运行真实动态环境，采用均值滤波器对动态障碍物展开检测，然后建立代价地图层，实现障碍物聚类，并通过卡尔曼滤波对动态障碍物展开行动预测与定位，最后结合智能装卸机械臂的行动状态完成避障轨迹规划控制。但在动态环境下，障碍物的位置和形状可能会频繁变化，而障碍物聚类可能会受到多个障碍物相互重叠的影响，导致聚类结果不准确或不稳定，影响最终控制效果。马东阳等人在《基于改进粒子群算法的避障轨迹规划》中首先建立机械臂轨迹控制的多项式函数，并对其参数值展开优化，完成轨迹更新，然后将智能装卸机械臂的移动时间最短与关节转角增量最少设为优化目标，通过罚函数建立避障约束条件，以此将机械臂避障轨迹控制问题转化为对最优参数的求解问题，最后利用优化后的粒子群算法展开参数寻优，实现机械臂避障轨迹控制。此方法在实现过程中未充分考虑机械臂在运动过程中移动速度不均匀和不连续性的问题，难以确保操作的稳定性，这对于环境的实时变化和姿态不准确的情况会导致刚方法的控制性能下降。okan m等人在《tightmaneuvering for path planning of hyper-redundant manipulators in three-dimensional environments》中提出了一种基于几何方法的三维环境下有效路径规划算法，首先将机械臂的连杆与路径点相切，确保机械臂在移动过程中不会与周围的物体发生碰撞，然后采用一种各机械臂连杆之间没有交互的控制策略，保持每个连杆的关节在都保持在同一路径上，直到末端执行器达到目标位置，以此实现轨迹规划。此方法缺乏对连杆之间协同运动的考虑，导致在实现过程中出现运动不匀速的情况，无法有效避免碰撞冲突。lopes a m等人在《path planning ofa 5-dofrobotic arm based on birrt-apfalgorithm considering obstacle avoidance》中提出了基于人工势场法和双向快速探索随机树(birrt-apf)算法相结合的机械臂路径规划方法。首先根据bi-rrt算法的随机树双向增长特性优化吸引力函数，减少机械臂轨迹控制的时间，然后采用一种路径构建策略，剔除规划路径中的冗余节点，提高路径平滑性，最后采用人工势场法完成机械臂避障轨迹控制。此方法运用了人工势场法，在复杂环境中势场可能导致机械臂陷入局部最小值，估计控制精度和准确性会受到限制。总而言之，现有技术中，面对较复杂工况环境，智能装卸机械臂无法有效规避障碍物。

3、鉴于此，需要一种智能装卸机械臂视觉避障轨迹控制方法。

技术实现思路

1、针对现有技术中面对较复杂工况环境，智能装卸机械臂无法有效规避障碍物的问题，本发明提供了一种智能装卸机械臂视觉避障轨迹控制方法，能够采用混合插值样条对轨迹控制进行优化处理，在轨迹路径最大曲率约束条件下，提高轨迹控制的连续性，从而提高了轨迹的平滑度，缩短了其避障路径长度。具体技术方案如下：

2、一种智能装卸机械臂视觉避障轨迹控制方法，包括以下步骤：

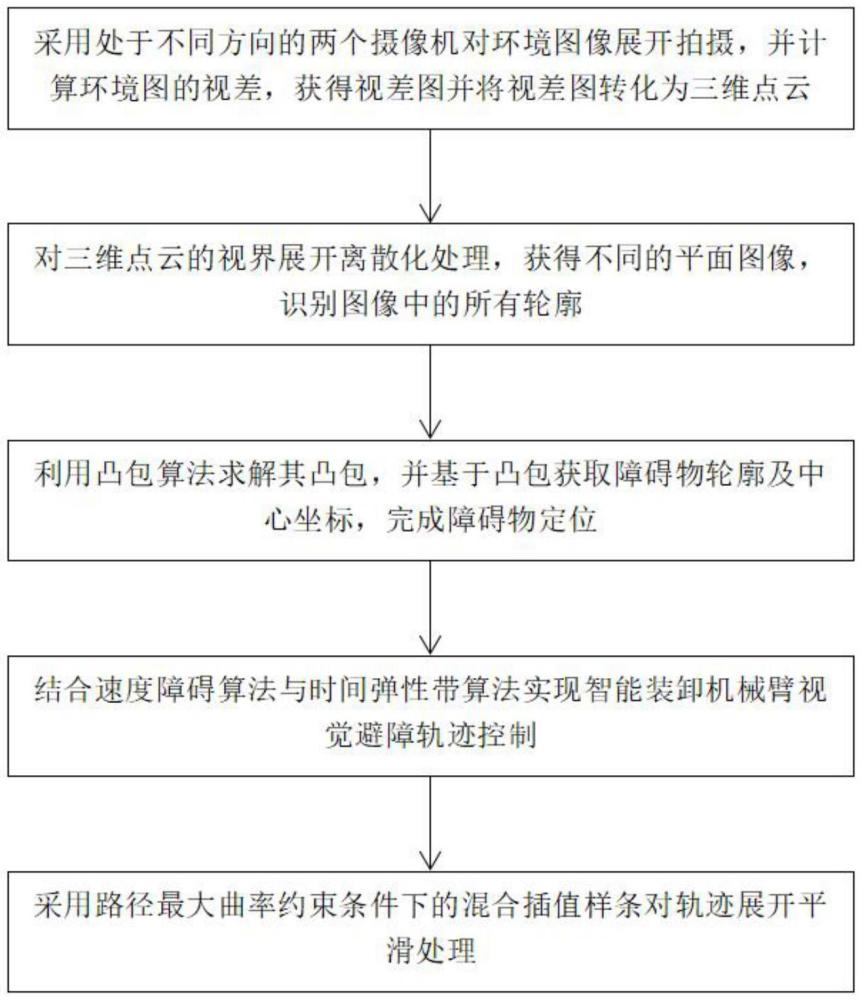
3、s1：采用处于不同方向的两个摄像机对环境图像展开拍摄，并计算环境图的视差，获得视差图并将视差图转化为三维点云；

4、s2：对三维点云的视界展开离散化处理，获得不同的平面图像，识别图像中的所有轮廓；

5、s3：对于每个得到的轮廓，可以利用凸包算法求解其凸包，并基于凸包获取障碍物轮廓及中心坐标，完成障碍物定位；

6、s4：结合速度障碍算法与时间弹性带算法实现智能装卸机械臂视觉避障轨迹控制。

7、优选的，所述步骤s1具体如下：

8、在机械臂立体视觉的基础上，采用处于不同方向的两个摄像机对环境图像展开拍摄，并计算环境图的视差，获得视差图；

9、定义重投影矩阵为w，视差为s，点坐标为(a,b)，采用相似三角形方法，获得视差图对应的三维坐标(x/e,y/e,z/e)，其中，e表示缩放因子，三维点云转化的表达式如下：

10、[x y z w]τ＝w[a b s 1]τ。

11、优选的，所述步骤s2具体如下：

12、对三维点云的视界展开离散化处理，获得不同的平面图像，并对图像展开伪彩色操作，公式如下：

13、

14、式中，q(a,b)、h(a,b)、n(a,b)表示不同像素点的rgb值；g(a,b)表示像素点在整形缩放处理后的灰度值，其值处于(0,255)区间内。因智能装卸机械臂的运动特性，设置深度阈值r，获得二值化后的图像f(a,b)；

15、

16、式中，h(a,b)表示像素点的深度值；

17、基于二值化处理后的图像f(a,b)，采用轮廓提取算法中的findcontours函数识别图像中的所有轮廓，并将每个轮廓表示为一系列的点坐标p＝[(x1,y2),(x1,y2),...,(xn,yn)]。

18、优选的，所述步骤s3具体如下：

19、对于每个得到的轮廓，利用凸包算法求解其凸包，表示为o＝[(x1,y1),(x1,y1),...,(xm,ym)]；

20、通过计算凸包的面积，得到障碍物的大小，表示如下：

21、

22、式中，pi,x、pi,y表示第i个顶点的x、y的坐标，pi+1,x、pi+1,y表示第i+1个顶点的x、y的坐标。

23、接着设置面积阈值j，筛选出凸包面积大于阈值的障碍物轮廓。对于筛选出的障碍物轮廓，计算其轮廓的重心作为障碍物的中心坐标，其表示如下：

24、

25、优选的，所述步骤s4具体如下：

26、定义不同智能装卸机械臂移动的时间间隔为δt，在该时间段内输出的控制量为c，并定义两个不同机械臂t2与t1的相对速度障碍区域集合为

27、定义t1与t2的速度分别为ct1与ct2，由此获得两者的相对速度ct2＝ct1-c12；

28、定义gst区域为t1的障碍区域，设δt间隔内ct2维持原本速度，并将t1设置成基准，对t2与其膨胀区域展开处理，获得射线dt，由此获得t1与t2的碰撞条件表示空集，满足该条件的ct2集合则是相对冲突区gp，其表达式如下：

29、

30、对gp与ct2展开闵可夫斯基矢量和运算操作，在δt内，将gp区域按照ct2速度匀速运动，获得新的绝对冲突区gq，该区域的表达式如下：

31、

32、式中，表示异或运算。根据上式可知，当c12移动末端点处于gp中时，ct1移动末端点处于gq中，此时t1与t2会产生碰撞冲突，在此基础上获得t1的速度，即计算速度为ct2时的公式如下：

33、

34、通过上述操作可知，智能机械臂的避障轨迹控制需要使机械臂规划速度ct1new满足以下条件：

35、

36、控制智能装卸机械臂的视觉避障轨迹，满足的约束。

37、优选的，还包括采用路径最大曲率约束条件下的混合插值样条对轨迹展开平滑处理，具体如下：

38、障碍物定位结果作为输入，以此为依据获得智能装卸机械臂最大转向角为αmax，其转弯半径的限制条件为t＝o/tanα，其中o表示机械臂的轴距，在此基础上计算全局路径的最大曲率lmax，公式如下：

39、lmax＝1/tmin＝(tanα)/o；

40、式中，tmin表示机械臂装卸时转弯半径的最小值；

41、将路径分割成若干份路径段，并对没有满足最大曲率约束条件的路径段展开修正，确保混合插值样条曲线每一段的最大曲率lpartmax不大于lmax，即lpartmax≤lmax；

42、当混合插值样条的一段曲率值lpartmax大于最大曲率lmax时，启动优化策略。

43、优选的，混合插值样条的一段曲率值lpartmax的计算过程如下：

44、定义混合插值样条的参数化表达式：

45、

46、式中，表示第n个路径的夹角角度；i表示样条参数向量；uj表示第j段路径的间距；在平面参数方程的基础上，对混合插值样条的曲率展开计算，公式如下:

47、

48、式中，w′(i)表示w(i)的一阶导数；v′(i)表示v(i)的一阶导数；w″(i)表示w(i)的二阶导数；v″(i)表示v(i)的二阶导数。

49、优选的，所述优化策略具体如下：

50、设智能装卸机械臂避障轨迹控制路径包含了三个控制点，分别为b1，b2与b3，其中，两端路径相交于b1点且没有满足曲率约束条件；

51、基于此对最小段长度umin展开计算：

52、

53、并将umin作为底边，获得一个新的等腰三角形，获得新的控制点b4和b5，控制点b4和b5分别为底边umin的两个端点；

54、利用底边umin的两个外角形成的两个钝角与替换处于b1点的三角形的内角并展开拟合操作，获得一条达到最大曲率要求的轨迹控制路径。

55、一种计算机可读存储介质，所述计算机可读存储介质包括存储的程序，其中，在所述程序运行时控制所述计算机可读存储介质所在设备执行如上所述的智能装卸机械臂视觉避障轨迹控制方法。

56、一种处理器，所述处理器用于运行程序，其中，所述程序运行时执行如上所述的智能装卸机械臂视觉避障轨迹控制方法。

57、与现有技术相比，本发明的有益效果为：

58、本发明首先对障碍物展开定位，为机械臂避障轨迹的规划提供了重要的输入信息。而后，本发明将速度障碍(vo)算法与时间弹性带(teb)算法相结合，提出一种全新的teb-vo算法，充分利用两者的轨迹规划能力，解决机械臂移动速度不均匀的问题与动态避碰问题，对机械臂展开速度约束，实现全局路径轨迹控制优化，避免碰撞冲突，提高机械臂的避障性能和控制精度。此外，本发明在完成轨迹控制后，进一步采用路径最大曲率约束条件下的混合插值样条对轨迹展开平滑处理，改善轨迹的连续性和平滑度，使机械臂的运动更加平滑，减少不必要的振动或突然转向，从而提高的稳定性，实现精准避障。