一种柔性关节空间机器人无速度反馈分散容错控制方法与流程

本发明属于机械臂控制，具体为一种柔性关节空间机器人无速度反馈分散容错控制方法。

背景技术：

1、近年来，随着航天技术的持续性蓬勃发展，以空间机器人为代表的先进航天器受到日益广泛的关注。空间机器人可在极限温差、超强辐射、几近失重的太空环境中辅助或替代航天员执行复杂、高危的出舱任务，在提升工作效率和保障航天员生命安全方面发挥着无与伦比的作用。考虑到操作窗口时间的限制，空间机器人需要在固定时间内快速捕获并拖拽目标物体，但由于机械臂关节内部的齿轮谐波减速器的传动作用，机械臂连杆的转动与关节电机的转动不能同步，即两者存在转角偏差，从而造成关节铰的柔性振动。目前，从已有的资料来看，对于柔性臂空间机器人动力学及减振控制的研究较为成熟，通常采用奇异摄动法，而奇异摄动法无法应用于关节刚度较小的机器人系统。

2、需要指出的是，由于太空带电粒子射流与太阳磁场的影响，空间机器人自身传感仪器及执行器件极易发生未知失效故障，导致出现模型不确定和速度信号无法获取问题，从而无法稳定跟踪期望轨迹。然而，同时考虑上述两类故障的空间机器人的容错控制相关研究暂未见报道。有鉴于此，本发明借助速度观测器与分散神经网络为柔性关节空间机器人设计了一种无速度反馈分散容错控制方法。

技术实现思路

1、本发明旨在至少解决现有技术中存在的技术问题之一；为此，本发明提出了一种柔性关节空间机器人无速度反馈分散容错控制方法，用于解决传感器与执行器故障、模型不确定和速度信号无法获取的技术问题。

2、为实现上述目的，本发明提供一种柔性关节空间机器人无速度反馈分散容错控制方法，包括以下步骤：

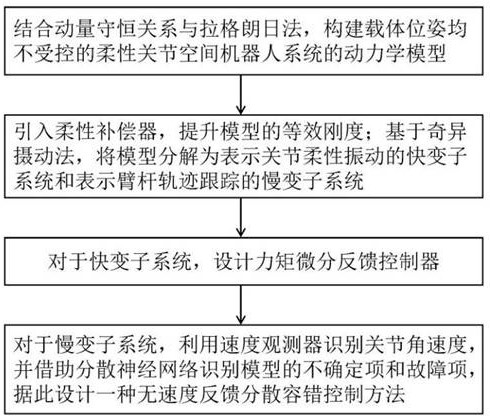
3、s1：结合动量守恒关系与拉格朗日法，构建载体位姿均不受控的柔性关节空间机器人系统的动力学模型；

4、s2：引入柔性补偿器，提升模型的等效刚度；基于奇异摄动法，将模型分解为表示关节柔性振动的快变子系统和表示臂杆轨迹跟踪的慢变子系统；

5、s3：对于快变子系统，设计力矩微分反馈控制器；

6、s4：对于慢变子系统，利用速度观测器识别关节角速度，并借助分散神经网络识别模型的不确定项和故障项，据此设计一种无速度反馈分散容错控制方法。

7、进一步地：所述s1的具体实现过程为：

8、结合系统角动量、线动量守恒关系与拉格朗日法，可得载体位姿均不受控的柔性关节空间机器人系统的完全驱动形式的动力学方程如下所示：

9、      （1）

10、                       （2）

11、                      （3）

12、其中，为系统对称、正定惯量矩阵；为系统包含科氏力、离心力的列向量；为柔性关节铰所传递的控制力矩列向量；为关节驱动电机的控制力矩列向量；；为机械臂转角列向量；为驱动电机转子转角列向量；为驱动电机正定惯量矩阵；为关节刚度系数矩阵。

13、进一步地：所述s2的具体实现过程为：

14、对所述s1确定的柔性关节空间机器人系统的动力学模型，采用奇异摄动法进行控制器的设计；

15、首先，由s1确定的柔性关节空间机器人系统的动力学模型可得；

16、                  （4）

17、其中，为驱动电机正定惯量矩阵；

18、为关节刚度系数矩阵；

19、为关节驱动电机的控制力矩列向量；

20、为柔性关节铰所传递的控制力矩列向量，表示相对于时间t的二阶导数；

21、为空间机器人机械臂转角列向量，表示相对于时间t的二阶导数；

22、驱动电机的控制律设计为：

23、                    （5）

24、其中，为新引进的关节柔性补偿控制器，为对角、正定柔性补偿矩阵；，为单位矩阵；为待设计的控制输入量；

25、将上述公式（5）和（4）整理可得：

26、                （6）

27、其中，为经过柔性补偿后的等效刚度矩阵，通过调整即可改变；

28、所述s1确定的柔性关节空间机器人系统的动力学模型与公式(6)组成了经过柔性补偿后的柔性关节空间机器人的动力学模型；

29、结合奇异摄动法，可将分解成两部分，如下所示：

30、                       (7)

31、其中，和分别表示柔性关节空间机器人的快变与慢变子系统控制律；

32、假定刚度系数矩阵中最小刚度为，定义奇异摄动因子为：，令，则为与慢变分量拥有同一数量级别的对角、正定常数矩阵；

33、结合式(6)与式(7)，可导出快变子系统的动力学方程为:

34、            (8)

35、此时，若令，则且。

36、进一步地：所述s4中的慢变子系统具体为：将所述s3中的快变子系统代入所述s1确定的柔性关节空间机器人系统的动力学模型可得柔性关节空间机器人的慢变子系统动力学方程为：

37、                       (9)

38、其中，为正定惯性矩阵；为利用化简整理后得到的列向量；

39、表示相对于时间t的二阶导数。

40、进一步地：所述s3的具体实现过程为：

41、对所述s2中的快变子系统，为了抑制由柔性关节引起的弹性振动，设计力矩微分反馈控制器为：

42、                       (10)

43、其中，为对角系数矩阵；

44、为定义的奇异摄动因子；

45、为柔性关节铰所传递的控制力矩列向量，表示相对于时间t的一阶导数。

46、进一步地：所述s4的具体实现过程为：

47、为了实现对关节运动的单独控制，将每个关节模块考虑为一个二阶子系统，从所述慢变子系统中分离出局部变量，则慢变子系统的分散动力学模型可以表示为：

48、   (11)

49、(12)

50、其中，为二阶子系统的惯性参数项；为二阶子系统的科氏力、离心力项；、、与分别为向量、、与的第i个元素；与分别为矩阵与的第ij个元素；为二阶子系统交联项；

51、对于关节执行器发生效率损失故障的空间机器人，其慢变子系统的分散动力学方程可描述为：

52、            (13)

53、其中，表示故障因子，满足，其值越小表示对应执行器的故障情况越严重；

54、定义二阶子系统的状态向量，则式(13)可写成如下的状态空间方程：

55、    (14)

56、其中，；

57、；

58、；

59、二阶子系统的速度观测器设计为：

60、             (15)

61、其中，和分别为和的估计值，为饱和函数；

62、当系统关节的期望轨迹、与存在且有界；

63、定义二阶子系统的位置误差向量为：

64、                        (16)

65、二阶子系统的位置环积分滑模函数设计为：

66、                     (17)

67、其中，为正常数；

68、将式(17)对时间t求导，可得：

69、            (18)

70、当，存在很小的正数，满足：

71、                         (19)

72、将式(19)代入式(18)，可得

73、          (20)

74、定义二阶子系统的虚拟角速度为

75、(21)

76、其中，为正常数，为符号函数；

77、定义虚拟角速度跟踪误差为：

78、                          (22)

79、二阶子系统的速度环积分滑模函数设计为：

80、                      (23)

81、其中，为正常数；

82、将式(23)对时间t求导，可得：

83、     (24)

84、借助rbf(radial basis function)神经网络对二阶子系统的不确定项与未知项进行重构，假定理想神经网络函数表达式如下：

85、 (25)

86、 (26)

87、其中，与为理想神经网络权值；

88、与为神经网络基函数；

89、与为神经网络逼近误差，为未知正常数；

90、定义与分别为与的估计值，与为神经网络高斯基函数；则与的实际rbf神经网络输出分别为：

91、                    (27)

92、                       (28)

93、定义神经网络权值估计误差为，，基函数估计误差为，，结合式（25）至（28），有：

94、     (29)

95、            (30)

96、当二阶子系统的交联项有界且满足：

97、              (31)

98、其中，，；

99、利用式（32）的神经网络补偿交联项对二阶子系统的影响：

100、               (32)

101、其中，为神经网络表达式，为理想神经网络权值的估计值，为神经网络基函数的估计值；

102、定义二阶子系统的神经网络最小逼近误差如下:

103、         (33)

104、                 (34)

105、         (35)

106、其中，。

107、神经网络权值,与依次按下面的自适应律更新：

108、                         (36)

109、                        (37)

110、                         (38)

111、二阶子系统的速度环积分滑模容错控制律设计为：

112、    (39)

113、其中，与均为正常数。

114、本发明的有益技术效果为：

115、1.在引入奇异摄动法的基础上还设计了一种柔性补偿器，提高了关节的等效刚度，解决了奇异摄动法无法应用于关节刚度较小的机器人系统的问题。

116、2.本发明为柔性关节空间机器人慢变子系统设计了一种无速度反馈分散容错控制方法，解决了传感器、执行器并发故障下空间机器人的运动控制问题。利用速度观测器识别关节角速度，借助分散神经网络重构模型不确定项和故障项，全面提升空间机器人的任务执行效率。

117、3.本发明为柔性关节空间机器人的快变子系统设计了一种力矩微分反馈控制器，抑制由柔性关节引起的弹性振动，确保机械臂可以稳定跟踪期望轨迹。