一种遥操作中利用隐马尔可夫模型和双层贝叶斯计算期望速度的方法及系统

本发明属于机器人遥操作相关，更具体地，涉及一种遥操作中利用隐马尔可夫模型和双层贝叶斯计算期望速度的方法及系统。

背景技术：

1、遥操作技术中依赖操作员的运动来控制从端机器人运动，通常从端机器人只是严格的复制主端操作员人手的轨迹。但是由于生理上的原因，人手在运动过程中的抖动是不可避免的，如果直接将包含抖动干扰的指令发送给从端机器人，将严重影响速度的稳定性和轨迹的平滑性。因此需要进行人手抖动的抑制。

2、卡尔曼滤波器可以预测人手的抖动信号并进行过滤，但其对非线性信号的预测精度不高。机器学习方法比如支持向量机和神经网络同样可以应用于消除人手抖动，且适用于非线性系统，但是其仅从数据层面上过滤人手的高频小幅度抖动信号，不能从完成任务的意图的层面抑制由累积抖动造成的低频大幅度信号。操作员在已经意识到任务所需的路径的情况下仍会产生造成抖动信号的根本原因是人类行为的随机性，因此需要对该随机性进行表征。

3、隐马尔可夫模型已经被用于可以表征人类行为的随机性，利用隐马尔可夫模型对人的意图也就是人手移动的期望速度进行识别可以达到过滤抖动信号的功能。目前，现有的利用进行抖动的消除仅仅限于对于直线轨迹的抖动消除，在更多应用场景比如遥操作涂胶中任务轨迹是多样的，仅仅利用隐马尔可夫模型缺乏对多样化轨迹的适应性。因此，亟需一种方法可以适用于遥操作的抖动消除中。

技术实现思路

1、针对现有技术的以上缺陷或改进需求，本发明提供了一种遥操作中利用隐马尔可夫模型和双层贝叶斯计算期望速度的方法及系统，解决复杂轨迹遥操作任务中的人手抖动抑制的问题。

2、为实现上述目的，按照本发明的一个方面，提供了一种遥操作中利用隐马尔可夫模型和双层贝叶斯计算期望速度的方法，该方法包括下列步骤：

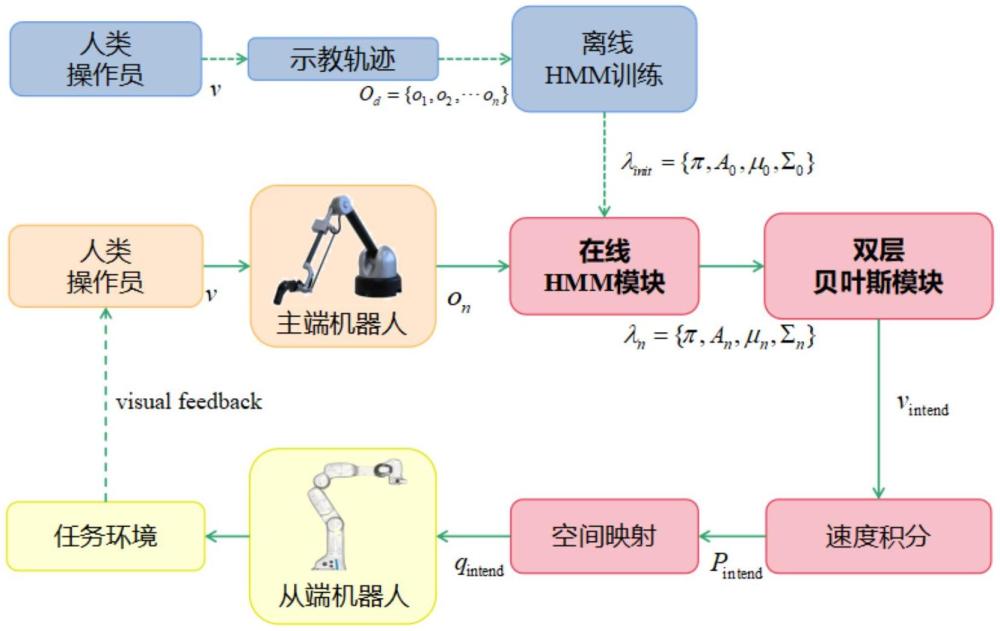
3、获取主端机器人离线运动中的离线运动轨迹，利用该离线运动轨迹离线训练隐马尔可夫模型直至收敛，以此确定所述隐马尔可夫模型中的模型参数，所述隐马尔可夫模型中主端机器人的速度为可观测状态，从端机器人的期望速度为隐状态；

4、在训练后的隐马尔可夫模型中输入主端机器人当前时刻的运动速度，获得该当前时刻的运动速度对应的隐马尔可夫模型参数；利用贝叶斯公式计算所述隐马尔可夫模型中每个隐状态在当前时刻出现的概率；再次利用贝叶斯公式并结合当前时刻每个隐状态出现的概率计算下一时刻每个隐状态出现的概率，利用下一时刻每个隐状态出现的概率计算当前时刻从端机器人的期望速度。

5、进一步优选地，离线训练所述隐马尔可夫模型后，对该离线训练所述隐马尔可夫模型进行在线训练，在线训练的过程如下：

6、在线获取主端机器人各个时刻的实时运动速度，然后将该实时运动速度输入离线训练后的所述隐马尔可夫模型中进行训练，以此在线训练过程。

7、进一步优选地，所述利用贝叶斯公式计算所述隐马尔可夫模型中每个隐状态在当前时刻出现的概率的公式如下：

8、

9、其中，是n时刻隐状态为zi的概率，是n时刻观测状态为{o1,o2,…,on}且隐状态为zi的概率，i∈{1,2,…m}是隐状态的编号，m是隐状态的总数量。

10、进一步优选地，所述前向因子的计算公式如下：

11、

12、其中，是1时刻观测状态为o1且隐状态为zi的概率；πi是1时刻隐状态为zi的概率；p(o1|s1＝zi)是在1时刻隐状态为zi的条件下，可观测状态为o1的概率；是n+1时刻观测状态为{o1,o2,…,on,on+1}且隐状态为zi的概率；aij＝p(sn+1＝zj|sn＝zi)是n时刻隐状态为zi的条件下，n+1时刻隐状态为zj的概率；p(on+1|sn+1＝zi)是在n+1时刻隐状态为zi的条件下，可观测状态为on+1的概率；是在n时刻观测状态为{o1,o2,…,on}且隐状态为zi的概率；i∈{1,2,…m}是当前时刻隐状态的编号，j∈{1,2,…m}是下一时刻隐状态的编号，m是隐状态的总数量。

13、进一步优选地，所述再次利用贝叶斯公式并结合隐马尔可夫模型参数中当前时刻的状态转移矩阵计算下一时刻各个隐状态出现的概率，按照下列公式进行：

14、

15、其中，是在n+1时刻隐状态为zi的概率；aij＝p(sn+1＝zj|sn＝zi)是当前时刻隐状态为zi的条件下，下一个隐状态为zj的概率；是在n时刻隐状态为zi的概率，i∈{1,2,…m}是当前时刻隐状态的编号，j∈{1,2,…m}是下一时刻隐状态的编号，m是隐状态的总数量。

16、进一步优选地，所述利用下一时刻各个隐状态出现的概率计算当前时刻从端机器人的期望速度，按照下列公式进行：

17、

18、其中，vn,intend是当前n时刻从端机器人的期望速度；是在n+1时刻隐状态为zi的概率，是在n时刻隐状态为zi的条件下可观测状态为on所满足的高斯概率分布的均值，i∈{1,2,…m}是当前时刻隐状态的编号。

19、进一步优选地，所述按照下列公式计算：

20、

21、其中，μi是在当前时刻隐状态为zi的条件下可观测状态为on所满足的高斯概率分布p(on|sn＝zi)的均值，是该高斯概率分布的一阶充分统计量，表示在当前时刻可观测状态为{o1,o2,...,on}的条件下隐状态zi在所有时刻出现的次数的均值，是该高斯概率分布二阶充分统计量，表示在当前时刻可观测状态为{o1,o2,...,on}的条件下出现隐状态zi时对应的可观测状态的累加和的均值，i∈{1,2,…m}是当前时刻隐状态的编号。

22、进一步优选地，在获得当前时刻从端机器人的期望速度后，利用该期望速度计算获得当前时刻从端机器人的关节空间位置，以此对所述从端机器人进行控制。

23、进一步优选地，利用该期望速度计算获得当前时刻从端机器人的关节空间位置按照如下步骤进行：

24、对当前时刻机器人的期望速度进行积分获得当前时刻从端机器人的期望位置pintend；

25、利用增量式空间映射方法将所述从端机器人的期望位置映射到从端机器人的基坐标系下获得从所述端机器人期望位置的笛卡尔空间位置ps；

26、利用机器人的逆运动学将所述笛卡尔空间位置ps转化为机器人关节空间位置qintend。

27、按照本发明的另一个方面，提供了一种遥操作中利用隐马尔可夫模型和双层贝叶斯计算期望速度的系统，该系统包括执行器，该执行器用于执行上述所述的一种遥操作中利用隐马尔可夫模型和双层贝叶斯计算期望速度的方法。

28、总体而言，通过本发明所构思的以上技术方案与现有技术相比，具备下列有益效果：

29、1.本发明中利用隐马尔可夫模型作为基础模型结合双层贝叶斯算法，识别遥操作中操作员平滑移动主端机器人的意图，计算隐藏在人手抖动轨迹下的，操作员主观意图上希望实现的期望轨迹；该轨迹即为消除人手抖动后的平滑轨迹，从而实现遥操作任务中的人手抖动抑制。

30、2.本发明在利用实际运动速度获得隐马尔可夫模型参数后，第一次采用贝叶斯算法计算各个隐状态出现的概率，然后再次利用贝叶斯算法计算下一个时刻隐状态出现的概率。由于人类存在反应时间，所以会在后一个时间步对当前时刻的抖动做出调整，即当前时刻的真实期望速度会在下一个时刻体现出来，因此最后利用下一时刻隐状态出现的概率计算当前时刻的期望速度，实现更加准确的期望速度计算。

31、3.本发明对于隐马尔可夫模型进行离线训练之后，再利用离线训练的模型作为在线训练的初始模型，实现隐马尔可夫模型的离线训练和在线训练两个训练过程，使得在执行遥操作任务的同时进行隐马尔可夫模型参数的更新，从而识别到不同于离线训练轨迹中新的操作员意图，实现对不局限于离线轨迹的任意复杂轨迹的人手抖动抑制。