一种高浓磨浆系统经济优化运行控制方法及系统与流程

本发明涉及制浆和造纸过程控制技术领域，具体是一种高浓磨浆系统经济优化运行控制方法及系统。

背景技术：

高浓磨浆系统作为化学热磨机械制浆生产过程中的主要工序，是典型的高能耗、低效率过程，据统计，高浓磨浆系统的电能消耗一般占到制浆生产过程用电的60％以上。所以，其生产运行状况不仅直接决定着整个制浆过程的生产能耗，而且也直接影响到纸浆质量的均匀性和稳定性。为了获得良好的经济效益和高质量纸浆，目前高浓磨浆系统面临着降低电能消耗、减小环境污染(如温室气体排放)和为后续抄纸工序提供更加稳定纸浆等一系列挑战。

高浓磨浆系统是典型的具有多变量、强耦合、时滞、时变等特征复杂工业过程，使得高浓磨浆系统的机理分析、建模和控制存在很大困难。目前国内外广泛采用比边缘负荷理论和比表面负荷获得的高浓磨浆系统的机理模型，但其在分析和建模过程中假设性强，不足以有效表征整个高浓磨浆过程，截止目前，很难找到一个足以表征整个高浓磨浆过程的机理模型，这使得目前存在高浓磨制浆的机理模型无法满足当今制浆和造纸生产过程控制的需要。

游离度CSF作为目前国际上衡量纸浆质量的主要指标之一，其可实现在线检测，与高浓磨浆系统的能耗息息相关。为此，通常采用CSF来直接评价高浓磨浆过程的产品质量。因此，为最终实现高浓磨浆系统生产的连续化和规模化，寻求一种不但生产能耗低，而且可获得质量均匀、稳定纸浆的先进控制技术，也是当前制浆和造纸工业领域亟待解决的关键问题之一。

高浓磨浆系统运行和控制问题直接关系到后续造纸环节的能耗及纸质产品质量，更影响整个造纸和制浆企业的经济成本。然而，高浓磨浆系统最终的控制目标不仅仅是希望获得企业期望的纸浆质量，而且要确保在生产过程最小的能量消耗，使企业在生产过程获得最大的经济效益。但目前高浓磨浆系统的控制均是对系统的运行状态变量的控制，纸浆质量工艺指标值通常是实验室化验获得，但是化验周期严重滞后，严重影响高浓磨浆系统经济优化运行和产品质量的有效控制，高浓磨浆系统自身的复杂动态特性以及在线测量仪器的局限，使得高浓磨浆系统的运行状态实时监测与控制变得极其困难。近年来，新型在线检测纸浆质量指标游离度仪器的出现，可快速、准确检测纸浆游离度，已确定是否满足企业要求，这些都为高浓磨浆系统的纸浆质量在线控制提供了可能。因此，实现高浓磨浆系统的经济优化运行和纸浆质量的在线控制对制浆和造纸工业将会产生重要的作用。

技术实现要素：

针对现有技术存在的问题，本发明提供一种高浓磨浆系统经济优化运行控制方法及系统。

本发明的技术方案是：

一种高浓磨浆系统经济优化运行控制方法，包括：

步骤1、采集高浓磨浆系统的螺旋喂料量、磨盘压力、稀释水流量、产量、磨机负荷、纸浆浓度；

步骤2、利用高浓磨浆系统纸浆质量指标游离度输出模型得到经济性能指标函数最小时的操作变量；

所述高浓磨浆系统纸浆质量指标游离度输出模型的操作变量为螺旋喂料量、磨盘压力、稀释水流量，状态变量为磨机处理量、磨机负荷、纸浆浓度，输出变量为纸浆质量指标游离度；

步骤3、将经济性能指标函数最小时的操作变量作为操作变量的最优值，下发到高浓磨浆系统的执行机构，实现高浓磨浆系统经济优化运行和纸浆质量指标游离度的控制。

所述步骤2包括：

步骤2-1、采用带控制量自回归模型构建螺旋喂料量与磨机处理量的线性关系模型、磨盘压力与磨机负荷的线性关系模型、稀释水流量与纸浆浓度的线性关系模型，作为一个线性动态子系统；

三个线性关系模型的输入变量分别为螺旋喂料量、磨盘压力、稀释水流量；三个线性关系模型的输出变量分别为磨机处理量、磨机负荷、纸浆浓度；

步骤2-2、采用Hankel矩阵秩估计定阶方法分别估计三个线性关系模型阶次；

步骤2-3、采用偏差补偿最小二乘递推算法辨识出三个线性关系模型所对应的带控制量自回归模型中的参数；

步骤2-4、将三个线性关系模型的输出变量作为高浓磨浆系统纸浆质量指标游离度输出模型的状态变量，将纸浆质量指标游离度作为输出变量，建立输出变量与状态变量之间的机理模型，作为非线性静态子系统；

步骤2-5、利用线性关系模型和输出变量与状态变量之间的机理模型，建立高浓磨浆系统纸浆质量指标游离度输出模型，高浓磨浆系统纸浆质量指标游离度输出模型即由一个线性动态子系统和一个非线性静态子系统串联的Wiener模型；

步骤2-6、利用序列二次规划算法优化高浓磨浆系统运行的经济性能指标函数，获得最优操作变量。

所述步骤2-6，包括：

步骤2-6-1、设定操作变量约束条件、状态变量约束条件、输出的纸浆质量指标游离度约束条件；

步骤2-6-2、利用序列二次规划算法优化高浓磨浆系统运行的经济性能指标函数，所述经济性能指标函数为能耗目标的加权和控制目标的加权，经济性能指标函数最小时的操作变量为最优的操作变量。

所述的高浓磨浆系统经济优化运行控制方法采用的高浓磨浆系统经济优化运行控制系统，包括：

采集单元：采集高浓磨浆系统的螺旋喂料量、磨盘压力、稀释水流量、产量、磨机负荷、纸浆浓度；

操作变量优化单元：利用高浓磨浆系统纸浆质量指标游离度输出模型得到经济性能指标函数最小时的操作变量；高浓磨浆系统纸浆质量指标游离度输出模型的操作变量为螺旋喂料量、磨盘压力、稀释水流量，状态变量为磨机处理量、磨机负荷、纸浆浓度，输出变量为纸浆质量指标游离度；

运行控制单元：将经济性能指标函数最小时的操作变量作为操作变量的最优值，下发到高浓磨浆系统的执行机构，实现高浓磨浆系统经济优化运行和纸浆质量指标游离度的有效控制。

所述操作变量优化单元，包括：

第一子系统建立模块：采用带控制量自回归模型构建螺旋喂料量与磨机处理量的线性关系模型、磨盘压力与磨机负荷的线性关系模型、稀释水流量与纸浆浓度的线性关系模型，作为一个线性动态子系统；三个线性关系模型的输入变量分别为螺旋喂料量、磨盘压力、稀释水流量；三个线性关系模型的输出变量分别为磨机处理量、磨机负荷、纸浆浓度；

阶次估计模块：采用Hankel矩阵秩估计定阶方法分别估计三个线性关系模型阶次；

参数辨识模块：采用偏差补偿最小二乘递推算法辨识出三个线性关系模型所对应的带控制量自回归模型中的参数；

第二子系统建立模块：将三个线性关系模型的输出变量作为高浓磨浆系统纸浆质量指标游离度输出模型的状态变量，将纸浆质量指标游离度CSF作为输出变量，建立输出变量与状态变量之间的机理模型，作为非线性静态子系统；

模型建立模块：利用线性关系模型和输出变量与状态变量之间的机理模型，建立高浓磨浆系统纸浆质量指标游离度输出模型，高浓磨浆系统纸浆质量指标游离度输出模型即由一个线性动态子系统和一个非线性静态子系统串联的Wiener模型；

操作变量优化模块：利用序列二次规划算法优化高浓磨浆系统运行的经济性能指标函数，获得最优操作变量。

所述操作变量优化模块，包括：

约束条件设定模块：设定操作变量约束条件、状态变量约束条件、输出的纸浆质量指标游离度约束条件；

优化模块：利用序列二次规划算法优化高浓磨浆系统运行的经济性能指标函数，所述经济性能指标函数为能耗目标的加权和控制目标的加权，经济性能指标函数最小时的操作变量为最优的操作变量。

有益效果：

本发明基于化学机械制浆生产线上传感器测量的高浓盘磨机输入输出相关数据，结合Hankel矩阵秩定阶方法确定线性动态子系统中线性关系模型结构和偏差补偿最小二乘递推辨识算法获得子线性关系模型参数，并结合以纸浆质量指标游离度输出变量与线性关系模型输出变量之间的机理模型，建立表征整个高浓磨浆系统以纸浆质量指标游离度为输出变量的Wiener结构模型，基于模型预测控制理论，利用序列二次规划算法优化系统的经济性能指标函数，获得最优操作变量，实现对高浓磨浆系统的经济优化运行和纸浆质量指标游离度CSF有效控制，从而指导实际生产操作，具有重要的实际工程意义。

附图说明

图1是高浓磨浆系统工艺流程图，其中：1-预蒸仓，2-喂料螺旋传送器，3-预处理后木片，4-稀释水，5-磨机定盘，6-磨机动盘，7-液压缸，8-液压缸，9-蒸汽，10-纸浆；

图1所用标记符号如下：

螺旋喂料量——u₁(kg/min)

磨盘压力——u₂(N)

稀释水流量——u₃(kg/min)

磨机处理量——x₁(t/day)

磨机负荷——x₂(Mw)

纸浆浓度——x₃(％)；

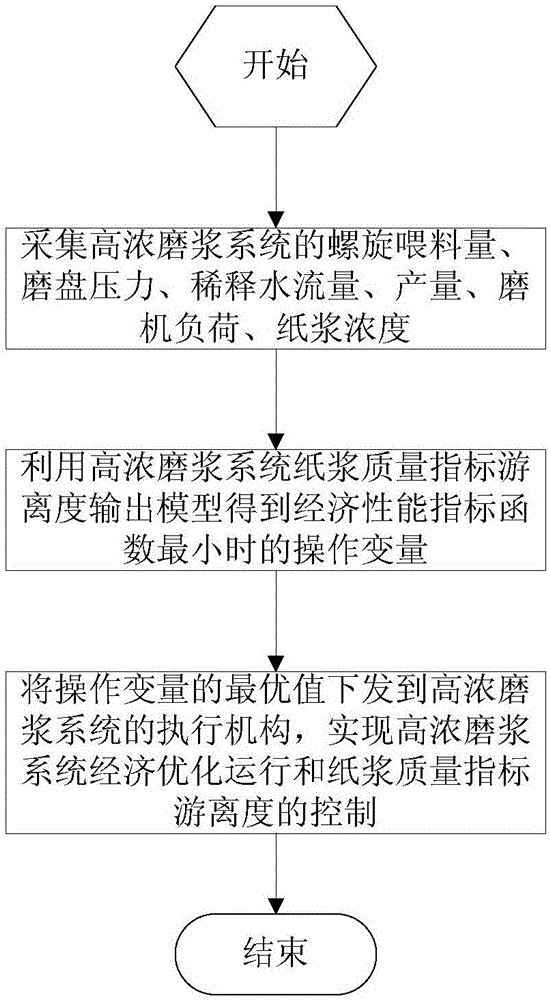
图2是本发明具体实施方式中高浓磨浆系统经济优化运行控制方法流程图；

图3是本发明具体实施方式中子系统在不同模型阶次下对应的Hankel矩阵行列式比；

图4是本发明具体实施方式中线性关系模型参数估计值变化图；

图5是本发明具体实施方式中建立的线性关系模型输出和真实输出变化图；

图6是本发明具体实施方式中建立的线性关系模型输出和真实输出之间误差变化图；

图7是本发明具体实施方式中的Wiener模型结构图；

图7所用标记符号如下：

纸浆质量指标游离度CSF(ml)和子系统输出变量之间非线性函数——f(·)；

图8是本发明具体实施方式中螺旋喂料量u₁输入变化图；

图9是本发明具体实施方式中磨盘压力u₂输入变化图；

图10是本发明具体实施方式中稀释水流量u₃输入变化图；

图11是本发明具体实施方式中高浓磨机处理量x₁输出变化图；

图12是本发明具体实施方式中磨机负荷x₂输出变化图；

图13是本发明具体实施方式中纸浆浓度x₃输出变化图；

图14是本发明具体实施方式中高浓磨浆系统比能耗变化图；

图15是本发明具体实施方式中纸浆质量指标游离度CSF(ml)设定值跟踪变化图；

图16是本发明具体实施方式中经济性能指标函数变化图；

图17是本发明具体实施方式中高浓磨浆系统经济优化运行控制方法步骤2流程图；

图18是本发明具体实施方式中高浓磨浆系统经济优化运行控制方法步骤2-6流程图；

图19是本发明具体实施方式中高浓磨浆系统经济优化运行控制系统框图；

图20是本发明具体实施方式中高浓磨浆系统经济优化运行控制系统的操作变量优化单元框图；

图21是本发明具体实施方式中高浓磨浆系统经济优化运行控制系统的操作变量优化模块框图。

具体实施方式

下面结合附图对本发明的具体实施方式做详细说明。

高浓磨浆系统工艺流程如图1所示，将送入预蒸仓1中木片进行预处理后，预处理木片3在喂料螺旋传送器2作用下送入磨区，同时注入磨区一定量的稀释水4，在液压缸7驱动下，使预处理后木片3在磨机定盘5和动盘6之间进行研磨后的浆料在汽浆分离器8作用下，排出蒸汽9，最终获得满足生产需求的纸浆10。

高浓磨浆系统的输入变量为螺旋喂料量u₁(kg/min)、磨盘压力u₂(N)、稀释水流量u₃(kg/min)，状态变量为磨机处理量x₁(t/day)、磨机负荷x₂(Mw)、纸浆浓度x₃(％)，输出变量为纸浆质量指标游离度CSF(ml)。本实施方式通过对化学机械制浆生产线上在线实时采集数据，获取100组输入输出数据进行高浓磨浆系统的经济优化运行和纸浆质量指标游离度CSF控制。

本实施方式的高浓磨浆系统经济优化运行控制方法，如图2所示，包括：

步骤1、采集高浓磨浆系统的螺旋喂料量u₁、磨盘压力u₂、稀释水流量u₃、产量x₁、磨机负荷x₂、纸浆浓度x₃；

螺旋喂料量u₁、磨盘压力u₂、稀释水流量u₃、磨机处理量x₁、磨机负荷x₂、纸浆浓度x₃的数据可以在高浓磨浆系统中直接提取。

步骤2、利用高浓磨浆系统纸浆质量指标游离度输出模型得到经济性能指标函数最小时的操作变量；

所述高浓磨浆系统纸浆质量指标游离度输出模型的操作变量为螺旋喂料量u₁、磨盘压力u₂、稀释水流量u₃，状态变量为磨机处理量x₁、磨机负荷x₂、纸浆浓度x₃，输出变量为纸浆质量指标游离度CSF(ml)；

如图17所示，所述步骤2包括：

步骤2-1、采用带控制量自回归模型构建螺旋喂料量u₁与磨机处理量x₁的线性关系模型、磨盘压力u₂与磨机负荷x₂的线性关系模型、稀释水流量u₃与纸浆浓度x₃的线性关系模型，作为一个线性动态子系统；

三个线性关系模型的输入变量分别为螺旋喂料量u₁、磨盘压力u₂、稀释水流量u₃；三个线性关系模型的输出变量分别为磨机处理量x₁、磨机负荷x₂、纸浆浓度x₃；

以螺旋喂料量u₁与磨机处理量x₁的线性关系模型为例说明如下：

式中，A₁₍z^-1)、B₁(z^-1)表示z^-1的多项式，e(k)为白噪声干扰，d₁为纯延迟，k为采样时刻，且有k＝1，2，…，L，L为数据长度。

式中，n_a、n_b分别为多项式A₁(z^-1)、B₁(z^-1)的阶次，也即螺旋喂料量u₁与磨机处理量x₁的线性关系模型的阶次；

螺旋喂料量u₁与磨机处理量x₁的线性关系模型可以写成最小二乘形式：

其中，h(k)和θ分别为输入/输出数据和待估参数。

状态变量和操作变量的线性关系构成线性方程即螺旋喂料量u₁与磨机处理量x₁的线性关系模型：

x_L(k)＝h_L(k)θ+e_L(k)

其中，x_L(k)＝[x₁(1)，x₁(2)，…，x₁(k)]^T，e_L(k)＝[e(1)，e(2)，…，e(k)]^T

步骤2-2、采用Hankel矩阵秩估计定阶方法分别估计三个线性关系模型阶次。

假设脉冲响应序列为g(1)，g(2)，…，g(L)，L为脉冲序列长度即数据长度，Hankel矩阵定义如下：

其中，l决定Hankel矩阵的维数，k可以在1和(L-2l+2)之间选择。

根据Hankel矩阵的性质

式中，n为线性关系模型的真实阶次，如果Hankel矩阵元素由于噪声和误差存在，Hankel矩阵H(l，k+1)的行列式在大多数情况下不能保证为零，但是其行列式值通常会急剧下降，维持采用行列式平均比值作为判别Hankel矩阵是否为奇异阵准则，即

当l从1逐渐增加到(n+1)时，式中D(l)会有较大幅度的下降，此时在l＝n处获得最大值，这时可取出现最大值时的l作为线性关系模型的最佳阶次估计值。

步骤2-3、采用偏差补偿最小二乘递推算法辨识出三个线性关系模型所对应的带控制量自回归模型中的参数；

当三个线性关系模型阶次确定后，利用偏差补偿最小二乘递推算法辨识获得三个线性关系模型参数估计值，具体算法如下：

式中，和分别为最小二乘参数估计值和补偿最小二乘参数估计值；J(k)和为最小二乘意义下的损失函数和新息；和D分别为噪声ξ(k)的方差估计和常数阵。

设置初始值和P(0)＝I，输入初始数据，采样当前k时刻输出x₁(k)和输入u₁(k)，计算

利用Henkel矩阵秩估计模型阶次和偏差补偿最小二乘递推辨识算法容易确定螺旋喂料量u₁(kg/min)和磨机处理量x₁(t/day)、磨盘压力(N)和磨机负荷x₂(Mw)、稀释水流量u₃(kg/min)和纸浆浓度x₃(％)线性关系模型结构。以建立螺旋喂料量u₁(kg/min)和磨机处理量x₁(t/day)之间线性关系模型为例，假设n_a＝n_b，其行列式比随阶次变化趋势及模型参数估计值分别如图3和图4所示。所建立的线性关系模型输出与实际输出如图5所示，线性关系模型输出与实际输出之间误差如图6所示。同理，并最终得到三个线性关系模型的参数估计值分别为

表1.线性关系模型阶次和模型参数估计值

步骤2-4、将三个线性关系模型的输出变量作为高浓磨浆系统纸浆质量指标游离度输出模型的状态变量，将纸浆质量指标游离度CSF作为输出变量，建立输出变量与状态变量之间的机理模型，作为非线性静态子系统；

定义高浓磨浆系统比能耗(SE)和磨浆强度(I)如下：

其中，M为磨机负荷x₂，P为高浓磨浆系统的磨机处理量x₁，磨浆次数N为

其中，n表示单位弧长的磨齿数，ω为磨机转速，r₂和r₁分别为磨区内半径、磨区外半径，t为浆料停留时间。

基于高浓磨浆系统比能耗(SE)和磨浆强度(I)，纸浆质量指标游离度CSF与状态变量之间的机理模型为：

其中，CSF₀、SE₀和I₀分别为游离度CSF的初始值、磨机比能耗的初始值和磨浆强度的初始值，k₁，k₂为常数。

步骤2-5、利用线性关系模型和输出变量与状态变量之间的机理模型，建立高浓磨浆系统纸浆质量指标游离度输出模型，高浓磨浆系统纸浆质量指标游离度输出模型即由一个线性动态子系统和一个非线性静态子系统串联的Wiener模型；

分别以螺旋喂料量u₁(kg/min)、磨盘压力u₂(N)、稀释水流量u₃(kg/min)为输入变量(操作变量)，分别以磨机处理量x₁(t/day)、磨机负荷x₂(Mw)、纸浆浓度x₃(％)为状态变量，输出变量为纸浆质量指标游离度CSF(ml)，建立高浓磨浆系统纸浆质量指标游离度输出模型，此模型是由一个线性动态子系统和一个非线性静态子系统串联的Wiener模型，如图7所示，其描述如下：

其中，A和B为后移算子z-1的多项式，e(k)为白噪声，△＝1-z-1，h(·)为非线性状态函数，f(·)为纸浆质量指标游离度CSF(m1)和状态变量之间的非线性函数，d为纯滞后时间常数。

步骤2-6、利用序列二次规划算法优化高浓磨浆系统运行的经济性能指标函数，获得最优操作变量。

如图18所示，所述步骤2-6，包括：

步骤2-6-1、设定操作变量约束条件、状态变量约束条件、输出的纸浆质量指标游离度约束条件；

操作变量约束：将采集到的螺旋喂料量u₁(kg/min)、磨盘压力u₂(N)、稀释水流量u₃(kg/min)的数据进行分析，选择合适的操作变量约束。

状态变量约束：将采集到的磨机处理量x₁(t/day)、磨机负荷x₂(Mw)、纸浆浓度x₃(％)数据进行分析，选择合适的变量约束。

输出的纸浆质量指标游离度CSF(ml)约束：根据实际工业对纸浆质量工艺指标游离度CSF(ml)要求，设置合理的工艺指标范围。

步骤2-6-2、利用序列二次规划算法优化高浓磨浆系统运行的经济性能指标函数J，所述经济性能指标函数J为能耗目标的加权和控制目标的加权，经济性能指标函数J最小时的操作变量为最优的操作变量。

其中，Q_ζ和Q_u分别为误差加权矩阵和控制权矩阵。P和N分别为状态变量的最大预测长度和控制长度。g(·)为操作变量和状态变量之间的动态关系，f(·)为纸浆质量指标游离度CSF和状态变量之间的非线性关系，l_min和l_max、u_min和u_max、x_min和x_max分别纸浆质量指标游离度CSF、操作变量和状态变量的下限和上限值，α和β分别为实数权值。

本实施方式中N＝10，l_min＝600、l_max＝615、u_min＝[12 900 64]、u_max＝[14 1100 65]、x_min＝[259 8.0 29.5]、x_max＝[263 8.4 32.5]、Q_ξ＝[0.01，0.1，0.01]、Q_u＝[0.05 0.05 0.5]、α＝1、β＝800，利用利用序列二次规划算法优化经济性能指标函数获得最优的操作变量，将获得的最优的螺旋喂料量u₁(kg/min)、磨盘压力u₂(N)、稀释水流量u₃(kg/min)发送至高浓磨浆系统的执行机构，实现高浓磨浆系统经济优化运行和纸浆质量指标游离度CSF的有效控制。

步骤3、将经济性能指标函数最小时的操作变量作为操作变量的最优值，下发到高浓磨浆系统的执行机构，实现高浓磨浆系统经济优化运行和纸浆质量指标游离度的有效控制。

本实施方式获得的状态变量优化结果分别如图8～图16所示。

图8～图10为对应的喂料螺旋转速u₁(kg/min)、磨盘压力u₂(N)、稀释水流量u₃(kg/min)三个操作变量的变化图。

图11～图13为对应的高浓磨浆系统的磨机处理量x₁(t/day)、磨机负荷x₂(Mw)、纸浆浓度x₃(％)的变化图，可以看出状态变量均在约束范围内，且高浓磨系统的纸浆浓度满足实际生产要求。

图14是高浓磨浆系统的比能耗(SE)变化图，可以看出纸浆质量指标的游离度CSF(ml)值越低，比能耗越高，游离度值越高，比能耗越低，这和实际生产过程纸浆质量波动规律符合高浓磨浆系统能耗的变化趋势。

图15是高浓磨浆系统的游离度CSF(ml)输出变化图，可以看出最终输出的纸浆质量工艺指标游离度CSF(ml)的值可以很好的跟踪设定值变化。

图16是高浓磨浆系统的经济性能指标函数变化图，可以看出随着系统运行时间增加，性能指标函数值越来越小，也就是说控制误差越来越小。

本实施方式还提供一种高浓磨浆系统经济优化运行控制系统，如图19所示，包括：

采集单元：采集高浓磨浆系统的螺旋喂料量u₁、磨盘压力u₂、稀释水流量u₃、产量x₁、磨机负荷x₂、纸浆浓度x₃；

操作变量优化单元：利用高浓磨浆系统纸浆质量指标游离度输出模型得到经济性能指标函数最小时的操作变量；高浓磨浆系统纸浆质量指标游离度输出模型的操作变量为螺旋喂料量u₁、磨盘压力u₂、稀释水流量u₃，状态变量为磨机处理量x₁、磨机负荷x₂、纸浆浓度x₃，输出变量为纸浆质量指标游离度CSF(ml)；

运行控制单元：将经济性能指标函数最小时的操作变量作为操作变量的最优值，下发到高浓磨浆系统的执行机构，实现高浓磨浆系统经济优化运行和纸浆质量指标游离度的有效控制。

如图20所示，所述操作变量优化单元，包括：

第一子系统建立模块：采用带控制量自回归模型构建螺旋喂料量u₁与磨机处理量x₁的线性关系模型、磨盘压力u₂与磨机负荷x₂的线性关系模型、稀释水流量u₃与纸浆浓度x₃的线性关系模型，作为一个线性动态子系统；三个线性关系模型的输入变量分别为螺旋喂料量u₁、磨盘压力u₂、稀释水流量u₃；三个线性关系模型的输出变量分别为磨机处理量x₁、磨机负荷x₂、纸浆浓度x₃；

阶次估计模块：采用Hankel矩阵秩估计定阶方法分别估计三个线性关系模型阶次。

参数辨识模块：采用偏差补偿最小二乘递推算法辨识出三个线性关系模型所对应的带控制量自回归模型中的参数；

第二子系统建立模块：将三个线性关系模型的输出变量作为高浓磨浆系统纸浆质量指标游离度输出模型的状态变量，将纸浆质量指标游离度CSF作为输出变量，建立输出变量与状态变量之间的机理模型，作为非线性静态子系统；

模型建立模块：利用线性关系模型和输出变量与状态变量之间的机理模型，建立高浓磨浆系统纸浆质量指标游离度输出模型，高浓磨浆系统纸浆质量指标游离度输出模型即由一个线性动态子系统和一个非线性静态子系统串联的Wiener模型；

操作变量优化模块：利用序列二次规划算法优化高浓磨浆系统运行的经济性能指标函数，获得最优操作变量。

如图21所示，所述操作变量优化模块，包括：

约束条件设定模块：设定操作变量约束条件、状态变量约束条件、输出的纸浆质量指标游离度约束条件；

优化模块：利用序列二次规划算法优化高浓磨浆系统运行的经济性能指标函数，所述经济性能指标函数J为能耗目标的加权和控制目标的加权，经济性能指标函数J最小时的操作变量为最优的操作变量。

其中，Q_ζ和Q_u分别为误差加权矩阵和控制权矩阵。P和N分别为状态变量的最大预测长度和控制长度。g(·)为操作变量和状态变量之间的动态关系，f(·)为纸浆质量指标游离度CSF和状态变量之间的非线性关系，l_min和l_max、u_min和u_max、x_min和x_max分别纸浆质量指标游离度CSF、操作变量和状态变量的下限和上限值，α和β分别为实数权值。