基于TR‑MUSIC算法的光学扫描全息单点定位方法与流程

本发明涉及基于tr-music算法的光学扫描全息单点定位方法。

背景技术：

光学扫描全息技术，简称osh，是数字全息技术的一个重要分支。它利用光学扫描技术将物体的3维信息切片储存为2维信息，从而得到物体的全息图。该技术是1979年，poon和korpel在研究声光外差图像处理器的时候提出。自该技术提出以来，已经在扫描全息显微镜、3d图像识别以及3d光学遥感等领域得到了广泛的应用。

目前光学扫描全息技术实现起来比较复杂，并且在定位的精准上也有所欠缺。

技术实现要素：

本发明要解决的技术问题是：提供基于tr-music算法的光学扫描全息单点定位方法，实现对单个物体的精准定位，并同时提出了将tr-music应用到osh系统中以实现对物体定位的相关理论。

为实现上述目的，本发明采用的技术方案如下：

基于tr-music算法的光学扫描全息单点定位方法，包括以下步骤：

步骤1、将激光采用第一偏振分束器分成两束，之后一束光依次通过第一光瞳和第一凸透镜后投射至第二偏振分束器，第二束光依次通过第二光瞳和第二凸透镜后投射至第二偏振分束器，第二偏振分束器将投射来的两束光聚光干涉形成菲涅尔波带板；

步骤2、首先采用步骤1中获得的菲波对物体进行扫描，然后利用光电探测器接受扫描后的透射光，经过解调后得到物体的切片全息图，最后将全息图采用傅里叶变换后得到矩阵k；

步骤3、通过步骤2中k矩阵得到物体的时间反演矩阵，并求得其特征值和特征向量，从而将全息图分解为信号子空间和噪声子空间；

步骤4、首先利用有限元法将物体等间距离散化，并将各个单元作为测试目标，然后求得各个单元作为测试目标时的全息图，最后利用全息图噪声子空间与信号子空间的正交性得到物体的成像伪谱，最终得到探测目标的位置信息。

进一步地，步骤1中第一光瞳的函数为矩形1函数，第二光瞳的函数为狄拉克δ函数，第一凸透镜和第二凸透镜的焦距相同。

具体地说，步骤1中激光的光学传递函数如下：

将p1(x,y)＝1和p2(x,y)＝δ(x,y)代入式(1)中，则式(1)表示为下式：

则式(2)相应的空间冲击响应为：

其中，j表示虚数单位*表示卷积运算，x'和y'分别表示横向和纵向的积分变量，x表示物体的横向坐标，y表示物体的纵向坐标，z表示2d扫描镜到待测物体的距离，表示波数，λ表示光波波长，f表示凸透镜的焦距，kx和ky表示频域坐标，p1(x,y)和p2(x,y)分别表示第一光瞳和第二光瞳函数。

具体地说，步骤2中所述得到物体切片全息图的关系式如下：

其中，|γ(x,y；z)|²表示物体的复振幅函数，h(x,y；z0)表示扫描位置在z0的点扩散函数，f和f^-1分别表示傅里叶变换和傅里叶反变换，*表示卷积运算。

具体地说，步骤2中所述全息图采用傅里叶变换得到矩阵k的公式如下：

k＝f{hc(x,y；z0)}＝f{|γ(x,y；z0)|²*h(x,y；z0)}(5)

其中，其中x表示物体的横向坐标，y表示物体的纵向坐标，z0表示扫描镜到物体的距离并且此处z0为单值，hc(x,y；z0)表示物体的全息图。

具体地说，步骤3的实现方法如下：

首先将式(5)中求得的矩阵k做奇异值分解即可得时间反演矩阵k^hk和kk^h，具体如下：

k^hk＝f^-1{f{(|γ(x，y；z0)|²)^h*h(x，y；-z0)·f{h(x，y；z0)*(|γ(x，y；z0)|²)}}

＝f^-1{f{(|γ(x，y；z0)|²)^h*h(x，y；-z0)*h(x，y；z0)*(|γ(x，y；z0)|²)}}

其中，h表示矩阵的共轭转置运算，[h(x,y；z0)]^h＝h(x,y；-z0)，并且osh中全息图的重建过程为：

|γ(x,y；z0)|²＝(|γ(x,y；z0)|²)*h(x,y；z0)*h(x,y；-z0)(7)

因此，可以得到时间反演矩阵k^hk和kk^h如下：

k^hk＝(|γ(x,y；z0)|²)^h*|γ(x,y；z0)|²

kk^h＝|γ(x,y；z0)|²*(|γ(x,y；z0)|²)^h(8)

然后，求得时间反演阵k^hk和kk^h的特征值λ和特征向量v1、v2，非零特征值对应的特征向量对应信号子空间，其余的对应噪声子空间；由式(8)可知，v1携带了物体y方向的特征信息，v2携带了物体x方向的特征信息，其中信号子空间与噪声子空间相互正交，具体如下：

＜v1(i＝1,...m),v1(j＝m+1,...n)＞＝0

＜v2(i＝1,...m),v2(j＝m+1,...n)＞＝0

其中，m≤n且m＝1，m表示非零特征值的个数，n表示特征值的总个数。

具体地说，步骤4中利用全息图噪声子空间与信号子空间的正交性得到物体成像伪谱的方法如下：

用v2中噪声子空间对应的特征向量的共轭转置左乘测试目标的全息图ki(xp)并求和得qx(xp)，用v1中噪声子空间对应的特征向量右乘测试目标的全息图ki(xp)并求和qy(xp)，即：

其中，xp为各个单元测试目标，并且xp为n×n个点，ki(xp)为各个单元测试目标xp通过式(4)求得的全息图，i＝1,2,3...n²，m表示向量|ki(xp)v1(j)|²或|v2(j)ki(xp)|²第m个元素，j表示v1(j)或v2(j)的第j个特征向量，m≤n且m＝1，m表示非零特征值的个数，n表示特征值的总个数，qx(xp)和qy(xp)表示x和y方向测试目标xp伪谱的一个中间值。

当测试目标在探测目标的位置时，qx(xp)和qy(xp)约等于0，而测试目标不在探测目标位置时，qx(xp)和qy(xp)的值有限，在求得测试目标xp的qx(xp)和qy(xp)之后，即可求得该点的x方向和y方向的成像伪谱px(xp)和py(xp)，具体为：

px(xp)＝||ki(xp)||²/qx(xp)

py(xp)＝||ki(xp)||²/qy(xp)(10)

其中，px(xp)和py(xp)分别表示探测目标在x和y方向上的成像伪谱，式(10)中的px(xp)和py(xp)相乘可以得到测试目标xp的成像伪谱p(xp)，具体为：

p(xp)＝px(xp)py(xp)(11)

当逐点求得p(xp)之后，可以得到包含探测目标位置信息的成像伪谱，最终通过成像伪谱得到探测目标的精准位置。

具体地说，步骤4中利用全息图噪声子空间与信号子空间的正交性得到物体成像伪谱的方法如下：

首先，对测试目标xp的全息图ki(xp)做奇异值分解，即求得ki(xp)时间反演阵[ki(xp)]^hki(xp)及ki(xp)[ki(xp)]^h的非零特征值对应的特征向量vy和vx；

然后，通过下式求得测试目标xp的qx(xp)和qy(xp)，具体为：

其中，*表示共轭，t表示矩阵的转置运算，当测试目标在探测目标的位置时，qx(xp)和qy(xp)约等于0，而测试目标不在探测目标位置时，qx(xp)和qy(xp)的值有限；

最后，通过下式就可求得测试目标xp的成像伪谱p(xp)，最终通过成像伪谱得到探测目标的精准位置，具体为：

px(xp)＝||vx||²/qx(xp)

py(xp)＝||vy||²/qy(xp)

p(xp)＝px(xp)py(xp)(13)

其中px(xp)和py(xp)分别表示探测目标在x和y方向上的成像伪谱，p(xp)表示包含探测目标位置信息的成像伪谱。

与现有技术相比，本发明具有以下有益效果：

(1)本发明首创性的使用tr-music算法对全息图进行处理，从而获得物体中探测目标的准确位置。

(2)本发明使用tr-music算法实现对探测目标的定位，具有较高的精度与定位的准确性。

(3)本发明针对tr-music算法，利用物体噪声子空间与信号子空间的正交性得到物体的成像伪谱，给出了两种可行方案，并说明了两种方法的关系。给出了在全息扫描技术下使用tr-music算法实现定位的相关公式，即式(1)-式(13)，建立了本发明的理论基础。

(4)本发明不仅实现方式简单、便于操作，同时具有很强的实用性，适合推广使用。

附图说明

图1为本发明流程示意图。

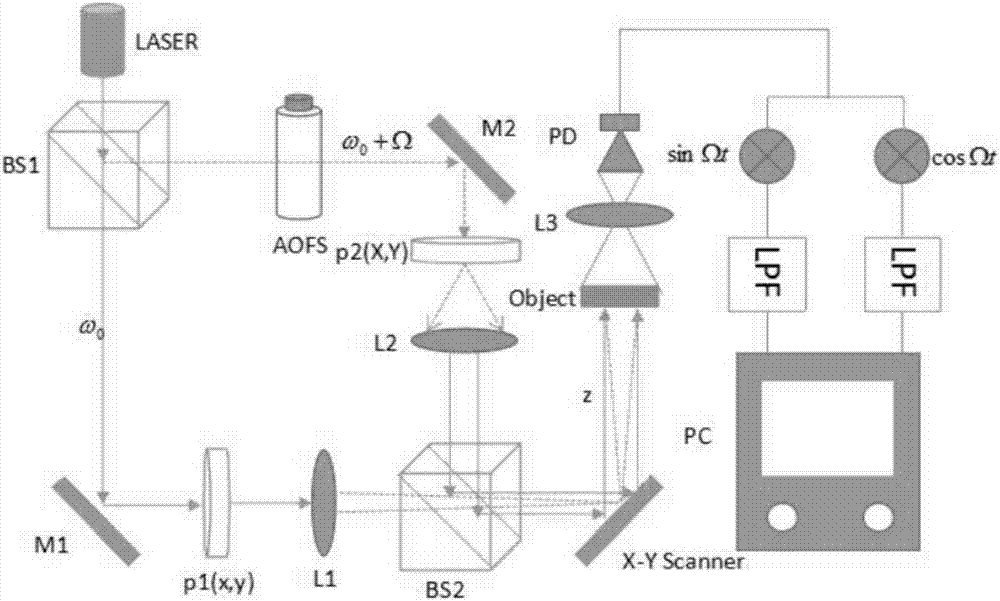
图2为本发明实施例采用的基本结构图。

图3为本发明实施例采用的探测目标位置示意图。

图4为本发明实施例的奇异值分解后，其特征值分布图。

图5为本发明实施例最终得到的成像伪谱。

具体实施方式

下面结合附图说明和实施例对本发明作进一步说明，本发明的方式包括但不仅限于以下实施例。

实施例

如图1，本发明提供的基于tr-music算法的光学扫描全息单点定位方法，采用tr-music算法对全息图进行处理，从而实现对探测目标的定位，具有较高的精度并且定位相当准确；本基于tr-music算法的光学扫描全息单点定位方法不仅实现方式简单、便于操作，同时具有很强的实用性，适合推广使用。

本基于tr-music算法的光学扫描全息单点定位方法采用如图2所示的结构来实现，该结构具体包括第一偏振分束器bs1、第二偏振分束器bs2、第一光瞳p1(x,y)、第二光瞳p2(x,y)、第一凸透镜l1、第二凸透镜l2、第三凸透镜l3、声光调制器aofs、第一反射镜m1、第二反射镜m2、扫描器x-yscanner、光电二极管pd、光电振荡器、两个lpf、以及pc机。激光光源发射的激光通过第一偏振分束器bs1后分成两束光，其中一束光依次通过第一反射镜、第一光瞳和第一凸透镜射入第二偏振分束器bs2，另一束光依次通过声光调制器、第二反射镜、第二光瞳和第二凸透镜射入第二偏振分束器bs2，两束光经过第二偏振分束器bs2聚合后干涉形成菲涅尔波带板并投入扫描器，扫描器将上述菲涅尔波带板对被测物体(object)进行扫描，扫描后的透射光通过第三透镜后经过光电二极管转化成电信号并经过光电振荡器后分别经过两个lpf传输至pc机。

本实施例所采用的结构中he-ne激光器laser的波长λ＝632.8nm，两个凸透镜(l1、l2)的焦距都为400mm，扫描镜到物体的距离为z＝400mm，物体如图3所示放置，物体采用的切片尺寸为8mm×8mm，物体经有限元法离散后的阵列为16×16，探测目标放在坐标为(10,5)处。

本基于tr-music算法的光学扫描全息单点定位方法的具体步骤为：

步骤1、得到菲涅尔波带板。

如图2所示，由同一激光光源发出的角频率为ω的光被第一偏振分束器bs1分成两束，其中一束通过第一光瞳p1(x,y)形成平面波；另一束经过声光调制器产生ω的频移后再通过第二光瞳p2(x,y)形成球面波；两束光经第二偏振分束器bs2聚合后在待测物体前干涉形成菲涅尔波带板，其可以由式(3)得到，具体为：

首先，激光光源发出的激光经过第一偏振分束器bs1分束，再分别经过第一光瞳p1(x,y)和第二光瞳p2(x,y)后通过第二偏振分束器聚合后在待测物体前干涉形成菲涅尔波带板的光学传递函数为：

本实施例中第一光瞳的函数为矩形1函数，第二光瞳的函数为狄拉克δ函数，并且在第一光瞳和第二偏振分束器之间设有第一凸透镜，在第二光瞳和第二偏振分束器之间设有第二凸透镜，且第一凸透镜和第二凸透镜的焦距相同，于是，将p1(x,y)＝1和p2(x,y)＝δ(x,y)代入式(1)中，则式(1)表示如下：

则式(2)相应的空间冲击响应即为下式：

其中，x表示物体的横向坐标，y表示物体的纵向坐标，z表示2d扫描镜到待测物体的距离，表示波数，λ表示光波波长，f表示两个凸透镜的焦距，kx和ky表示频域坐标，p1(x,y)和p2(x,y)分别表示第一光瞳和第二光瞳函数。

步骤2、用菲涅尔波带板扫描物体，得到物体的全息图。

首先采用步骤1中获得的菲涅尔波带板对物体进行扫描，然后利用光电探测器接受扫描后的透射光，经过解调后得到物体的切片全息图，最后将全息图采用傅里叶变换后得到矩阵k

为得到物体的全息图，可使用：

又根据物体的全息图hc(x,y；z0)得到矩阵k，

k＝f{hc(x,y；z0)}＝f{|γ(x,y；z0)|²*h(x,y；z0)}(5)

其中，x表示物体的横向坐标，y表示物体的纵向坐标，z0表示扫描镜到物体的距离(此处z0为单值)，hc(x,y；z0)表示物体的全息图。

步骤3、通过矩阵k得到物体的时间反演矩阵，并求得其特征值和特征向量，从而将全息图分解为信号子空间和噪声子空间。

首先，对矩阵k做奇异值分解，根据式(5)可以求得矩阵k，进而求得时间反演矩阵k^hk和kk^h，具体为：

k^hk＝f^-1{f{(|γ(x，y；z0)|²)^h*h(x，y；-z0)·f{h(x，y；z0)*(|γ(x，y；z0)|²)}}

＝f^-1{f{(|γ(x，y；z0)|²)^h*h(x，y；-z0)*h(x，y；z0)*(|γ(x，y；z0)|²)}}

其中，h表示矩阵的共轭转置运算，[h(x,y；z0)]^h＝h(x,y；-z0)，并且osh中全息图的重建过程为：

|γ(x,y；z0)|²＝(|γ(x,y；z0)|²)*h(x,y；z0)*h(x,y；-z0)(7)

因此，可以得到时间反演矩阵k^hk和kk^h如下：

k^hk＝(|γ(x,y；z0)|²)^h*|γ(x,y；z0)|²

kk^h＝|γ(x,y；z0)|²*(|γ(x,y；z0)|²)^h(8)

然后，求得时间反演阵k^hk和kk^h的特征值λ和特征向量v1、v2，非零特征值对应的特征向量对应信号子空间，其余的对应噪声子空间，如图4所示；且由式(8)可知，v1携带了物体y方向的特征信息，v2携带了物体x方向的特征信息。其中信号子空间与噪声子空间相互正交：

＜v1(i＝1,...m),v1(j＝m+1,...n)＞＝0

＜v2(i＝1,...m),v2(j＝m+1,...n)＞＝0

其中，m(m≤n且此处m＝1)表示非零特征值的个数，也即是探测目标的个数，n表示特征值的总个数。

步骤4、利用有限元法将物体等间距离散化，并将各个单元作为测试目标；然后求得各个单元作为测试目标xp(xp为16×16个点)，并通过式(4)可以求得测试目标xp的全息图ki(xp)(i＝1,2,3...n²)。

最后，利用物体噪声子空间与信号子空间的正交性得到物体的成像伪谱，如图5所示，并与图3放置的物品位置相吻合。为了得到物体的成像伪谱，本实施例提供了两种相关联的方法，具体如下：

方法1：用v2中噪声子空间对应的特征向量的共轭转置左乘ki(xp)并求和得qx(xp)，用v1中噪声子空间对应的特征向量右乘ki(xp)并求和qy(xp)，即如下式所示：

当测试目标在探测目标的位置时，qx(xp)和qy(xp)约等于0，而测试目标不在探测目标位置时，qx(xp)和qy(xp)的值有限。求得测试目标xp的qx(xp)和qy(xp)之后，即可求得该点的x方向和y方向的成像伪谱px(xp)和py(xp)为：

px(xp)＝||ki(xp)||²/qx(xp)

py(xp)＝||ki(xp)²/qy(xp)(10)

其中px(xp)和py(xp)分别表示探测目标在x和y方向上的成像伪谱，式(10)中的px(xp)和py(xp)相乘可以得到测试目标xp的成像伪谱：

p(xp)＝px(xp)py(xp)(11)

当逐点求得p(xp)之后，可以得到包含探测目标位置信息的成像伪谱，最终，通过成像伪谱得到探测目标的位置。

方法2：首先，对测试目标xp的全息图ki(xp)做奇异值分解，即求得ki(xp)时间反演阵[ki(xp)]^hki(xp)及ki(xp)[ki(xp)]^h的非零特征值对应的特征向量vy和vx。然后通过式(12)求得测试目标xp的qx和qy，即：

其中，*表示共轭。当测试目标在探测目标的位置时，qx(xp)和qy(xp)约等于0，而测试目标不在探测目标位置时，qx(xp)和qy(xp)的值有限。最后，通过下式即可求得测试目标xp的成像伪谱p(xp)，即：

px(xp)＝||vx||²/qx(xp)

py(xp)＝||vy||²/qy(xp)

p(xp)＝px(xp)py(xp)(13)

其中px(xp)和py(xp)分别表示探测目标在x和y方向上的成像伪谱，p(xp)表示包含探测目标位置信息的成像伪谱。

值得注意的是，在步骤4中，利用物体噪声子空间与信号子空间的正交性得到物体的成像伪谱的两种方法是有关联性的，具体分析如下：

对于步骤3和步骤4的过程可以看作是对矩阵k做奇异值分解的过程，因此，有从而有而对应的而对于＜v2(j＝m+1,...,n),vx＞≈0，＜v1(j＝m+1,...,n),vy＞≈0。因此

其中c表示常数，y方向同理。从式(14)知道方法1和方法2之间相差一个常数的倍数关系，而这并不影响对探测目标位置的确定。

本发明首创性的使用tr-music算法对全息图进行处理，从而实现对探测目标的定位，具有较高的精度并且定位相当准确；同时，本发明针对tr-music算法，利用物体噪声子空间与信号子空间的正交性得到物体的成像伪谱，给出了两种可行方案，并说明了两种方法的关系。并且首创性的给出了在全息扫描技术下使用tr-music算法实现定位的相关公式，即式(1)-式(13)，建立了本发明的理论基础，具备凸出的实质性特点和显著进步。本发明不仅实现方式简单、操作便捷，同时具有很强的实用性，适合推广使用。

上述实施例仅为本发明的优选实施方式之一，不应当用于限制本发明的保护范围，但凡在本发明的主体设计思想和精神上作出的毫无实质意义的改动或润色，其所解决的技术问题仍然与本发明一致的，均应当包含在本发明的保护范围之内。