基于振幅空间光调制器的非瑞利统计分布散斑场生成方法与流程

本发明涉及一种基于二值振幅型空间光调制器件实现非瑞利散斑复数场的调制方法，属于特殊光场调制领域。

背景技术：

通常自然界中见到的散斑场振幅服从瑞利统计分布，强度服从复指数分布，我们发明了一种利用纯振幅型空间光调制器件生成非瑞利散斑场的方法。纯振幅型空间光调制器相较于液晶型空间光调制器最大的优势在于它的高速性，而且纯振幅型空间光调制器的调制效率高，鲁棒性强。最近，非瑞利分布散斑场在很多领域都引起了科研工作者们很多的关注，诸如动态散斑照明显微成像，光学超分辨率成像，基于赝热光源的高阶鬼成像等领域。

通常生成非瑞利统计分布散斑场的方法是利用液晶型空间光调制器(slm)配合单个透镜实现的。在这种方法中，首先要进行强度转换的操作，即由瑞利统计分布散斑场的强度出发，根据求解概率密度函数的不定积分式可以得出由瑞利统计分布散斑场到非瑞利统计分布散斑场的强度转换公式。计算得出非瑞利统计分布散斑场强度之后需要根据强度分布利用类g-s相位恢复算法计算需要加载到液晶型空间光调制器上的相位分布，使得该相位场经过透镜进行傅里叶变换后能得到目标非瑞利分布散斑强度场。在这个过程中，无法控制非瑞利统计分布散斑场的相位分布，计算过程非常复杂且耗时，其调制频率也受限于液晶型空间光调制器的调制频率，一般只能达到60hz，大大限制了基于非瑞利统计分布散斑场相关应用的拓展。

技术实现要素：

本发明的目的在于，提供一种基于振幅空间光调制器的非瑞利统计分布散斑场生成方法，该方法利用二值振幅型空间光调制器实现直接对非瑞利统计分布散斑复数场振幅和相位的调制，以提高基于非瑞利统计分布散斑场的相关应用的效率。

本发明基于振幅空间光调制器的非瑞利统计分布散斑场生成方法，包括振幅和相位调制以及非瑞利散斑场计算两个部分：

振幅和相位调制是将空间光调制器表面的3×3或者4×4个像素组合为一个超像素，通过控制一个超像素内不同像素的亮暗组合，配合离轴的4-f系统和放置在4-f系统频谱面的低通滤波器，滤出特定空间位置处的频谱，在4-f系统后焦面上实现对不同振幅和相位的调制；

非瑞利散斑场计算：通常对振幅为1，相位在0到2π均匀分布的随机相位场做傅里叶变化得到散斑场，散斑场的振幅服从瑞利统计分布，强度服从复指数分布，得到振幅服从非瑞利统计分布的散斑场，不断进行低通滤波操作，对滤波后的散斑复数场再次进行强度转换操作，不断迭代上述过程，直到目标非瑞利统计分布散斑场的频谱范围满足要求，且强度服从目标统计分布。

所述振幅和相位调制的具体过程如下所述：

(1)将振幅型空间光调制器平面4×4个像素人为的组合为一个超像素，通过分别控制一个超像素内的16个像素的两种状态，在目标平面调控出复数值(可调控出六千多种复数值)。

(2)离轴的4-f系统使得空间光调制器平面每个像素的出射光在目标平面上的响应有固定的相位差，在横向上有的相位差，在纵向上有的相位差。其中n为超像素的分辨率大小(实验中选取n＝4)，d为空间光调制器每个像素的大小。

(3)通过设计4-f系统中间频谱面低通滤波窗的位置(特定空间位置处)和大小，引入相位差和平滑一个超像素内的单个像素，使得4×4个像素模糊化为一个超像素。

(4)通过选取一个超像素内不同像素的状态组合(即选择每个像素的“开”和“关”两种状态组合)，生成一个查找表，查找表中每个复数值对应一种状态组合，表示采用该状态组合通过上述方法的调制后能生成该复数值对应的光场。

(5)针对每一种复数光场，通过每个像素点的复数值查询查找表中对应的像素状态组合，即可得到空间光调制器每个像素需要调制的状态。

所述述非瑞利统计分布散斑场的计算过程如下所述：

(1)用振幅为1，相位在0到2π均匀分布的纯随机相位场做傅里叶变换，得到振幅服从瑞利统计分布，强度服从复指数分布的瑞利散斑复数场。

(2)将瑞利散斑场的强度做强度转化，得到强度服从目标统计分布的散斑场。

(3)将振幅转换，相位保持不变的散斑复数场做低通滤波，滤波窗的大小和上述基于振幅型空间光调制器的振幅和相位调制过程中滤波窗口大小一致。

(4)低通滤波后的复数场强度的统计分布会偏离目标概率密度分布，需要再对滤波后的复数场进行强度转换和低通滤波操作，重复步骤(1)-(3)，直到低通滤波后的散斑场强度满足目标统计分布为止。

本发明利用二值型纯振幅空间光调制器配合相关实验设备生成不同统计分布的非瑞利统计分布散斑场，其调制速度可达22.7khz，大大提高了基于非瑞利统计分布散斑场的相关应用的效率。采用基于超像素的方法，调至精度可达到98％以上。且可以同时实现散斑复数场的振幅和相位调制，在对散斑的相关特性研究中具有一定的价值。

附图说明

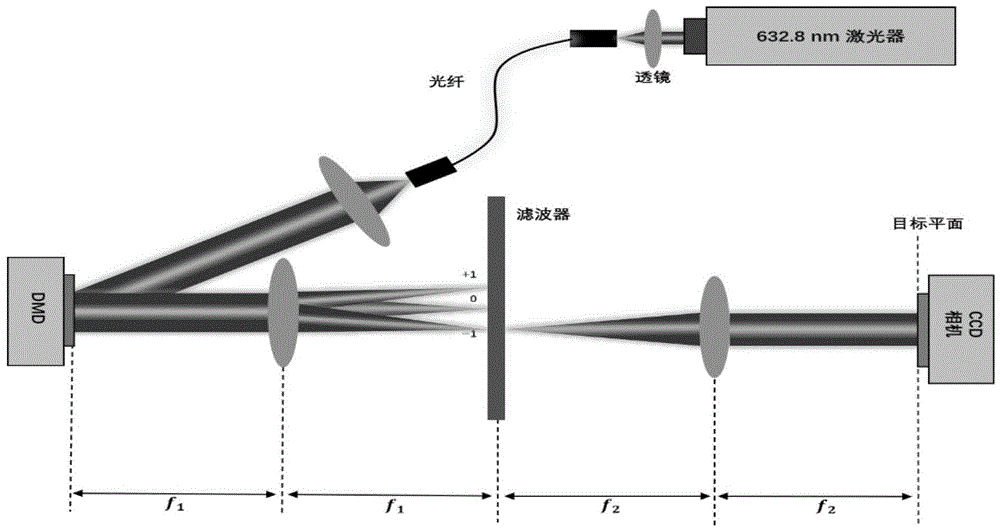
图1是基于二值振幅型空间光调制器的复光场调制实验装置图。

图2是目标散斑复数场和基于超像素方法采用二值振幅型空间光调制器生成的散斑复数场，其归一化相关系数高达0.983。

图3是计算生成非瑞利统计分布散斑复数场的算法流程图。

图4是振幅服从瑞利统计分布，强度服从复指数分布的散斑场。

图5是三种非瑞利统计分布散斑场的实验结果图，分别为强度服从均匀分布，线性分布和正弦函数分布的散斑强度场，及其各自强度的统计分布曲线。

具体实施方式

首先介绍基于超像素的复振幅光场调制技术原理，是基于超像素的原理，即将空间光调制器表面的3×3或者4×4个像素组合为一个超像素，通过控制一个超像素内不同像素的亮暗组合，配合离轴的4-f系统和放置在4-f系统频谱面的低通滤波器，滤出特定空间位置处的频谱，即可在4-f系统后焦面上实现对不同振幅和相位的调制。

具体的实验装置如图1所示，波长为632.8nm的氦氖激光器出射光束通过单模光纤和透镜扩束准直，得到的平行光以特定的角度(与空间光调制器靶面对角线成24°)照射dmd调制靶面，在dmd靶面进行二值振幅调制。其中每个像素大小为13.68um，二值振幅型空间光调制器的调制靶面由1024×768个微反射镜组成，每个微反射镜有两种状态：“开”和“关”，分别对应对光场进行“1”和“0”的两种振幅调控状态。调制后的光束垂直空间光调制器调制靶面出射，经过一个离轴的4-f系统，并在4-f系统频谱面进行特定空间位置处的滤波，选择合适的滤波窗大小和位置(特定空间位置)，在4-f系统后焦面处即可得到由空间光调制器靶面调制出的目标光场。具体原理如下：

(1)空间光调制器出射光场用c(x，y)表示，经过4-f系统的第一个透镜后(相当于对c(x，y)进行一次傅里叶变换)，得到4-f系统频谱面的光场分布，用c(wx，wy)表示。

(2)在4-f系统频谱面进行低通滤波，滤波窗空间位置为其中λ为波长，f2为4-f系统第二个透镜的焦距，n为超像素的分辨率大小(实验中选4×4个像素组合为一个超像素，即n＝4)，d为空间光调制器靶面单个像素大小。

(3)由于4-f系统离轴放置，其中第二个透镜与滤波小孔同轴放置，相当于第一个透镜后焦面的光场相对于第二个透镜做了一个的频移，小孔的函数用

表示。

(4)对于第二个透镜来说，前焦面的入射光场为经过第二个透镜以后(即进行一次傅里叶变换)，得到后焦面(即目标平面)的出射光场，用表示。其中为滤波小孔函数的傅里叶变换形式,j1(ρ)为一阶贝塞尔函数，且“*”表示卷积操作。

(5)空间光调制器调制靶面被分割成一个个的超像素，每个超像素由n×n个小像素组成，滤波器滤除了高频成分，使用使得单个小像素模糊化为一个像素。空间光调制器靶面的每个超像素对应目标平面的一个像素，目标平面上每个像素处的振幅和相位也因此由空间光调制器靶面的超像素单独调控。

(6)用归一化相关系数表示该方法的调制精度，根据模拟和实验结果分析，调制精度可达98％以上。图2表示目标散斑复数场和基于超像素方法采用二值振幅型空间光调制器生成的散斑复数场的强度和相位分布图。用归一化相关系数衡量调制精度，其归一化相关系数为0.983。归一化相关系数表达式如下：

由于离轴放置的4-f系统引入的相位差，通过控制这n×n个像素的开关组合，可在目标平面调制出多种复数场，实现由光场的二值振幅调制到复数光场调制的功能。基于该实验装置生成非瑞利统计分布散斑场的方法相较于用液晶型空间光调制器生成的方法调制速度快、精度高，且计算过程简单，在调制强度统计分布的同时还可以同时实现对相位的调制。

以下再介绍可定制统计分布的非瑞利散斑复数场的生成步骤，通常对振幅为1，相位在0到2π均匀分布的随机相位场做傅里叶变化即可得到散斑场，该种散斑场的振幅服从瑞利统计分布，强度服从复指数分布(如图1)，强度复指数分布的特性也作为散斑完备性的衡量标准之一。为了得到振幅服从非瑞利统计分布的散斑场，如振幅服从均匀分布，线性分布，sin函数分布等的散斑场，需要一系列的操作从瑞利分布散斑场出发，通过强度转换和低通滤波操作得到。由于采用的基于超像素的方法，该方法对目标场的频谱范围有一定的限制，所以计算生成非瑞利统计分布散斑场的过程中需要考虑到这一因素，在计算过程中的需要不断进行低通滤波操作，又由于低通滤波会使得滤波后的复数场的振幅偏离目标统计分布，所以又需要对滤波后的散斑复数场再次进行强度转换操作，不断迭代上述过程，直到目标非瑞利统计分布散斑场的频谱范围满足要求，且强度服从目标统计分布。图3详细说明了由瑞利统计分布散斑复数场到非瑞利统计分布散斑复数场的转换过程。

(1)瑞利统计分布散斑场可由振幅为1，相位在0到2π均匀分布的纯随机相位场模拟，即其中表示傅里叶变换，sizex，sizey为初始瑞利

统计分布散斑场的分辨率。图4为振幅服从瑞利统计分布的散斑强度场，其强度服从复指数分布。其中红线表示标准的复指数分布，黑色实线表示左边散斑强度的统计分布。

(2)假定目标统计分布散斑场强度概率密度函数用表示，根据不定积分式：

求解得出和i之间的强度转换关系。其中p表示瑞利统计分布散斑场的概率密度函数，imin和为散斑场最小强度，一般均设为0。

(3)对强度转换后的复数场进行低通滤波操作，得到强度统计分布偏离目标统计分布的复数场，再计算该复数场强度的概率密度函数，用p′(i)表示。再根据步骤(2)中的不定积分式重新计算和i之间的强度转换关系式。

(4)重复步骤(2)和(3)，直到低通滤波后的复数场满足目标统计分布。此时的复数场即为目标统计分布散斑复数场，可用上述基于振幅型空间光调制器配合离轴的4-f系统的方法生成。图5为实验生成的强度服从均匀分布，线性分布和正弦函数分布的散斑强度场和各自的强度统计分布曲线。其中红色实线表示理论统计分布，黑色实现表示实际试验系统生成散斑的强度统计分布曲线。