一种用于定制照明的全内反射透镜设计方法与流程

本发明属于光学透镜技术领域，具体涉及一种用于定制照明的全内反射透镜设计方法。

背景技术：

近年来，各领域对于照明提出了更高的要求，例如要求led在复杂形状的目标面上产生均匀、高效的辐照分布，使其能够满足弯曲道路的照明，同时又要兼顾道路周边环境中较低层次的照明；又例如在机器视觉中，要求光源能够在目标面上的不同区域生成不同层次的辐照度，从而抑制由于目标表面的光学特性、特殊结构而引发高光、阴影等现象。上述需求对于led配光技术具有一定的挑战性；目前常用led配光元件主要包括led阵列、配光透镜和配光反射镜等。其中led配光透镜的种类较多，其面型多为非球面、自由曲面或全内反射透镜；其中非球面配光透镜只能在目标面上生成圆形的均匀光斑，难以定制光斑的形状，而自由曲面透镜设计方案可以在一定程度地解决上述问题，例如花生透镜，作为一种成熟的自由曲面透镜，其可在目标面上生成均匀的矩形光斑。然而，该透镜并不能生成任意形状的均匀光斑，且难以在目标面上生成不同层次的辐照度。全内反射透镜具有更高的光能利用率和优秀的配光特性，但现有的全内反射透镜大多为旋转对称形，多用于简单的准直或产生均匀的圆形光斑，其同样无法满足定制照明的复杂需求。因此，基于全内反射透镜高效率、配光性能优良的优点，开发一种新型全内反射透镜的设计方法，使其能够在目标面上生成不同形状的高效率、均匀光斑，且光斑包含两种具有不同辐照度的区域，具有一定的现实意义。

技术实现要素：

本发明的目的在于提供一种用于定制照明的新型全内反射透镜设计方法，旨在目标面上生成多种形状的高效率均匀照明光斑，且光斑包含两种具有不同辐照度的区域，

本发明提供的用于定制照明的全内反射透镜设计方法，是基于snell定律和边缘光线理论，结合能量守恒定律，建立全内反射非球面型的数学模型和和透射非球面的数学模型，得到两组微分代数方程表示两种非球面的轮廓曲线，并采用龙格库塔法进行求解得出非球面面型数据；定制光斑的图案由透镜边界形状决定，将定制光斑的辐照度分布问题转化为自由曲面面型求解问题，建立一组非线性方程，通过求解该非线性方程得到透镜边界自由曲面轮廓，利用商用cad工具所得非球面与自由曲面组合为一个透镜；将边界自由曲面处理为漫透射结构，可以提高能量利用率。具体步骤如下：

(1)构建全内反射透镜数学模型

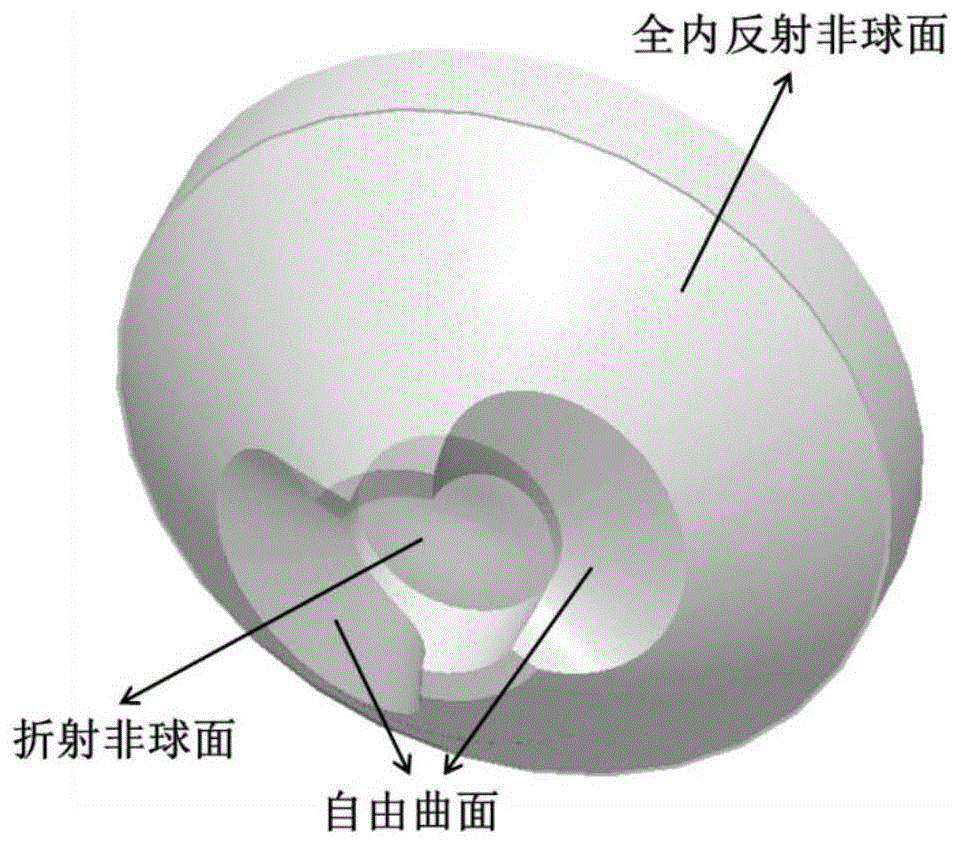
将所需设计的全内反射透镜置于led和目标面之间，基于所选led的光强分布，在笛卡尔坐标系中建立全内反射透镜数学模型，参见图1所示；该模型由三部分组成，即折射非球面模型、全内反射非球面模型和自由曲面模型；

(2)求解折射非球面；

首先确定led光线经折射非球面调控后在目标面产生的均匀光斑半径rmax、照射距离l、透镜折射率n、透镜中心厚度d、led最大出射半角θmax以及led与透镜中心距离h这些条件，设折射非球面上任意点的横坐标为x，纵坐标为ysurface；根据折射非球面的光通量守恒定律，有：

其中，e(y)表示目标面上某点所接收的光通量,y表示该点的纵坐标，θ表示led出射角度.根据照度均匀原则，目标平面内每一点的照度应相等，则公式(1)转换为：

其中，e0表示目标面上的均匀照度值，推导公式(2)得：

e0＝iaxis·sin²θ1/rmax²(3)

其中，iaxis表示led的轴向光强，θ1为折射非球面与全内反射非球面的临界角，联立公式(1)和公式(3)得：

公式(4)表示y和θ之间的关系；

再根据光斑定制区域与背景区域的辐照度比值，计算折射非球面与全内反射非球面的临界角θ1，具体表示为：

其中，b表示光斑定制区域与背景区域的辐照度比值；

根据snell定律，折射非球面上每一点斜率dysurface/dx表示为：

dysurface/dx＝(n·cosμ-cosθ)/(sinθ-n·sinμ)(6)

μ为折射非球面出射光线与光轴之间的夹角；此时又根据led与折射非球面的几何关系，ysurface和x之间又遵循如下关系：

ysurface＝(d+h+x)·tanθ(7)

公式(7)两边分别对θ进行微分得：

联立公式(6)和公式(8)，得微分方程f1，用以表示dx/dθ、x和θ之间的数学关系；

再根据公式(4)，有：

y＝rmax·sinθ/sinθ1(10)

根据led与折射非球面的几何关系，又得：

联立公式(10)和公式(11)，得到一个非线性方程f2＝0，具体为：

联立公式(9)和公式(12)，得到一组微分代数方程该方程组的数值解即为构成折射非球面离散点坐标；

(3)求解全内反射非球面：

参考求解折射非球面的步骤，在确定由全内反射非球面调控均匀光斑半径r′max和折射非球面最大半径h后，基于led与全内反射非球面的几何关系和snell定律，推导得出一个微分方程f3，具体为：

公式(13)为一个微分方程，其表示全内反射非球面各点横坐标x′和led出射角θ′、dx′/dθ′之间的数学关系，其中f3＝dx′/dθ′，再根据光通量守恒，照度均匀原则以及led与全内反射非球面的几何关系，得到全内反射非球面各点纵坐标y′surface与全内反射非球面出射光线与光轴之间的夹角μ′、x′、θ′之间的数学关系f4，具体为：

联立公式(13)和公式(14)，得到一组微分代数方程该方程组的数值解即为构成全内反射非球面离散点坐标；

(4)求解微分代数方程组和微分代数方程组

利用数学软件，采用runge-kutta法分别求解微分代数方程组和微分代数方程组的数值解，求解范围分别为[0,θ1]和(θ1,θmax]，得到两组离散点的坐标，分别为折射非球面离散点坐标和全内反射非球面离散点坐标；利用最小二乘法将两组离散点坐标各自拟合成平滑的二维曲线，其中离散点的数量决定二维曲线的精度；

再将所得二维曲线导入至solidworks制图软件，绕光轴旋转一周得到一个旋转对称形透镜；

(5)求解自由曲面

对于不同形状的定制光斑，首先确定光斑定制区域边界在笛卡尔坐标系中坐标(xd,yd)，再将其转换为极坐标(r,β)，其中r即光斑定制区域在不同方向的横截面上的边界位置，β∈[0,2π]表示方向，以定制矩形光斑为例，将其矩形边界各点的笛卡尔坐标转换为极坐标(rp,βp)，并以此为边界条件，再根据led与全内反射非球面的几何关系和snell定律，得到自由曲面在任意方向的横截线段x″＝xp的表达式：

结合光通量守恒公式，θp表示为：

联立公式(15)和公式(16)，求解得出自由曲面在各方向上的横截线段，将其导入至solidworks制图软件，通过闭合放样得到一个自由曲面，其中横截线段数量越大，所得自由曲面的面型精度越高；

(6)设计新型全内反射透镜

将步骤(5)所得自由曲面与步骤(4)所得的透镜导入solidworks2012制图软件，通过布尔运算进行组合，即构成本发明所设计的新型全内反射透镜。

将边界自由曲面处理为漫透射结构，可以提高能量利用率。

本发明中，所述的led发光特性为朗伯体，且led发光面的尺寸相对于新型全内反射透镜尺寸应越小越好。所述的新型全内反射透镜材质可为任意已知折射率n的高透光材质。

本发明设计的光学器件具有良好的配光性能，其可以定制照明光斑的形状，且包含两种具有不同辐照度的区域，分别为光斑定制区域和背景区域，辐照均匀性良好，其光斑定制区域的辐照均匀度达到95.3％，背景区域的辐照均匀度达到89.3％，同时led能量利用率为89.3％，因此本发明具有较高的能量利用率，具有节能的优点，克服了传统全内反射透镜无法在目标面上产生定制形状的、且包含两种辐照度的、高效率均匀照明光斑的不足。

附图说明

图1为本发明所述的新型全内反射透镜示意图。

图2为本发明所述的折射非球面结构示意图。

图3为本发明所述的全内反射非球面结构示意图。

图4为本发明中辐照度比值为2:1的矩形定制透镜示意图及其辐照分布图。

图5为本发明中辐照度比值为2:1的曲形定制透镜示意图及其辐照分布图。

图6为本发明中辐照度比值为5:1的矩形定制透镜示意图及其辐照分布图。

具体实施方式

下面通过具体实施例进一步介绍本发明。

(1)折射非球面结构示意图如图2所示，首先根据设计需求确定led光线经折射非球面调控后在目标面产生的均匀光斑半径rmax＝1000mm、照射距离l＝1000mm、透镜折射率n＝1.643、透镜中心厚度d＝10mm、led最大出射半角θmax＝π/2rad以及led与透镜中心距离h＝5mm等条件，设待求解的折射非球面任意点的横坐标为x，纵坐标为ysurface，基于led与折射非球面的几何关系、光通量守恒公式和snell定律，推导得出一组daes，具体过程为：

根据折射非球面的光通量守恒可得：

其中，e(y)表示目标面上某点所接收的光通量,y表示该点的纵坐标，θ表示led出射角度.根据照度均匀原则，目标平面内每一点的照度应相等，则公式(1)可转换为：

其，中e0表示目标面上均匀照度值，此时，根据公式(2)可得：

e0＝iaxis·sin²θ1/rmax²(3)

其中，iaxis表示led的轴向光强，联立公式(1)和公式(3)，则可得y和θ之间的关系：

再根据设计需求中光斑定制区域与光斑背景区域的辐照度比值，计算折射非球面与全内反射非球面的临界角θ1，具体可表示为：

其中，b表示光斑定制区域与光斑背景区域的辐照度比值，本发明以b＝2:1为例；根据snell定律，折射非球面上每一点斜率dysurface/dx可表示为

dysurface/dx＝(n·cosμ-cosθ)/(sinθ-n·sinμ)(6)

此时又根据led与折射非球面的几何关系，ysurface和x之间又遵循如下几何关系：

ysurface＝(d+h+x)·tanθ(7)

公式(7)两边分别对θ进行微分可得：

联立公式(6)和公式(8)，可得f1＝dx/dθ数学表达式：

公式(9)为一个微分方程，其中μ为折射非球面出射光线与光轴之间的夹角，作为一个未知参量，应当消去，从而公式(9)可求解出数值解；此时根据公式(4)可得：

y＝rmax·sinθ/sinθ1(10)

根据led与折射非球面的几何关系，可得μ、x、θ之间的数学关系，具体为：

联立公式(10)和公式(11)，可得到一个非线性方程f2＝0，具体为：

联立公式(9)和公式(12)，得到一组微分代数方程该方程组的数值解即为构成折射非球面离散点坐标。

(2)全内反射非球面结构示意图如图3所示，和步骤(1)类似，在确定由全内反射非球面调控均匀光斑半径r′max＝1000mm和折射非球面最大半径h＝4.609mm后，基于led与折射非球面的几何关系、光通量守恒公式和snell定律，推导得出一组daes，具体过程为：

基于led与全内反射非球面的几何关系和snell定律，可推导得出一个微分方程f3，其表示全内反射非球面各点横坐标x′和led出射角θ′、dx′/dθ′之间的数学关系，具体为：

公式(13)为一个微分方程，其中f3＝dx′/dθ′，再由光通量守恒可知，目标面所接收的期望光通量与led到达全内反射非球面的光通量相等，得到led与全内反射非球面的光通量守恒公式，根据照度均匀原则，led出射光经全内反射非球面调控后在目标面各采样点的辐照度应相等，将该原则代入光通量守恒公式，并根据led与全内反射非球面的几何关系，可得全内反射非球面各点纵坐标y′surface与全内反射非球面出射光线与光轴之间的夹角μ′、x′、θ′之间的数学关系f4，具体为：

联立公式(13)和公式(14)，得到一组微分代数方程该方程组的数值解即为构成全内反射非球面离散点坐标。

(3)在数学计算软件matlab2018b中编写解算程序，采用runge-kutta法，将其步长分别设置为θ1/100rad和0.05rad，求解范围分别为[0,θ1]和(θ1,θmax]，分别求解步骤(1)推导的和步骤(2)推导的的数值解，从而得到两组离散点的坐标，分别为折射非球面离散点坐标和全内反射非球面离散点坐标；

本发明所述方法求解的折射非球面在x0y平面内的离散点坐标分别为(-10.000,0.000,0.000)，(-10.000,0.039,0.000)，(-10.000,0.079,0.000)，…，(-10.391,4.467,0.000)，(-10.391,4.537,0.000)，(-10.391,4.609,0.000)；同时，本发明所述方法求解的全内反射非球面在x0y平面内的离散点坐标分别为(-15.000,6.047,0.000)，(-14.970,6.089,0.000)，(-14.943,6.135,0.000)，…，(-4.642,17.151,0.000)，(-4.522,17.233,0.000)，(-4.403,17.311,0.000)；利用最小二乘法将两组离散点坐标各自拟合成平滑的二维曲线，其中离散点的数量决定二维曲线的精度；将求解所得的二维曲线导入至制图软件solidworks2012，将二维曲线绕光轴旋转一周得出一个旋转对称形透镜。

(4)自由曲面的求解如图3所示，对于不同形状的定制光斑，首先确定光斑定制区域边界在笛卡尔坐标系中坐标(xd,yd)，再将其转换为极坐标(r,β)，其中r即光斑定制区域在不同方向的横截面上的边界位置，β∈[0,2π]表示方向，本发明以定制矩形光斑(宽为1000mm)为例，将其矩形边界各点的笛卡尔坐标转换为极坐标(rp,βp)，并以此为边界条件，再根据led与全内反射非球面的几何关系和snell定律，逆向推导得出自由曲面在任意方向的横截线段x″＝xp(自由曲面在任意方向的横截线段为垂直于x轴的直线)与对应led出射角θp之间的数学关系，具体为：

结合光通量守恒公式，可得θp与rp、θ1之间的数学关系，具体为：

此时，任意方向上的边界条件rp为已知条件，联立公式(15)和公式(16)，可求解得出xp的数值解，即自由曲面在任意方向横截线段，将其导入至solidworks2012制图软件，通过闭合放样得到一个自由曲面，其中横截线段数量越大，所得自由曲面的面型精度越高；以矩形定制光斑为例，所述方法求解的各方向xp分别为(-15.000,-14.033,-13.654,…,-11.430,…,-13.654,-14.033,-15.000)。

(5)如图1所示，将步骤(4)所得自由曲面与步骤3)所得的透镜导入至solidworks2012制图软件，通过布尔运算进行组合，最终构成本发明所设计的新型全内反射透镜。

(6)将步骤(5)所得新型全内反射透镜导入到非成像光学设计软件lighttools8.4.0中进行仿真验证，初始化led目标面，按照设计参数确定其位置，设置led光强分布为朗伯体，新型全内反射透镜折射率为1.643，其中透镜主体属性为“平滑光学”，“光线传播方向”属性设置为“透射/tir光线”，自由曲面属性为“朗伯散射”，光线追迹数量为1000000条，对模型进行monte-carlo光线追迹，本发明以矩形定制光斑以及2:1辐照度比为例，仿真结果如图4所示，其光斑定制区域的辐照均匀度达到95.3％，背景区域的辐照均匀度达到89.3％，led能量利用率为89.3％，且光斑定制区域的辐照度平均值(>1.6e-05w/m²)与背景区域辐照度平均值(>8e-06w/m²)比值接近2:1，与设计参数符合。

(7)为了验证本发明所述方法对光斑形状的定制性能，基于所述方法设计了曲形的定制光斑，辐照度比值为2:1，图5展示了透镜示意图(a)及其产生的辐照分布图(b)，其光斑定制区域的辐照均匀度达到95.6％，背景区域的辐照均匀度达到80.2％，led能量利用率为83.2％，且光斑定制区域的辐照度平均值(>1.6e-05w/m²)与背景区域辐照度平均值(>8e-06w/m²)比值接近2:1，与设计参数符合。

为了验证本发明所述方法对于辐照度层次的调控性能，基于所述方法设计了矩形形状的光斑定制区域，辐照度比值为5:1，图6展示了透镜示意图(a)及其产生的辐照分布图(b)，其光斑定制区域的辐照均匀度达到85.4％，背景区域的辐照均匀度达到84.8％，led能量利用率为82.4％，且光斑定制区域的辐照度平均值(～1.9e-05w/m²)与背景区域辐照度平均值(～3.8e-06w/m²)比值接近5:1，与设计参数符合。

本发明的上述实施例并不对本发明构成限制，参照本发明的描述，所公开的实施例的其他变化，都属于本发明权利要求限定的范围之内。