大视场向心辐照高能聚光器及设计方法

1.本发明涉及聚光器技术领域，特别是一种适合用于高功率激光领域的大视场向心辐照高能聚光器及其设计方法。


背景技术：

2.激光惯性约束聚变(icf)对于高能物理研究以及未来清洁能源的开发具有重要意义。在激光惯性约束聚变中，需要将具有高能量的激光脉冲聚焦于靶丸上，来实现对靶丸的压缩，使靶丸内部达到发生聚变反应所需要的高温高压的条件。在激光辐照靶丸的过程中，产生的等离子体冕区会与入射的激光发生相互作用，导致激光能量的耗散，进而使激光与靶丸之间的能量耦合效率降低。
3.前期的研究证明，相比于常规的平面靶和球形靶，锥型靶能够有效提高激光与靶丸之间的耦合效率。由于锥靶具有一定的立体角，因此只有位于锥靶立体角以内的光束可以进入锥靶，处于锥靶立体角以外的光束，则无法进入锥靶。由此可见，锥靶的结构限制了辐照光束的入射角度，使得最终作用于靶丸的光束数量受到限制，进而限制了注入靶丸的激光能量，导致icf激光装置的输出能力无法得到充分利用。为了在提高束靶耦合效率的同时，充分发挥激光装置的输出能力，将尽可能多的能量注入到靶丸中，寻找一种可以在不改变现有靶室激光排布以及不影响光束向心性和辐照均匀性的前提下，解决锥靶icf实验中激光入射角度受限问题的方案是十分必要的。


技术实现要素：

4.本发明的目的是提供一种大视场向心辐照高能聚光器的设计方法，以解决锥靶icf实验中，辐照光束入射角度受到锥靶立体角限制的问题。
5.本发明的技术方案是：
6.一种大视场向心辐照高能聚光器，其特征在于，
7.该装置具有两个同轴球状折射面(如图1(a)所示)，其中第一折射面1为凸球面，第二折射面2为凹球面，且两个球面同轴。光束在进入聚光器时，通过第一个面1的折射，使原本处于锥靶立体角以外的光束进入到锥靶立体角以内，并通过第二个面2的折射，使入射的光束最终能够满足锥靶对光束入射角度的要求，提高最终注入靶丸的激光能量；
8.进一步的，该装置在改变光束注入角度的同时，不改变光束的聚焦位置，使光束在经过调整后仍然保持原来向心的状态；
9.进一步的，考虑到icf实验中的高能量，本发明采用具有高损伤阈值的材料，如lbo晶体等。
10.本发明还提供一种聚光器件的设计方法，包含以下步骤：
11.(1)根据使用的实际情况，确定入射边缘光线和出射边缘光线与光轴的夹角，以及第一折射面1的曲率半径及其极点与焦点之间的距离；
12.(2)通过光线追迹方法对光线在聚光器内部和通过聚光器后的传输方向进行计
算，得到两个折射面极点在光轴上的间距与第二个折射面2曲率半径之间的关系；
13.(3)利用光线在第二折射面2折射前后角度的关系为约束条件，最终确定两个折射面极点在光轴上的间距与第二个折射面2曲率半径。
14.本发明的有益效果是：
15.1、通过对聚光器两个表面参数的设计，本发明可以在不改变聚焦位置的情况下，实现对光束聚焦角度的调整；
16.2、具有高损伤阈值材料(如lbo晶体)的使用，本发明可以承受较高激光功率，可以应用于高功率激光系统中；
17.3、在锥靶icf实验中，使原本处于锥靶空间立体角以外无法进入锥靶的光束可以进入锥靶，在不改变靶室布局的前提下，解决锥靶icf实验中激光入射角度受限的问题。
附图说明
18.图1为本发明大视场向心辐照高能聚光器结构示意图(a)以及三视图(b)；
19.图2为本发明中所用光线追迹方法的示意图；
20.图3锥靶icf实验中，由于锥靶结构导致辐照光束入射角度受限的示意图
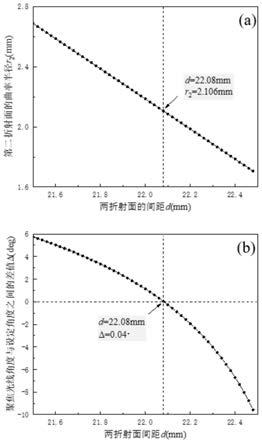
21.图4为数值计算求解第二个折射面2位置及曲率半径的结果；
22.图5为本发明的实施例效果图。
23.图中：1聚光器第一折射曲面；2聚光器第二折射曲面；3聚光器侧面；4锥靶；5锥靶允许的最大入射角度；6处于锥靶空间立体角以内的光束；7处于锥靶空间立体角以外无法进锥靶的光束；8经过所述聚光器第一折射面折射后的光束；9经过所述聚光器第二折射面折射后的光束，即出射光束。
具体实施方式
24.下面将结合说明书附图对所述的大视场向心辐照高能聚光器及其设计方法进行详细介绍。
25.在icf实验中，为了保证激光与靶丸之间的能量耦合效率，需要严格控制辐照在靶丸上的光场的均匀性。为了使激光辐照的均匀性不受影响，经过聚光器后进入锥靶的光束应尽可能满足以下两个条件：(1)光束的传输方向仍然是向心的，即光束的聚焦位置与原聚焦位置一致，以保证光束的辐照方向指向锥靶的顶点；(2)经过聚光器后，光束的空间分布应尽可能均匀，以保证激光辐照的均匀性。
26.在所述聚光器设计过程中，用光线来代替实际光束，并采用边缘子午光线追迹的方法计算所述聚光器的面型参数。所述光线追迹方法如图2所示，其中各参数的符号定义如下：假定光线从左侧入射，聚焦点位于所述聚光器的右侧。以折射面的极点为坐标原点，当光线与光轴的交点位于折射面右侧时，其与坐标原点之间的距离为正，反之为负；当曲率中心在折射面极点右侧时，曲率半径为正，反之为负；若以光线与光轴的交点为中心，光轴顺时针转动小于90度能与光线重合，则光线与光轴的夹角为正，反之为负；若入射(或折射)光线绕其与折射面的交点转动小于90度能与法线(即折射面曲率半径)重合，则入射角(或折射角)的角度为正，反之为负。
27.如图2(a)所示，空气与聚光器所用材料的折射率分别为n0和n1，入射光线与光轴的
夹角β1已知，根据实际需求设定最终出射光线与光轴的夹角β
′2，定义光束汇聚比m＝β1/β
′2。a1为第一折射面1的极点，光线在第一折射面1的折射过程中，以a1为坐标原点，p1为入射光线与第一折射面1的交点，b1为入射光线与光轴的交点，b1′
为经过第一折射面1折射后的光线与光轴的交点，定义a1b1所对应的长度为l1，即第一折射面1的极点与聚焦点之间的距离，a1b
′1所对应的长度为l
′1，c1为第一折射面1的曲率中心，则p1c1即为第一折射面1上p1处的法线，长度为r1，入射角与折射角分别为α1与α
′1，折射光线与光轴的夹角为β
′1，对于第一折射面1上发生的折射过程，可以发现，在δp1c1b1中，利用正弦定理可以得到
[0028][0029]
利用折射定律可以得到入射角α1与折射角α
′1满足
[0030]n0 sinα1＝n
1 sinα
′1ꢀꢀ
(2)
[0031]
利用三角形角度关系可以得到
[0032]
β
′1＝β1+α
1-α
′1ꢀꢀ
(3)
[0033]
在δp1b
′1c1中，通过正弦关系得到
[0034][0035]
光线通过第一个折射面1的折射到达第二个折射面2，并在第二个折射面2发生第二次折射。如图2(b)所示，以第二个折射面的极点a2为坐标原点，光轴上两个折射面极点之间的间距为d，c2为第二个折射面2的曲率中心，r2为其曲率半径，以a2为坐标原点，经过第一个折射面1折射的光线与第二个折射面2交于p2，与光轴交于b
′1，夹角为β2，定义a2b
′1长度为l2，出射光线与光轴的交点仍然位于b1，与光轴的夹角为β
′2，定义c2b1的长度为l
′2，入射光线和折射光线与法线p2c2的夹角分别为α2与α
′2。再次利用光线与法线以及光轴构成的三角形的关系，对于光线在第二个折射面上的折射过程，可以得到如下关系：
[0036][0037]n1 sinα2＝n
0 sinα
′2ꢀꢀ
(6)
[0038]
β2＝β
′2+α
′
2-α2ꢀꢀ
(7)
[0039][0040]
利用传递方程，得到两个面的参数之间有如下关系：
[0041]
β
′1＝β2ꢀꢀ
(9)
[0042]
l2＝l
′
1-d
ꢀꢀ
(10)
[0043]
由于经过聚光器的光束聚焦位置与原光束相比不发生变化，因此，
[0044]
l1＝l
′2+d
ꢀꢀ
(11)
[0045]
利用(1)-(6)和(8)-(11)可以得到
[0046][0047]
由于d是未知的，因此无法利用(7)式直接求出r2与r1的关系，但利用数值求解的方
法，通过求解(7)式和(12)式构成的方程组可以得到设定l1和r1后r2和d的值。
[0048]
下面通过一个设计实例，对本发明所述大视场向心辐照高能聚光器的设计过程进行说明。
[0049]
icf实验中，采用多束激光从不同方向同时辐照靶丸，如图3所示，锥靶4的结构限制了光束的入射方向，锥靶所对应的空间立体角决定了其所允许的光束的最大入射角度5，处于锥靶空间立体角以内的光束6满足入射条件，可以不受靶壁的影响，直接入射到靶丸内部，但是入射角度大于锥靶所允许的最大入射角度5的光束7，则无法进入锥靶。本发明大视场向心辐照高能聚光器可以实现对光束角度的调整，从而解决这一问题。
[0050]
设计所述大视场向心辐照高能聚光器的材料以具有高损伤阈值的lbo晶体(在350nm波段，脉冲持续时间7ns的情况下，可以承受大于0.14gw/cm2的激光功率密度)为例(但不限于lbo晶体)，其在激光波长为351nm时对应最大折射率为nz＝1.6439，因此在实际应用过程中，应调整光束偏振方向，使光束对应最大折射率。
[0051]
设计过程中，以子午面上的边缘光线作为光线追迹的对象，对确定第一折射面1参数情况下的第二折射面2参数进行数值计算。设定参数l1＝30mm，第一折射面1的曲率半径r1＝21mm，入射光线与光轴的夹角β1＝30
°
，出射光线与光轴的夹角β
′2＝15
°
。通过上述方法计算得到，满足(12)式的r2和d的关系如图4(a)中的实线所示，通过数值求解，得到在d取不同值的情况下，最终出射光线与光轴的夹角与设定角度的差值变化曲线如图4(b)所示，选曲线中差值为零的点对应的横坐标即为满足(7)式和(12)式所给出条件的d的取值，对应于图4(a)中曲线的纵坐标即为r2的取值。通过数值求解，得到在给定条件下，d＝22.08mm，r2＝2.106mm。
[0052]
下面给出本发明的一个设计实例。
[0053]
以上述过程中计算得到的参数为依据，设计聚光器，并对入射角度为
±
10
°
、
±
20
°
和
±
30
°
的光线进行光线追迹，光线入射角度与锥靶允许的最大入射角度如图4所示。图5给出了所述不同入射角度的光线在通过大视场向心辐照聚光器后的光线追迹的结果，可以看出，原本处于锥靶立体角以外，无法注入锥靶的光束7，经过所述大视场向心辐照聚光器的调整后，可以注入到锥靶内部，同时入射到锥靶之后的光线具有较好的向心性以及空间分布的均匀性，这使得锥靶icf实验中光束辐照角度受限的问题得到了解决。