一种基于蜂窝光子晶体的拓扑光子晶体光波导结构

1.本发明涉及光子晶体的技术领域，尤其是涉及一种基于蜂窝光子晶体的拓扑光子晶体光波导结构。


背景技术：

2.近几十年来，拓扑绝缘体作为凝聚态物理的一个重要领域，成为当前的研究热点之一,光学拓扑绝缘体是对电子拓扑绝缘体的模拟,该材料内部为绝缘体，边缘存在受拓扑保护的边界态，电磁波可以沿着边缘进行单向传输，背向散射被抑制，并且免疫无序，杂质等缺陷。拓扑光子晶体在很多领域得到应用，如：拓扑激光器、鲁棒的光学延时线、光波导器件等。实现光学系统中的量子自旋霍尔效应的关键在于实现kramers简并，目前的主要方法是利用六个介质柱构建具有c6对称的蜂窝晶胞，在蜂窝晶胞的带隙内实现了四重偶然简并的狄拉克点。通过对蜂窝晶胞进行压缩和拉伸可以打开光子带隙，实现能带反转，拓扑相变。这种方法在实际应用中较为繁琐，并且在调控时相对困难。


技术实现要素：

3.本发明针对现有技术的不足，提出了一种基于蜂窝光子晶体的拓扑光子晶体光波导结构，仅需要改变介质柱的介电常数，就可以实现双重狄拉克锥，在不改变晶格常数、介质棒的大小和位置等其他因素的情况下，控制内圈与外圈的介质柱的介电常数就可以实现拓扑平庸到拓扑非平庸的转变，解决了背景技术中提到的问题，传输效率高，光子局域性能强且自由度高，相比于传统方法中对蜂窝晶格采取压缩或拉伸的方法，本发明采取的方案更加简单灵活，更易在实际中进行应用。同时基于上述提出的拓扑平庸和拓扑非平庸的拓扑光子晶体，设计了一种新型分束器结构，在分束器工作带宽内的电磁波可以在沿着拓扑平庸和非平庸界面鲁棒的进行单向传输。
4.为实现上述目的，本发明提供了一种基于蜂窝光子晶体的拓扑光子晶体光波导结构，包括光子晶体波导结构，所述光子晶体波导结构由两个部分组成，上半部分是由具有拓扑平庸性质的晶胞在空气中排列组成，下半部分是由具有拓扑非平庸性质的晶胞在空气中排列而成；
5.拓扑平庸性质的晶胞与拓扑非平庸性质的晶胞均由12个横截面为圆形的介质柱组成，6个介质柱为一组，按照c6的结构组成了一大一小的两个正六边形，再将内圈介质柱旋转一定的角度，与外圈介质柱组合形成正六角星形结构；
6.从晶胞中心到内侧介质柱的距离为r1，内侧介质柱的介电常数为ε1，内侧介质柱的半径是r1；从晶胞中心到外侧介质柱的距离为r2，外侧介质柱的半径是r2，处于外侧介质柱的介电常数为ε2；外侧介质柱与内侧介质柱的距离差距为s＝r
2-r1，相邻晶胞中心之间的距离是晶格常数a0，空气的介电常数ε0是1。
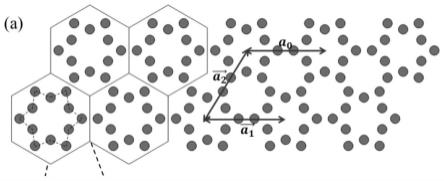
7.优选的，每一个晶胞在空气中均按照三角点阵排列而成，点阵向量和
其中晶格常数a0＝346μm，和是三角形晶格基本向量，a为水平向量的长度。
8.优选的，圆形介质柱的半径r为0.04a0到0.06a0，介质柱的高度为0.6a0。
9.优选的，当1≤ε≤12，分为以下情况：
10.当ε1＝ε2＝12时拓扑光子晶胞具有双重狄拉克锥，表现为蜂窝晶胞；
11.当ε1《ε2＝12时拓扑光子晶胞具有拓扑平庸性质；
12.当ε2《ε1＝12时拓扑光子晶胞具有拓扑非平庸性质。
13.优选的，拓扑平庸性质的晶胞和拓扑非平庸性质的晶胞均为4层结构。
14.优选的，当为拓扑平庸性质的晶胞时ε1＝5，ε2＝12；当为拓扑非平庸性质的晶胞时，ε1＝12，ε2＝5。
15.优选的，将上述光子晶体波导结构应用在分束器中，所述分束器在0.555-0.575(2πc/a)的工作频率范围内的波动在[0,1.5]之间。
[0016]
本发明提出的一种单胞光子晶体具体为：在蜂窝晶格中用十二个介质柱替换原来6个介质柱，且使这十二个介质柱的中心相互连接呈正六角星。该晶胞单元结构可以通过三种方式实现拓扑相变：
[0017]
(1)当十二个介质柱的大小固定时，可以压缩或拉伸介质柱；
[0018]
(2)当a0/r＝3时，改变内圈或外圈介质柱的大小；
[0019]
(3)当介质柱的大小和a/r为定值时，改变内圈或外圈介质柱的介电常数。通过计算不同结构参数复杂单胞的能带图，三种方式均实现了拓扑相变的机制，设计并模拟仿真实现了光流的向右单向传输，该波导有望在光子集成器件中得到应用。
[0020]
本发明提出了一种新型的晶胞结构，与前人所提出的结构相比有更大的自由度，能够自由转动或者改变其大小，可调的参数与六个介质柱的单胞相比更多，并且能在一种结构内实现三种拓扑相变；还提出了一种实现拓扑相变的新机制：在不改变介质棒大小及位置的情况下，通过改变外圈与内圈介质棒的介电常数，就能实现拓扑相变。
[0021]
因此，本发明采用上述一种基于蜂窝光子晶体的拓扑光子晶体光波导结构，采用十二根介质柱，通过改变内外圈介质柱的介电常数来控制拓扑相变，并能在一种结构内通过不同的方法来实现三种拓扑相变，使用更加灵活方便。
[0022]
下面通过实施例，对本发明的技术方案做进一步的详细描述。
附图说明
[0023]
图1为本发明中晶胞在空气中排列的结构图；
[0024]
图2为本发明单晶胞内部结构；
[0025]
图3为本发明中将三角形晶格的第一个bz重构为菱形；
[0026]
图4为本发明中为当a0/r＝3时，r1＝r2＝0.06a0时，δε＝ε
1-ε2时，蜂窝晶格单胞中ω
pd
和|δω|随δε的变化趋势；
[0027]
图5为本发明中当a0/r＝3，ε1＝ε2＝12时，蜂窝晶格单胞中ω
pd
和|δω|随r2/r1的变化趋势；
[0028]
图6为本发明中是当r1＝r2＝0.06a0，ε1＝ε2时，蜂窝晶格单胞中狄拉克点频率随ε
的变化趋势；
[0029]
图7为本发明中是当r1＝r2分别为0.06a0、0.05a0和0.04a0时，蜂窝晶格单胞中a0/r随s的变化趋势；
[0030]
图8为本发明中a0/r＝3，r1＝r2＝0.06a0时，外圈与内圈介质棒介电常数分别为ε1＝5，ε2＝12(a),ε1＝ε2＝12(b)和ε1＝12，ε2＝5(c)的能带结构图；
[0031]
图9为本发明中记录的拓扑相变的过程；
[0032]
图10为本发明中拓扑平庸与拓扑非平庸构建的超胞及超胞对应的带状色散曲线图；
[0033]
图11为本发明中是基于图10的新型超胞及超胞对应的带状色散曲线图；
[0034]
图12为本发明中所设计的光子晶体波导在0.555(2πc/a)时的电场图，上半部分是拓扑平庸结构，下半部分是拓扑非平庸结构；
[0035]
图13为本发明中所设计的光子晶体波导在0.565(2πc/a)时的电场图；
[0036]
图14为本发明中所设计的光子晶体波导在0.555-0.595(2πc/a)范围内的传输效率图；
[0037]
图15为本发明中所提出的分束器结构示意图；
[0038]
图16为本发明中电磁波在该结构中的传输模场图；
[0039]
图17为本发明中的分束器在0.555-0.575(2πc/a)范围内两输出端口的能量统计；
[0040]
图18为本发明中是p
out2
/p
out1
的分流比曲线，在此工作频率范围内波动在[0,1.5]之间；
[0041]
图19为本发明中该分束器结构中构建了空腔和无序两种不同缺陷的结构示意图；
[0042]
图20为本发明中分束器在具有两种不同缺陷的结构所对应的坡印廷矢量。
具体实施方式
[0043]
本发明提供了一种基于蜂窝光子晶体的拓扑光子晶体光波导结构，包括光子晶体波导结构，所述光子晶体波导结构由两个部分组成，上半部分是由具有拓扑平庸性质的晶胞在空气中排列组成，下半部分是由具有拓扑非平庸性质的晶胞在空气中排列而成；拓扑平庸性质的晶胞和拓扑非平庸性质的晶胞均为4层结构。
[0044]
拓扑平庸性质的晶胞与拓扑非平庸性质的晶胞均由12个横截面为圆形的介质柱组成，6个介质柱为一组，按照c6的结构组成了一大一小的两个正六边形，再将内圈介质柱旋转一定的角度，与外圈介质柱组合形成正六角星形结构；从晶胞中心到内侧介质柱的距离为r1，内侧介质柱的介电常数为ε1，内侧介质柱的半径是r1；从晶胞中心到外侧介质柱的距离为r2，外侧介质柱的半径是r2，处于外侧介质柱的介电常数为ε2；外侧介质柱与内侧介质柱的距离差距为s＝r
2-r1，相邻晶胞中心之间的距离是晶格常数a0，空气的介电常数ε0是1。
[0045]
每一个晶胞在空气中均按照三角点阵排列而成，点阵向量和其中晶格常数a0＝346μm，和是三角形晶格基本向量，a为向量在水平方向的长度。
[0046]
圆形介质柱的半径r为0.04a0到0.06a0，介质柱的高度为0.6a0。
[0047]
当1≤ε≤12，分为以下情况：
[0048]
当ε1＝ε2＝12时拓扑光子晶胞具有双重狄拉克锥，表现为蜂窝晶胞；
[0049]
当ε1《ε2＝12时拓扑光子晶胞具有拓扑平庸性质；
[0050]
当ε2《ε1＝12时拓扑光子晶胞具有拓扑非平庸性质。
[0051]
本发明提出的一种单胞光子晶体具体为：在蜂窝晶格中用十二个介质柱替换原来6个介质柱，且使这十二个介质柱的中心相互连接呈正六角星，该晶胞单元结构可以通过三种方式实现拓扑相变：
[0052]
(1)当十二个介质柱的大小固定时，可以压缩或拉伸介质柱；
[0053]
(2)当a0/r＝3时，改变内圈或外圈介质柱的大小；
[0054]
(3)当介质柱的大小和a0/r为定值时，通过计算不同结构参数的复杂单胞能带图，改变内圈或外圈介质柱的介电常数。以上三种方式均实现了拓扑相变的机制，设计了波导结构并模拟仿真实现了光流的向右单向传输，该波导结构可以在光子集成器件中得到应用。
[0055]
将上述光子晶体波导结构应用在一种1x2的分束器中，所述分束器在0.555-0.575(2πc/a)的工作频率范围内的波动在[0,1.5]之间。
[0056]
本发明提出了一种新型的晶胞结构，与前人所提出的结构相比有更大的自由度，能够自由转动或者改变其大小，可调的参数与六个介质柱的单胞相比更多，并且能在一种结构内实现三种拓扑相变；还提出了一种实现拓扑相变的新机制：在不改变介质棒大小及位置的情况下，通过改变外圈与内圈介质棒的介电常数，就能实现拓扑相变。
[0057]
以下通过实施例对本发明的技术方案作进一步说明。
[0058]
实施例
[0059]
本发明所设计的拓扑光子晶体结构，晶胞的二维截面是由12个圆形介质柱呈c6对称排列。所述的背景材料是空气，介质柱的高度为0.6a0晶胞的截面是正六边形，两个相邻晶胞中心的距离是晶格常数a0＝346μm。六边形晶胞的中心到棒1的距离为r1，到棒2的距离为r2，记s＝r
2-r1。距离六边形晶胞中心较近的内圈介质柱和较远的外圈介质柱半径分别是r1和r2，这提出了一种新型的晶胞结构，该结构与传统结构相比有更大的自由度，即能够自由移动或转动或改变其大小，可调的参数与六个介质柱的单胞相比更多，并且能在一种结构内实现三种拓扑相变。
[0060]
本发明中实现光量子自旋霍尔效应的关键是实现kramers简并。拓扑相变时带隙会经历打开-合并-打开的过程。双重狄拉克锥就是拓扑相变点，当双重狄拉克锥的分离会打开一个光子带隙，如果上方能带d轨道的频率大于下方能带p轨道的频率，则该结构表现为拓扑平庸结构；如果上方能带p轨道大于下方能带d轨道的频率，则该结构表现为拓扑非平庸结构；
[0061]
因此，本发明通过改变介质柱的介电常数就可以影响能带轨道频率，当ε1＝5，ε2＝12时，e
p
＜ed，结构表现为拓扑平庸结构；当ε1＝ε2＝12时，e
p
＝ed，结构表现为蜂窝结构；如当ε1＝12，ε2＝5时，e
p
＞ed，结构表现为拓扑非平庸性质；本发明的上半部分为拓扑平庸结构(ε1＝5，ε2＝12)，下半部分是拓扑非平庸结构(ε1＝12，ε2＝5)，在两种不同拓扑性质的界面处会出现受拓扑保护的螺旋边界态，图10中显示了超胞的结构及其色散曲线图，从图中可以发现在光子带隙中出现了一对边界态。该波导结构的工作带宽在0.555-0.595(2πc/
a)，其中c为光速。图11中构造了一种新型超胞结构并制出色散曲线图，图11中显示了pc4的介电常数在8.2-8.8变化时，边界态的从上到下的移动情况，从图可以看出，当pc4的介电常数降低时，下边界态发生红移。
[0062]
将图12是对应的图10的光子晶体波导在0.555(2πc/a)时的电场图，光波导的上半部分是拓扑平庸结构，下半部分是拓扑非平庸结构；图13是对应于图11所设计的光子晶体波导在0.565(2πc/a)时的电场图；图14是图12与图13在0.555-0.595(2πc/a)范围内的传输效率图。从图中可以发现电磁波沿着平庸和非平庸截面稳定的单向传输，背向散射被抑制，并且光流主要局域在界面的非平庸层。这是因为传播方向被伪自旋的极化锁定，每条路径只允许具有特定伪自旋方向的电磁波单向传播。图13这种新型波导的传输方式大大降低了传输损耗，并且传输率与传统波导相比有所提高。
[0063]
图15是对应图13所设计的拓扑光子晶体分束器结构，对当前结构进行模拟仿真，绘制出在0.5633thz频率下的电场分布，如图16所示，为了得到更加准确的评估该分束器的性能，模拟了在0.555-0.575thz工作频率范围内情况，在每个输出通道中通过在两个输出端口的位置插入探针来检测透射光谱，计算了工作频率下每个输出通道中电磁波的归一化功率值，得到电磁波的归一化功率值图17；通过输出端口的能量，可以得到系统分光比曲线图18，在图17中可以观察到，在0.5633thz和0.5685thz的频率下功率值相等，这意味着在这两个频率下实现了等功率分束。通过分流比曲线图，它在0.555-0.575(2πc/a)的工作频率范围内波动在[0,1.5]以内，所以可以在这个波动范围内调节两个输出波的能量比。
[0064]
为了验证分束器结构的鲁棒性，在结构中制造缺陷，通过删除两个相邻的散射体构造缺陷腔，还通过互换两个相邻的拓扑光子晶体晶胞的位置引进无序，然后对当前结构进行模拟仿真，并且绘制了它的模场分布图，如图19所示，从图中可以发现电磁波能够沿着界面鲁棒的传输，对空腔和无序这两种缺陷免疫，并且没有明显的背向散射和能量损耗。图20显示了图19所对应平面内时间平均面内坡印廷矢量的分布，结果表明，电磁波沿界面的传播是涡旋状的，这与qshe的固有特征相一致。
[0065]
以下通过附图来对本发明的技术方案作进一步说明。
[0066]
在图1至图3中，本发明提出一种新结构，通过将十二根介质柱分成内外两组，并将内圈的介质柱旋转一定的角度，形成了一种新的六角形结构，在图1中，晶格常数a0＝346μm，单胞在空气中按三角点阵排列，和是三角形晶格中的基本向量，点阵向量和通过有限元仿真软件求解本征方程，从而得到光子晶体的本征态和能带结构，沿着晶胞第一布里渊区k
→
γ
→
m进行扫描，其中k1和k2为倒易晶格的基元向量，因此可以通过电子束蚀刻，干法蚀刻或者双光子聚合来制备当前的拓扑光子晶体结构。
[0067]
在图4至图7中，则是总结了其他因素对本技术的影响，在图4中，当介质棒的位置和大小固定时，蜂窝晶格单胞中ω
pd
和|δω|随介电常数差值的变化趋势图；在图5中，记录的是当介质柱的位置和介电常数固定时，蜂窝晶格单胞中ω
pd
和|δω|随外圈介质柱半径与内圈介质柱半径的比值的变化趋势；在图6中，当介质柱的半径都为0.06a0时，且介质柱的介电常数都保持一致，记录蜂窝晶格单胞中狄拉克点频率随介电常数的变化趋势；在图7中，让所有介质柱的半径都相等，当介质柱半径分别取为0.06a0、0.05a0和0.04a0时，蜂窝晶
格单胞中a0/r随s的变化趋势；
[0068]
通过这些测试，可以记录其他因素对晶胞的影响效果，说明本技术在不使用改变内圈与外圈介质棒的介电常数的情况下，依然可以使用传统方法来进行调控，方便使用。
[0069]
在图8至图9中，则是本技术在a0/r＝3，r1＝r2＝0.06a0的情况下，通过改变内圈介质柱和外圈介质柱的介电常数，来记录介电常数对光子晶体的影响，图8中分别给出了ε1＝5，ε2＝12,ε1＝ε2＝12和ε1＝12，ε2＝5三种不同组合的介电常数，当ε1＝5，ε2＝12时，其具有拓扑平庸性质；当ε1＝ε2＝12时，其具有双重狄拉克锥；当ε1＝12，ε2＝5时，其具有拓扑非平庸性质，灰色矩形区域是它们的公共带宽，根据介电常数的不同，表现出了不同性质，图9中，记录的是图8中拓扑平庸性质到拓扑非平庸性质的拓扑相变的过程。
[0070]
图10记录的是拓扑平庸与拓扑非平庸构建的超胞及超胞对应的带状色散曲线图，带隙中出现了一对受拓扑保护的边界态，曲线斜率的正负分别表示自旋向上(点a)和自旋向下(点b)。
[0071]
图11则是基于图10中的新型超胞及超胞对应的带状色散曲线图，在超胞中引入缺陷并对边界添加扰动，下边界态会随着pc4介电常数的增加而逐渐红移。
[0072]
图12至图13记录的是在图10和图11的基础上设计的光子晶体波导的电场图，上半部分是拓扑平庸结构，下半部分为拓扑非平庸结构，图12是所设计的光子晶体波导在0.555(2πc/a)时的电场图；图13是所设计的光子晶体波导在0.565(2πc/a)时的电场图；
[0073]
图14记录的是基于图12和图13在0.555-0.595(2πc/a)范围内的传输效率图。
[0074]
图15到图20，是基于图13提出的分束器进行的测算，计算分束器的性能；图15中，是基于图13提出的分束器结构示意图，记录了分束器的结构排列；图16则是记录电磁波在该结构中的传输模场图，可以发现电磁波可以良好的从两输出端口输出，并能保持较好的单向性；在图17中记录的则是在0.555-0.575(2πc/a)范围内两个输出端口的能量，通过测算的能量，得出图18，p
out2
/p
out1
两输出端口能量的分流比曲线，从而算出在此工作频率范围内波动在[0,1.5]之间；
[0075]
在图19中，是在分束器结构中构建了空腔和无序两种不同缺陷的结构示意图，图20则是在分束器具有空腔和无序缺陷的情况下，分束器内的坡印廷矢量，根据矢量结果，能发现电磁波可以完美穿过空腔以及无序，并保持较好的单向性。
[0076]
因此，本发明采用上述一种基于蜂窝光子晶体的拓扑光子晶体光波导结构，通过改变晶胞内的介质柱的介电常数，将扰动引入到边缘状态，并分析了介电常数对边缘状态的影响。基于此，我们设计了一种新型拓扑分束器，该拓扑分束器具有较强的工作稳定性和抗干扰性，数值结果表明，该系统获得的分光比在0-1.5范围内，最大透过率可达98.8％。由于螺旋边缘态的拓扑性质，电磁波可以平稳地流过结构的各个角落而没有明显的能量损失。具有高自由度的蜂窝光子晶格pc能够实现丰富的能带结构，其散射体为棒状体，制造工艺简单，有良好的应用前景。
[0077]
最后应说明的是：以上实施例仅用以说明本发明的技术方案而非对其进行限制，尽管参照较佳实施例对本发明进行了详细的说明，本领域的普通技术人员应当理解：其依然可以对本发明的技术方案进行修改或者等同替换，而这些修改或者等同替换亦不能使修改后的技术方案脱离本发明技术方案的精神和范围。