一种基于欠定卷积混叠模型的稀疏盲分离方法与流程

本发明涉及信号处理
技术领域：
，更具体地，涉及一种基于欠定卷积混叠模型的稀疏盲分离方法。
背景技术：
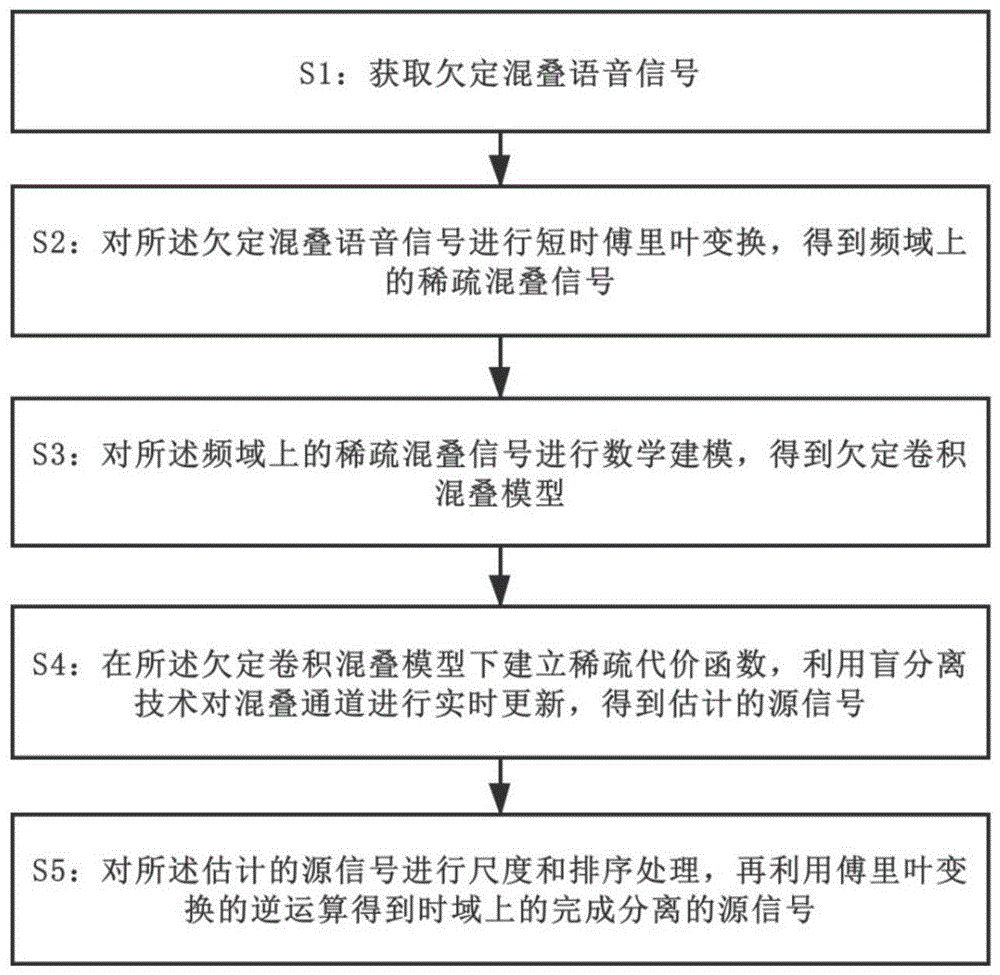
：盲源分离(blindsourceseparation,bss)是在混叠信道未知的情况下，仅仅从观测到的混叠信号中分离源信号。特别的，欠定的盲源分离问题引起了越来越多的关注，如何在源信号数目大于传感器的数目下的混叠信号中有效地分离源信号是一个极具挑战性的问题。目前，在解决卷积混叠盲分离问题上，主要采用独立元分析方法在假设源信号之间是相互独立的条件下，进行源信号的盲分离。然而，独立元分析在处理欠定的卷积混叠盲分离问题上有一定的局限性，因为独立元分析只能处理过定的或者正定的情形，即源信号数目小于或等于传感器的数目。为了解决欠定的情况，一般结合稀疏元分析理论对源信号进行盲分离，其中，稀疏元分析理论是假设源信号满足一定的稀疏性，即假设在每个频点上只有唯一的源信号是活跃的，其他的等于零或者接近于零。然而，时域上的信号并不具有很好的稀疏性。为了满足稀疏性的假设，常规的方法是利用短时傅里叶变换，把时域信号转换到频域上进行处理。但是，在源信号恢复阶段容易导致排序歧义性问题和尺度不确定问题，从而对盲分离结果带来了严重的影响。另外，由于混响时间过长还会导致混叠过程更加复杂，已有的多数卷积盲分离算法只能解决低混响的混叠信号，但无法解决高混响的混叠情形。技术实现要素：本发明为克服上述现有技术所述的欠定卷积混叠信号盲分离结果不理想的缺陷，提供一种基于欠定卷积混叠模型的稀疏盲分离方法。为解决上述技术问题，本发明的技术方案如下：一种基于欠定卷积混叠模型的稀疏盲分离方法，包括以下步骤：s1：获取欠定混叠语音信号；s2：对所述欠定混叠语音信号进行短时傅里叶变换，得到频域上的稀疏混叠信号；s3：对所述频域上的稀疏混叠信号进行数学建模，得到欠定卷积混叠模型；s4：在所述欠定卷积混叠模型下建立稀疏代价函数，利用盲分离技术对混叠通道进行实时更新，得到估计的源信号；s5：对所述估计的源信号进行尺度和排序处理，再利用傅里叶变换的逆运算得到时域上的完成分离的源信号。本技术方案用用于在欠定卷积混叠模型下对混叠信号进行分离，对所述待分离的混叠信号进行短时傅里叶变换，将混叠信号变换到频域上，并进行数学建模，得到欠定卷积混叠模型；然后，在此模型下构建稀疏代价函数，利用稀疏盲分离技术分离源信号；再对分离的源信号进行尺度和排序处理，使得估计的源信号与真实的源信号排序上保持一致。最后，利用傅里叶变换的逆运算将频域上估计的源信号变换到时域上，得到分离后的源信号。优选地，s1步骤中，采用在高混响的环境下，同时播放n组语音源信号，利用m个麦克风进行接收，获取欠定混叠语音信号，其中，n、m为正整数，且n>m。优选地，s3步骤中，所述欠定卷积混叠模型的表达公式如下：其中，n为源信号个数，l为卷积核的长度；hn＝[h1n,h2n,...,hmn]t表示第n个源信号在时频域上的脉冲响应；对于每个频点，利用矩阵的表示形式如下：xf＝hf*sf+nf其中，*表示卷积过程，表示卷积混叠系统，sf表示源信号，nf表示近似误差。优选地，s4步骤中，所述稀疏代价函数的公式如下：其中，||·||f表示frobenius范数；p是常数，且0<p≤1；λ为可调节的参数。优选地，s4步骤中，利用临近算子得到估计的源信号其计算公式如下：其中，(si)+＝max(0,si)。优选地，s5步骤中，对所述估计的源信号采用混叠阵矩阵进行列的标准化进行尺度处理，对所述估计的源信号采用方向到达角技术进行排序处理。为了避免尺度不确定性问题，本优选方案对混叠矩阵进行列的标准化；同时利用方向到达角技术弥补排序不一致问题，再利用傅里叶变换的逆运算，把频域上估计的源信号变换到时域上，从而得到分离的源信号。与现有技术相比，本发明技术方案的有益效果是：通过构建欠定卷积混叠模型，实现更好地、更精确地描述高混响环境下的混叠信号；通过构造稀疏代价函数，利用原信号的稀疏性更好地重构源信号；利用源信号的稀疏约束以及欠定卷积混叠模型的构造，在处理真实环境下的高混响混叠信号具有更明显的优势。附图说明图1为实施例1的基于欠定卷积混叠模型的稀疏盲分离方法的流程图。图2为实施例1的原始语音源信号的波形图。图3为实施例1的混叠通道的波形图。图4为实施例1的完成分离的源信号波形图。具体实施方式附图仅用于示例性说明，不能理解为对本专利的限制；对于本领域技术人员来说，附图中某些公知结构及其说明可能省略是可以理解的。下面结合附图和实施例对本发明的技术方案做进一步的说明。实施例1本实施例提出一种基于欠定卷积混叠模型的稀疏盲分离方法，如图1所示，为本实施例的基于欠定卷积混叠模型的稀疏盲分离方法的流程图。本实施例中的基于欠定卷积混叠模型的稀疏盲分离方法包括以下步骤：s1：获取欠定混叠语音信号。本实施例中，通过在网上公共语音数据集获取n组语音源信号，然后采用在高混响的环境下，同时播放上述获取的n组语音源信号，利用m个麦克风进行接收，获取欠定混叠语音信号，其中，n、m为正整数，且n>m。s2：对所述欠定混叠语音信号进行短时傅里叶变换，得到频域上的稀疏混叠信号。本实施例中，根据上述获得的稀疏混叠信号，为了保障源信号的稀疏性，通过计算机编程，在计算机上对所获得的欠定混叠语音信号进行短时傅里叶变换，把时域上的欠定混叠语音信号变换到频域上，得到更加稀疏的信号。s3：对所述频域上的稀疏混叠信号进行数学建模，得到欠定卷积混叠模型。本步骤中，欠定卷积混叠模型的表达公式如下：其中，n为源信号个数，l为卷积核的长度；hn＝[h1n,h2n,...,hmn]t表示第n个源信号在时频域上的脉冲响应；对于每个频点，利用矩阵的表示形式如下：xf＝hf*sf+nf其中，*表示卷积过程，表示卷积混叠系统，sf表示源信号，nf表示近似误差。s4：在所述欠定卷积混叠模型下建立稀疏代价函数，利用盲分离技术对混叠通道进行实时更新，得到估计的源信号。本步骤中，首先建立稀疏代价函数，其中，稀疏代价函数的公式如下：公式中，||·||f表示frobenius范数；p是常数，且0<p≤1；λ为可调节的参数；然后，利用临近算子计算得到估计的源信号其计算公式如下：其中，(si)+＝max(0,si)。s5：对所述估计的源信号进行尺度和排序处理，再利用傅里叶变换的逆运算得到时域上的完成分离的源信号。本步骤中，为了避免尺度不确定性问题，本实施例对混叠矩阵进行列的标准化；同时利用方向到达角技术弥补排序不一致的问题，再利用傅里叶变换的逆运算，把频域上估计的源信号变换到时域上，从而得到分离的源信号。进一步的，本实施例采用两组实验数据说明本实施例提出的基于欠定卷积混叠模型的稀疏盲分离方法的可行性和优越性。本实施例提出的实验数据是在windows10，inter(r)xeon(r)cpue5-2630v3@2.40ghz,32.00gb，matlabr2019a环境下实现的。首先，我们测试一组三个源信号两通道的欠定卷积混叠信号，数据集来自于“sisec2013”(http://sisec.wiki.irisa.fr/tiki-index.html)，选用真实记录的混叠信号：“dev1/dev1_female3_liverec_130ms_5cm_mix”，该混叠信号是由三个语音源信号两通道混叠而成。在欠定混叠语音信号获取过程中，所采用的两个麦克风之间的距离是5cm，混响时间为130ms。为了更好的说明本发明的可行性，我们测试不同参数p值对分离结果的影响，评价标准选用公用的sdr，sir，isr，sar的平均值作为参考。实验结果如下表1所示：表1三个语音源信号两通道的卷积混叠信号盲分离结果(db)0.10.20.30.40.50.60.70.80.91sdr1.283.182.522.821.961.441.974.194.904.18sir1.022.962.042.650.770.111.385.527.746.39isr4.125.975.726.135.174.905.617.728.567.89sar7.519.8410.538.4810.246.808.238.7910.857.51由表1结果可知，不同的p值产生的分离结果不同，在p＝0.9时盲分离结果最理想。同时，我们对比了本实施例提出的基于欠定卷积混叠模型的稀疏盲分离方法在p＝0.9时的原始信号与分离信号的波形图。如图2所示，为本实施例所采用的原始语音源信号的波形图，图3为混叠通道的波形图，图4为分离的源信号波形图。由图可知，通过对比图2和图4，可以发现本实施例待分离的混叠信号显然能够实现分离，因此本实施例所提出的基于欠定卷积混叠模型的稀疏盲分离方法具有可行性。本实施例还测试了一组由四个源信号三通道的欠定卷积混叠信号，数据集来自于“sisec2013”(http://sisec.wiki.irisa.fr/tiki-index.html)，选用真实记录的混叠信号：“dev3/dev3_female3_liverec_380ms_5cm_mix”。所选用的混叠信号是由四个语音源信号三通道混叠而成，在获取欠定混叠语音信号的过程中，所采用的是两个麦克风之间的距离是5cm，混响时间为380ms的高混响环境。本实施例对比了以下现有算法：full-rank算法、n-regu算法、c-palm算法，采用sdr值、sir值对实验结果进行判断。本实施例的实验结果如下表2所示：表2四个语音源信号三通道的卷积混叠信号盲分离结果(db)由表2结果可知，相比于其他现有的盲分离算法，本实施例提出的基于欠定卷积混叠模型的稀疏盲分离方法在分离高混响的欠定混叠信号中具有一定的优越性。由上述实施结果可知，本实施例提出的基于欠定卷积混叠模型的稀疏盲分离方法通过构建欠定卷积混叠模型，实现更好地、更精确地描述高混响环境下的混叠信号；通过构造稀疏代价函数，利用原信号的稀疏性更好地重构源信号；针对排序歧义性问题，通过采用方向到达角的排序方案，解决排序混乱问题，从而有效地分离高混响环境下的混叠信号。本实施例充分利用源信号的稀疏约束以及欠定卷积混叠模型的构造，在处理真实环境下的高混响混叠信号具有更高的优势。相同或相似的标号对应相同或相似的部件；附图中描述位置关系的用语仅用于示例性说明，不能理解为对本专利的限制；显然，本发明的上述实施例仅仅是为清楚地说明本发明所作的举例，而并非是对本发明的实施方式的限定。对于所属领域的普通技术人员来说，在上述说明的基础上还可以做出其它不同形式的变化或变动。这里无需也无法对所有的实施方式予以穷举。凡在本发明的精神和原则之内所作的任何修改、等同替换和改进等，均应包含在本发明权利要求的保护范围之内。当前第1页1 2 3