一种京房六十律的最优音律产生方法

本发明属于现代音乐工业领域，具体涉及一种京房六十律的最优音律产生方法。

背景技术：

在音乐艺术领域，音律是音乐实践和音乐研究的主要内容之一，五度相生律是一种音律的律制，在西方国家常常被称为毕达哥拉斯律，在古代中国被称为三分损益律，它是分别由古希腊时期的毕达哥拉斯学派和中国先秦时期的音乐家各自独立提出的，公元前7世纪，《管子·地员篇》一书提出了音律计算方法——三分损益法，几百年后的《吕氏春秋·音律篇》则在三分损益的基础上将音律增加到十二律，并试图达到“五声、六律、十二管还相为宫”的理想。而后直到西汉，律学家京房(前77～前37年)发现三分损益法在生律十一次后(即到第十二律后)不能回到出发的原律(黄钟律)上，从而给这一理想的实现造成很大障碍，因此京房按照《管子》提出的三分损益法，将十二律推演到了六十律。

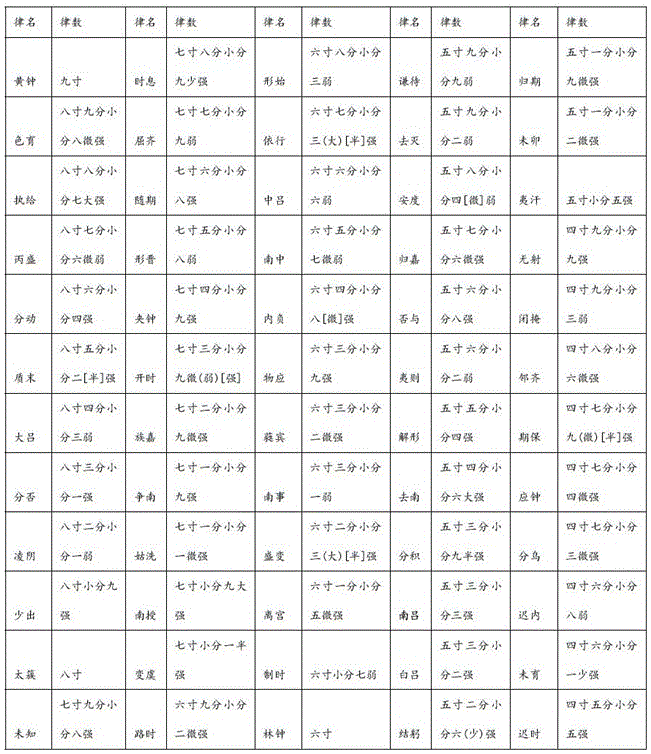
在南北朝时期范晔的《后汉书.律历志》中，记录了京房六十律的律数表示方法，每个音律的律数由二部分组成，第一部分是数字加单位，第二部分是强或弱的说明。第一部分的数字范围是“四寸五分小分五”到“九寸”，最小律数是“迟时”律，最大律数是“黄钟”律；如“分动”的律数为“八寸六分小分四强”，“凌阴”的律数为“八寸二分小分一弱”，第一部分的单位为“寸”、“分”、“小分”，在这里，一寸等于十分，一分等于十小分。第二部分的强或弱是律数的尾数部分，按尾数的大小分别用“弱”、“微弱”或“微强”、“少强”、“强”、“半强”、“大强”的表示法来表示。“强”表示多一点，“弱”表示少一点。

在京房所处的时代，“四舍五入法”概念还没出现，因此，利用“强弱”来表示无穷小数是中国古代人民的一大创举，每个音律的“强弱”怎么选择，怎么达到最优，古今中外没有文献进行过详细说明。如《后汉书.律历志》中“分动”的律数为“八寸六分小分四强”，它说明利用“三分损益法”计算出来它的值大于8.64寸，小于8.65寸，是在8.64和8.65之间的一个无穷数，这样，这个无穷数可以表示为“八寸六分小分四强”，也可以表示为“八寸六分小分五弱”，到底是用“强”表示更优还是用“弱”表示更优。京房六十律一共有60个律，各自都有不同的“强/弱”选择，构成2⁵⁹个不同的“强/弱”序列，那么哪个序列是最优的，正是本发明要解决的问题。

因此，需要一种能方便计算“强弱”的音律计算方法，从而解决“强弱”的最优分布问题。

技术实现要素：

为了弥补现有技术的不足，本发明提供一种京房六十律的最优音律产生方法的技术方案。

所述的一种京房六十律的最优音律产生方法，其特征在于包括产生系统，产生系统包括输入模块(1)、计算模块(2)和输出模块(3)，计算模块(2)包括分数音律计算单元(20)和最优小数音律值计算单元(21)，最优音律产生方法的具体步骤为：

1)通过输入模块(1)输入按实际需要给定的频率f0，频率f0作为起始律，输入需要计算的音律小数精度位数n；

2)通过分数音律计算单元(20)得到京房六十律的分数表示的数列f：从音律值为f0的起始律出发，链式生成五十九个音律，每个音律的值由前一个音律值乘以或得到，按要求生成的五十九个音律的值fi,1≤i≤59在数值范围以内，每个音律值与起始律的音律值的比例为分数式得到数列f＝{f0,f1,λ,fi,λf59},0≤i≤59；

3)通过最优小数音律值计算单元(21)得到需要计算的最优n位小数音律值数列h^*：根据数列f的每个音律值与起始律音律值的分数比，计算每个音律的n位精度位数的小数值数列g＝{g0＝f0,g1,g2,λ,gi,λ,g59}，每个小数音律值都是n位小数，省去其n位位数之后的小数部分，从而有gi≤fi＜gi+10^-n,0≤i≤59，得到六十对n位小数对{(g0,g0),(g1,g1+10^-n),(g2,g2+10^-n),λ,(gi,gi+10^-n),λ,(g59,g59+10^-n)}，从每对小数中取出一个小数，构成由六十个音律构成的数列h＝{h0＝f0,h1,h2,λ,hi,λ,h59},hi＝giorgi+10^-n，这样有2⁵⁹个不同的数列h，最优小数音律值数列h^*满足：

4)通过输出模块(3)输出最优小数音律值数列h^*。

所述的一种京房六十律的最优音律产生方法，其特征在于所述步骤2)中，通过分数音律计算单元(20)得到京房六十律的分数表示的数列f，先计算分数式xi,0≤i＜59，根据五十九个音律的值fi,1≤i≤59在数值范围的要求，音律值fi＝f0×xi,1≤i≤59，可以得出出分数式的值，其中分母的指数i的变化范围是0到59，对应的j的值分别是：[0,1,3,4,6,7,9,11,12,14,15,17,19,20,22,23,25,26,28,30,31,33,34,36,38,39,41,42,44,45,47,49,50,52,53,55,57,58,60,61,63,64,66,68,69,71,72,74,76,77,79,80,82,84,85,87,88,90,91,93]。

所述的一种京房六十律的最优音律产生方法，其特征在于所述步骤3)中，最优小数音律值数列h^*是2⁵⁹个音律数列中，相邻两个n位有限小数位的音律比例与相生法比例或者最接近的音律构成，这2⁵⁹个音律数列都有六十个音律构成，最优小数六十音律满足：

所述的一种京房六十律的最优音律产生方法，其特征在于所述输出模块(3)为显示屏。

与现有技术相比，本发明有以下优点：

本发明给出了京房六十律的最优音律构造方法，给出了京房六十律的分数式的音律计算方法。而传统的京房六十律的表示方法是人为确定的，它们的人为指定并没有达到最优效果。

附图说明

图1为现有技术中五度相生律生律方法的音律结构图；

图2为本发明中产生系统的电路关系示意图；

图3为本发明中音律律列的数列结构示意图。

具体实施方式

下面结合附图对本发明作进一步说明。

图1为京房六十律的律数(按律数大小排序)。

如图2、3所示，一种京房六十律的最优音律产生方法，包括产生系统，产生系统包括输入模块(1)、计算模块(2)和输出模块(3)，计算模块(2)包括分数音律计算单元(20)和最优小数音律值计算单元(21)，其具体步骤为：

1)通过输入模块(1)输入按实际需要人为给定的频率f0，频率f0作为起始律，输入n需要计算的音律小数精度位数；

2)通过分数音律计算单元(20)得到京房六十律的分数表示的数列f：从音律值为f0的起始律出发，链式生成五十九个音律，每个音律的值由前一个音律值乘以或得到，按要求生成的五十九个音律的值fi,1≤i≤59在数值范围以内，每个音律值与起始律的音律值的比例为分数式得到数列f＝{f0,f1,λ,fi,λf59},0≤i≤59；

3)通过最优小数音律值计算单元(21)得到需要计算的最优n位小数音律值数列h^*：根据数列f的每个音律值与起始律音律值的分数比，计算每个音律的n位精度位数的小数值数列g＝{g0＝f0,g1,g2,λ,gi,λ,g59}，每个小数音律值都是n位小数，省去其n位位数之后的小数部分，从而有gi≤fi＜gi+10^-n,0≤i≤59，得到六十对n位小数对{(g0,g0),(g1,g1+10^-n),(g2,g2+10^-n),λ,(gi,gi+10^-n),λ,(g59,g59+10^-n)}，从每对小数中取出一个小数，构成由六十个音律构成的数列h＝{h0＝f0,h1,h2,λ,hi,λ,h59},hi＝giorgi+10^-n，这样有2⁵⁹个不同的数列h，最优小数音律值数列h^*满足：

4)输出模块(3)为显示屏，通过输出模块(3)输出音律数列h^*。

通过分数音律计算单元20得到京房六十律的分数表示的数列f：先计算分数式xi,0≤i＜59，根据五十九个音律的值fi,1≤i≤59在数值范围的要求，音律值fi＝f0×xi,1≤i≤59，可以得出出分数式的值，其中分母的指数i的变化范围是0到59，对应的j的值分别是：[0,1,3,4,6,7,9,11,12,14,15,17,19,20,22,23,25,26,28,30,31,33,34,36,38,39,41,42,44,45,47,49,50,52,53,55,57,58,60,61,63,64,66,68,69,71,72,74,76,77,79,80,82,84,85,87,88,90,91,93]。

最优小数音律值计算单元(21)是用来计算最优小数音律值数列h^*，最优数列h^*是2⁵⁹个音律数列中，相邻两个n位有限小数位的音律比例与相生法比例或者最接近的音律构成，这2⁵⁹个音律数列都有六十个音律构成，六十个相邻音律满足：

本发明给出了京房六十律的最优音律构造方法，给出了京房六十律的分数式的音律计算方法。而传统的京房六十律的表示方法是人为确定的，它们的人为指定并没有达到最优效果。

本发明中的输出模块3为显示屏，本发明可应用于pc端或手机端，电脑端为例，输入模块1为键盘，计算模块2通过电脑等设备完成，输出模块3为电脑显示屏，操作时，在电脑上使用本发明的算法，然后通过键盘输入任意中心律频率f0，输入n位小数位数，然后计算模块2计算出相应的数列，并将其显示于电脑显示屏上。