一种基于Voronoi图的螺旋加工路径的生成方法与流程

本发明涉及螺旋加工路径规划的技术领域，尤其涉及一种基于Voronoi图的螺旋加工路径的生成方法。

背景技术：

Voronoi图是关于空间邻近关系的一种基础数据结构，最基本的Voronoi图是以平面点集为元素的Voronoi图，它将平面划分成凸多边形形状的Voronoi区域，平面点集中的每个元素对应区域内的任意一点到该元素的欧几里德距离比到其他元素的欧几里德距离近。因此，通过生成平面多边形轮廓的Voronoi图，规划出螺旋加工路径。

由于Voronoi图的奇妙特性，在结晶学、地质学、图形处理、机器人路径规划等领域得到了广泛应用。在数控切削加工、激光快速成型中的应用主要是用来生成螺旋加工路径。近年来,在激光快速成型中基于Voronoi图生成偏置线进而得到螺旋加工路径的研究逐渐得到重视，其主要优点有：生成Voronoi图后可在接近线性时间内生成首尾相连不需要多余环检查和求交处理的轮廓偏置线；加工线短和内向外的加工方式符合温度梯度的变化，变形翘曲小；各向同性，机械性能好。

由于Voronoi的处理数据量大、算法复杂，使得在路径规划中的应用受到限制。目前Voronoi图在螺旋加工路径中的应用还是存在如下问题：单、多连通域都采用分治算法时使得算法复杂不易实现；单、多连通域采用不同的算法将引起算法的不统一，增加实现的难度；数据结构复杂，不利于工程应用；瓶颈处峡线的判断不当使得偏置线的生成算法还不够简洁等。

技术实现要素：

本发明的目的在于克服现有技术的不足，本发明提供了一种基于Voronoi图的螺旋加工路径的生成方法，可以快速生成螺旋加工路径，显著提高加工效率和加工精度。

为了解决上述问题，本发明提出了一种基于Voronoi图的螺旋加工路径的生成方法，所述方法包括：

利用Voronoi图的Voronoi边对轮廓段的原始偏置线进行裁剪，从而得到连续轮廓段的连续偏置线；

通过找到Voronoi图中边上所有内点，在一个单调(偏置连通)域内构造一个螺旋型的加工路径；

得到平面图形的Vorinoi图和单调区域所有的内点，从而生成偏置线(环),迭代减少偏置量的大小，最终生成整个区域的螺旋加工路径。

优选地，所述利用Voronoi图的边参数方程对轮廓段的原始偏置线行裁剪，从而得到连续轮廓段的连续偏置线的步骤包括：

提出第一个新的概念，关联初始平分线：初始交点集合I中的数据项中的两个初始平分线。这两个初始平分线相交，交点是有效的候选交点；

提出第二个新的概念，非关联初始平分线：初始平分线中没有与其他初始平分线相交形成有效候选交点的初始平分线；

Voronoi图中的Voronoi边参数方程采用Voronoi边到轮廓边界的欧几里德距离t作为参数，轮廓段的原始偏置线方程也以t作为参数，从而求得原始偏置线方程与Voronoi图中的Voronoi边的交点，用这些交点裁剪原始偏置线，得到连续轮廓段的连续偏置线；

应用Voronoi边的平分线特性，避免对几何图形退化情况进行处理，进而直接得到首尾相连的有效偏置曲线。

优选地，所述通过找到Voronoi图中边上所有内点，在一个单调(偏置连通)域内构造一个螺旋型的加工路径的步骤包括：

提出第一个新的定理：与初始交点相关联的初始平分线到达内点循环次数往往比非关联的初始平分线要多；

提出第二个新的定理：当遍历不能得到所有内点时，内点必然是关联初始平分线的终点；

设非关联初始平分线双向链表集合为K、初始交点集合I中关联初始平分线集合为I’,初始平分线集合J为总集，由以上两个定理为依据来查找内点；

步骤1)如果K>0，取出链头并删除原数据，查找以该数据项终点为起点的Voronoi边，若有Voronoi边，则跳转到步骤2，无Voronoi边，存储终点，跳转到步骤1；

步骤2)判断Voronoi边起点、中点、终点的t值。若三点都单调增加，则跳转到步骤3。三点单调减少，结束本次计算，存储交点，跳转到步骤1。三点不单调，结束本次计算，存储该Voronoi边，跳转到步骤1；

步骤3)以该Voronoi边为新的起点查找相关的Voronoi边。若有Voronoi边，跳转到步骤2，无Voronoi边，存储终点，跳转到步骤1；

结束算法执行过程，至少有一个交点被保存。对被存储的交点进行后续处理：删除坐标相同的点，得到平面图形的内点。

优选地，根据加工特性确定有效的加工宽度(半径)，既偏置量的步骤包括：

根据加工特性，确定出刀具(熔宽)等直径W；

根据加工特性确定合适的加工宽度上的重叠系数ψ。并由此得到偏置量t＝(1-ψ)×W；

优选地，所述得到平面图形的Vorinoi图和单调区域所有的内点，从而生成偏置线(环),迭代减少偏置量的大小，最终生成整个区域的螺旋加工路径的步骤包括：

由内点开始，以t为偏置距离，查找共享同一个边界轮廓的两个Voronoi边；

将t带入Voronoi边的参数方程，用曲线(直线或者圆弧)连接两点，计算相应得到偏置线；

迭代上述过程，直到生成一个完整的封闭偏置环。减小偏置量，重复上述过程并最终生成整个区域的螺旋加工路径。

附图说明

为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其它的附图。

图1是本发明实施例中的一种基于Voronoi图的螺旋加工路径的生成方法流程示意图；

图2是本发明实施例中的偏置线生成方法的示例图；

图3是本发明实施例中对任意三维建模零件分层后图形的螺旋加工路径结果。

具体实施方式

图1是本发明实施例中的一种基于Voronoi图的螺旋加工路径的生成方法流程示意图。如图1所示，该方法包括：

S101，利用Voronoi图的边参数方程和轮廓段的原始偏置线方程来对原始偏置线进行裁剪，从而得到连续轮廓段的连续偏置线；

S102,在一个单调连通域内找到区域内点并由此内点开始连接偏置线得到一个封闭的加工路径环；

S103,逐步减少偏置量，最终生成覆盖整个单调区域的螺旋加工路径；

S104,查找平面多边形轮廓的所有内点，重复上述过程，得到覆盖整个平面区域的螺旋加工路径。

其中，S101包括：Voronoi图中的Voronoi边参数方程采用Voronoi边到轮廓边界的欧几里德距离作为参数。利用Voronoi边对轮廓段的原始偏置线方程进行裁剪，得到连续轮廓段的连续偏置线。应用Voronoi边的平分线特性，避免对几何图形退化情况进行处理，进而直接得到首尾相连的有效偏置曲线。

S102进一步包括：计算轮廓图中的非关联初始平分线，并用双向链表来进行存储。取出链头元素并删除原始数据，查找以该数据项终点为起点的Voronoi边。判断Voronoi边起点、中点、终点的值，并判断三点的单调性。以该Voronoi边为新的起点查找相关的Voronoi边。根据沿线宽方向上刀具直径(或激光熔宽、熔深)确定的加工宽度以及重叠系数共同得到螺旋路径生成时的偏置量。

S103进一步包括：由内点开始，以t为偏置距离，查找共享同一个边界轮廓的两个Voronoi边。将t带入Voronoi边方程，用曲线(直线或者圆弧)连接两点，计算相应得到的偏置线。迭代上述过程，直到生成一个完整的封闭偏置环。

S104进一步包括:减少偏置量，重复上述S101、S102、S103过程并最终生成整个区域的螺旋加工路径。

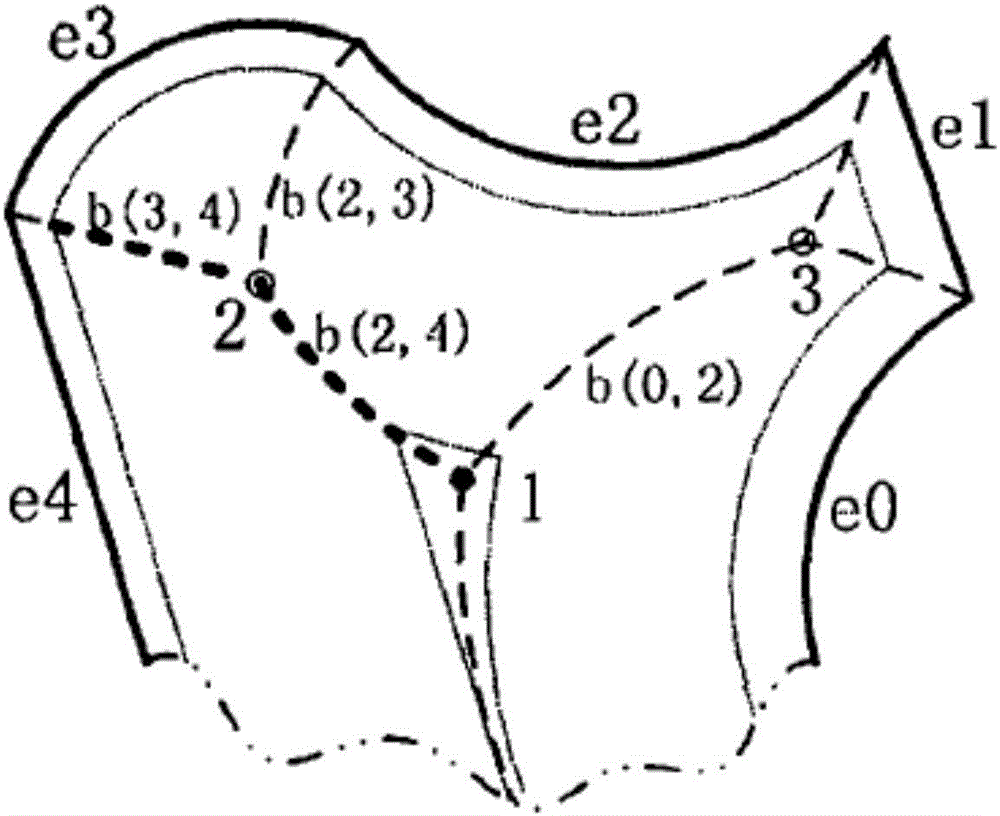
图2是本发明实施例中的偏置线生成过程的示例图，其包括：粗实线表示轮廓边界，虚线表示Voronoi图(边)，细线点表示最内层(最先)和最外层(最后)偏置环，黑实心圆点表示内点，空心圆表示Voronoi节点。以距离外边界轮廓最远的内点作为整个图形偏置的起始点，即图中的黑点1。因为内点是单调区域内偏置量t最大的平分线上的点，假设内点的偏置量为m,则m-t就对应着第一个偏置环。偏置环之间相差一个t值，由内向外，偏置量逐渐减小，最终的一个偏置量小于等于t值。同时查找共享同一个边界轮廓段Voronoi边要满足两个原则：1)边界定义元素是相同的(相同的轮廓段)；2)生成当前偏置环的t值在Voronoi边的偏置值范围内。因此，生成每个偏置环时都需要对剩余的Voronoi边进行遍历，以查找符合上述两个条件的Voronoi边。Voronoi边的t值下限就是Voronoi边节点处的t值：Voronoi边b(2,4)和b(0,2)分别在节点2、3处到达各自的偏置下限。并由此开始，由于偏置环跨越的Voronoi区增加了一个，偏置环中将增加一条偏置线。图中的偏置由1点开始，偏置量减小一个t值后生成第一个偏置环，并迭代下去，直至生成最外层的偏置环。

图3是本发明实施例中对任意三维建模零件分层后图形的螺旋加工路径结果。图中粗线条代表边界轮廓线，虚线代表Voronoi边，细点线代表螺旋加工路径。其中图a是枫叶形状图形的Voronoi图及生成的螺旋偏置线，图b是薄壁件的Voronoi图及生成的螺旋偏置线。结果表明本发明的方法是可行的。

以上对本发明实施例所提供的一种基于Voronoi图的螺旋加工路径的生成方法进行了详细介绍，本文应用了具体个例对本发明的原理及实施方式进行了阐述，以上实施例的说明只是用于帮助理解本发明的方法及其核心思想。同时，对于本领域的一般技术人员，依据本发明的思想，在具体实施方式及应用范围上均会有改变之处，综上所述，本说明书内容不应理解为对本发明的限制。