一种提升机器人铣削稳定域的方法与流程

本发明属于机器人铣削加工技术领域，具体涉及一种提升机器人铣削稳定域的方法。

背景技术：

工业机器人由于灵活性高，占地面积小和成本低等优点被广泛的应用于航空航天、模具、汽车制造等行业。但由于本身弱刚度的缺点导致其在金属切削加工过程中出现强烈的颤振现象。除了颤振振纹会对工件表面造成损害外，严重的颤振会降低工件尺寸精度，减少刀具寿命，损坏机器等。通常为了保证机器人加工不出现颤振现象，必须花费大量的时间做实验来得到一个比较好的加工条件和保守的切削参数，而这种切削参数远低于可能的加工能力，所以导致生产力的下降，同时也大大限制了工业机器人的推广和使用。旋转超声加工技术是近些年出现的一种新的加工技术，它通过将电信号转化为机械振动再传递给刀具，使其实现断续切削的效果。在加工的过程中可减小切削力、降低切削温度、减轻刀具磨损，还可以提高加工精度，延长刀具寿命等。

目前已有的基于理论分析的超声加工稳定域的求解方法，例如文献zhangy,boz,wangy,etal.effectofmachiningparametersonthestabilityofseparatedandunseparatedultrasonicvibrationoffeeddirectionassistedmilling[j].journalofmechanicalscience&technology,2017,31(2):851-858.发表了一种将超声振动作用于工件的分离型超声振动辅助铣削稳定性分析方法，考虑到了超声振动参数、加工参数和刀具结构对加工稳定性的影响。但是该模型只适用于分离型超声振动稳定性的研究，并不能用于旋转超声铣削稳定域的预测。旋转超声铣削作为一种不分离型超声振动辅助加工方法，还没有适用其稳定域的预测方法。

技术实现要素：

为了解决上述缺陷，本发明提出了一种提升机器人铣削稳定域的方法，将旋转超声加工技术与机器人铣削相结合以提升机器人铣削加工稳定域。

实现本发明目的的技术解决方案为：

一种提升机器人铣削稳定域的方法，其特征在于包括以下步骤：

步骤1、建立机器人旋转超声铣削动态切屑厚度模型；

步骤2、建立机器人旋转超声铣削动态切削力模型：根据动态切削厚度表达式由线性力模型建立切削力fr,ft,fa的表达式，然后，通过引入γ角建立单个切削刃上不断变化的切削力(fr,ft,fa)与总的切削力(fx,fy,fz)之间的映射关系，得到机器人旋转超声铣削环境下的三维动态切削力模型；

步骤3、构建机器人旋转超声铣削稳定域解析模型：将传统铣削二维稳定域解析的两自由度振动系统方程拓展至三维获得振动系统方程，再将上述步骤2建立的机器人旋转超声铣削动态切削力模型带入拓展后的振动系统方程，得到三自由度系统动力学延迟微分方程的表达式；

步骤4、求解机器人旋转超声铣削稳定域：首先离散铣削动力学延迟微分方程的周期性变化系数和时间延迟项；接着，通过cauchy变换将动力学延迟微分方程改写成一阶微分形式，并根据初始条件得到一阶动力学延迟微分方程的原始方程；然后，由动力学一阶延迟微分方程和原始方程构建机器人旋转超声铣削稳定性系数矩阵；最后，通过求解系数矩阵的特征值判断系统的状态是否稳定；

步骤5、绘制机器人旋转超声铣削颤振稳定性曲线：根据步骤1到步骤4，绘制出机器人旋转超声铣削稳定域叶瓣图，实现稳定域预测。

本发明和传统技术相比的优点为：

(1)本发明首次提出将旋转超声技术与机器人铣削相结合，大大提升了机器人铣削加工的稳定域，达到了很好的抑制颤振效果；

(2)本方法首次实现了对不分离型超声振动辅助铣削稳定域的预测，成功解决了没有适用于旋转超声铣削稳定域求解方法的问题；

(3)在机器人旋转超声铣削加工条件下，提出了用于普通立铣刀的三维稳定性分析方法，使得稳定性分析更符合铣削的实际工况；

(4)针对机器人旋转超声铣削提出了更加符合实际的动态切削厚度和动态铣削力的计算方法。

除了上面所描述的目的、特征和优点之外，本发明还有其它的目的、特征和优点。下面将参照附图，对本发明作进一步详细的说明。

附图说明

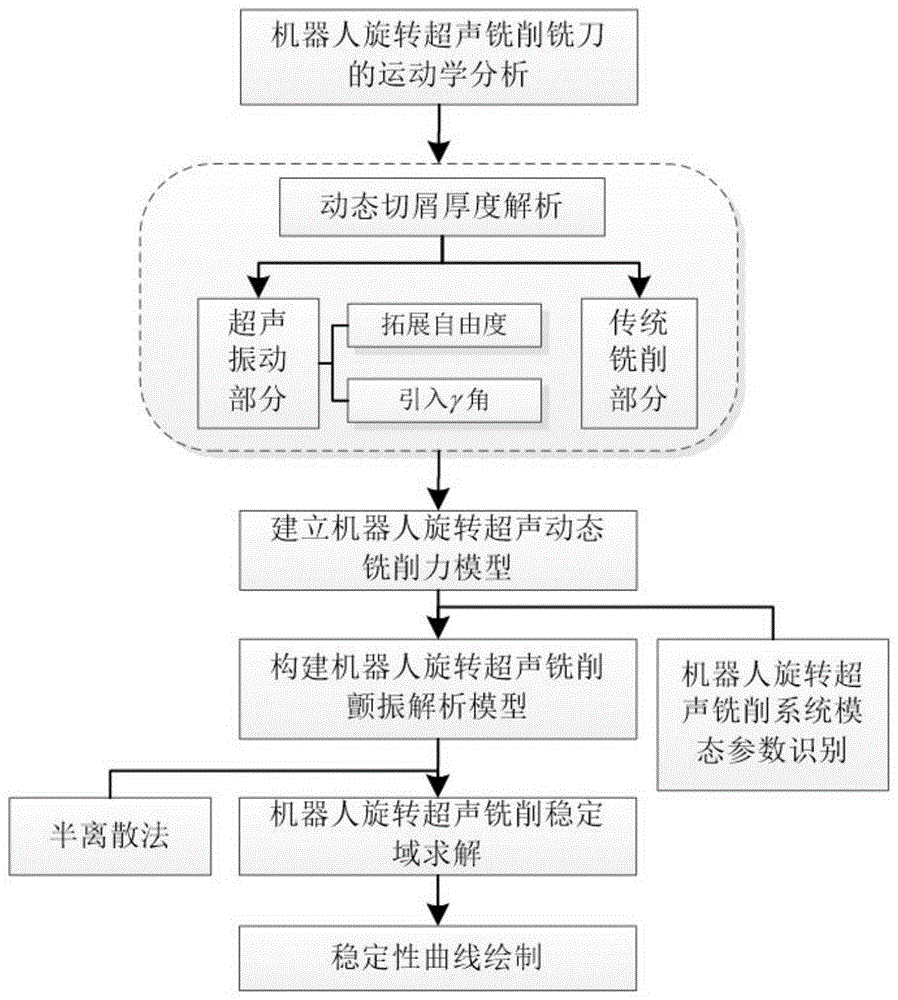
图1为本发明提升机器人铣削稳定域的方法的流程图。

图2为机器人旋转超声铣削模型主视图。

图3为机器人旋转超声铣削模型俯视图。

图4为机器人旋转超声铣削速度变化矢量图。

图5为三维动态切削厚度分析图。

图6为机器人旋转超声铣削切削力变化矢量图。

图7为机器人结构简图。

图8为机器人传统铣削前4阶模态稳定性叶瓣总图。

图9为机器人旋转超声铣削前4阶模态稳定性叶瓣总图。

图10为机器人旋转超声铣削稳定域叶瓣图。

具体实施方式

下面结合说明书附图，对本发明作进一步的说明。

图1是本发明提升机器人铣削稳定域的方法的流程图，具体包括以下步骤：

步骤1、建立机器人旋转超声铣削动态切屑厚度模型：切屑厚度包括静态和动态两个部分。依据现有的稳定性研究可以将不对稳定域有任何影响的静态部分忽略，从而只研究切屑厚度的动态部分。在使用普通立铣刀时，传统铣削稳定性研究将铣削加工简单等效为二维铣削系统得到二维切屑厚度模型。本研究在机器人旋转超声铣削条件下首次提出了使用普通立铣刀时基于三自由度铣削系统的三维切屑厚度模型。方法是通过引入一个γ角揭示了不分离型旋转超声铣削是如何影响动态切屑厚度进而影响稳定域，最终建立机器人旋转超声振动下的动态切屑厚度模型；

步骤1.1、建立机器人旋转超声铣削过程中切削刃上一点的运动学方程：包括位移方程和速度方程。如图2所示，铣刀切削刃上任意一点p的运动学方程可具体表达如下：

其中，r为刀具半径(mm)；ω是刀具转动的角速度(rad/s)；vf为进给速度(mm/s)；h0表示切削刃上的任意点p距离加工表面的高度(mm)；a是超声振动的振幅(μm)；fv为超声振动的频率(hz)；t为加工时间(s)。

步骤1.2、建立铣刀切削刃上任意点p的坐标系(xr,yc,zz)，引入超声振动作用下的角度γ。图4表示图2中铣刀切削刃上任意点p的速度矢量图。如图4所示，角度γ表示p点径向切削速度vr与z轴负方向的夹角，可以用下式表达：

其中，vz为刀具轴向振动速度，其值由公式(2)确定。vz值为正表示超声振动方向沿z轴正方向，vz值为负表示超声振动方向沿z轴负方向；为刀具径向浸入角，可以表达为：

这里ω是主轴转速(r/min)；nz是刀具齿数；j表示刀具第j个齿；λ为刀具的螺旋角。

为了简化角度γ的计算，这里我们取h0等于理论切深ap的一半。如图3所示，平均径向浸入角可表达为：

φj＝(2πω/60)·t+2π(j-1)/nz-[ap/(2r)]·tanλ(5)

步骤1.3、建立机器人旋转超声振动作用下的动态切削厚度模型。使用普通立铣刀时，传统铣削加工切削厚度是沿着铣刀径向测量的。这是因为在二自由度铣削系统中径向切削速度vr的方向与铣刀径向方向一致。而机器人旋转超声加工过程中径向切削速度vr的方向随着刀具轴向振动而不断变化，因此其动态切削厚度的测量方向不再是刀具径向，而应该是径向切削速度vr的方向。如图5所示，假设铣削加工时刀具沿x,y,z方向的动态位移分别是δx，δy,δz，将p点的动态位移向径向切削速度vr的方向投影，可得动态切削厚度的具体表达式如下：

hd＝g(φj)·[(δx·sin(φj)+δy·cos(φj))·sinγ-δz·cosγ](6)

这里，g(φj)用来判断单个刀齿是否参与切削，取值范围为0或1。当刀齿参与切削时取值为1；当刀齿不参与切削时，取值为0。

步骤2、建立机器人旋转超声铣削动态切削力模型：在三维铣削系统下，机器人旋转超声铣削的轴向振动改变了切削刃的受力方向进而改变了切削刃上切削力的方向。首先，根据动态切削厚度表达式由线性力模型建立切削力fr,ft,fa的表达式。然后，通过引入γ角建立单个切削刃上不断变化的切削力(fr,ft,fa)与总的切削力(fx,fy,fz)之间的映射关系，得到机器人旋转超声铣削环境下的三维动态切削力模型；

步骤2.1、如图6所示，建立机器人旋转超声铣削过程中切削刃上任意点p处径向力(frj)，切向力(ftj)，轴向力(faj)的表达式。传统铣削过程中，切削刃上的动态切削力正比于轴向切深和动态切削厚度。由公式(1)可知，旋转超声铣削过程中轴向切深是随着时间变化的，其实际的切深可以表示为b＝ap+as′，s′＝sin(2πfvt)。动态切削厚度由公式(6)确定。因此，单个切削刃上任意点p处的切削力可以表达为：

其中，kr，kt和ka分别为径向切削力系数、切向切削力系数和轴向切削力系数，它们的值可由槽铣实验获得。

步骤2.2：建立单个切削刃上任意点p沿x、y、z方向的切削力fxj、fyj和fzj的解析模型。如图6所示，将公式(7)中单个切削刃上一点的切削力向坐标系x、y和z方向投影，可得切削力表达式：

步骤2.3：建立x、y和z向总的切削力fx、fy和fz的解析模型。将公式(6)和(7)代入公式(8)，并对所有刀齿中的切削力求和，可得总切削力表达式：

这里，α(t)和β(t)均是三阶矩阵，可具体表达如下：

其中，

在这里，s＝sin(φj)，c＝cos(φj)，s″＝sin(γ)，c″＝cos(γ)。α(t)和β(t)满足关系β(t)＝s′α(t)，其中s′＝sin(2πfvt)。例如，

步骤3、构建机器人旋转超声铣削稳定域解析模型：将传统铣削二维稳定域解析的两自由度振动系统方程拓展至三维，再将步骤2建立的机器人旋转超声动态切削力模型带入拓展后的振动系统方程得到三自由度系统动力学延迟微分方程的表达式；

步骤3.1、根据半离散法理论，给出n维延迟微分方程的表达式。如下：

a(t+t)＝a(t)和b(t+t)＝b(t)(15)

这里，t是时间周期；τ是时间延迟。在稳定域求解的半离散法中t＝kδt。k是整数表示划分时间周期t的数量，δt是半离散的时间间隔。

步骤3.2、建立机器人旋转超声铣削三自由度振动系统方程。由传统铣削二自由度振动系统方程拓展至三维得到超声振动辅助铣削三自由度振动系统的二阶微分方程。此时，有

其中，i表示第i个时间间隔；x(t-τ)i，y(t-τ)i和z(t-τ)i表示延迟微分项；j，h和l均是三阶矩阵，可表达为：

其中，ξnx,ξny和ξnz是振动系统的阻尼比；ωnx,ωny和ωnz是振动系统的固有频率；mtx,mty和mtz是振动系统的模态质量；αxxi代表αxx,βxxi代表βxx，以此类推。

步骤4、运用半离散法求解机器人旋转超声铣削稳定域：首先离散了铣削动力学延迟微分方程的周期性变化系数和时间延迟项；接着，通过cauchy变换将动力学延迟微分方程改写成一阶微分形式，并根据初始条件得到一阶动力学延迟微分方程的原始方程；然后，由动力学一阶延迟微分方程和原始方程构建机器人旋转超声铣削稳定性系数矩阵；最后，通过求解系数矩阵的特征值判断系统的状态是否稳定；

步骤4.1、将公式(16)进行cauchy变换得到振动系统的一阶微分方程。同时，根据初始条件由一阶动力学延迟微分方程得到原始方程。一阶微分方程表达式如下：

其中，wa＝wb＝1/2；m是一个整数且m＝k＝40；ai和bi均是6阶矩阵，i表示单位矩阵，可表达如下：

和

和

同样的，根据初始条件u(ti)＝ui，原始方程ui+1可表达成：

ui+1＝piui+wariui-m+1+wbriui-m(23)

pi＝exp(aiδt)和

步骤4.2、构件铣削稳定性转移矩阵φ，根据floquet理论判断系统的稳定性。

首先，(3m+6)维的状态矩阵zi可以被表达为：

zi＝col(xiyizixiyizixi-1yi-1zi-1···xi-myi-mzi-m)(25)

这里，col是一种数学符号表示矩阵是单列矩阵。状态矩阵zi+1和zi满足以下关系：

zi+1＝dizi(26)

其中，di是(3m+6)维的系数矩阵，可以被表达为：

这里，

和g(3×6)＝[i0](28)

和

由于铣削过程刀齿切削周期τ呈周期变化，所以只需在k个离散点处对方程进行求解即可。在刀齿通过周期τ内，求取k个离散时间间隔处的表达式就可以确定铣削系统的稳定性：

φ＝dk-1dk-2···d1d0(30)

如果有一个特征值μ＞1时，铣削系统不稳定；当μ＝1时，铣削系统临界稳定；当所有特征值μ＜1时，铣削系统稳定。

步骤5、绘制机器人旋转超声铣削颤振稳定性曲线：根据步骤1到步骤4的建模过程，使用matlab软件编程绘制出机器人旋转超声铣削稳定域叶瓣图，实现稳定域预测；

机器人旋转超声铣削稳定性曲线的绘制具体流程：

(1)给定机器人旋转超声铣削系统动力学模态参数和切削力系数。动力学模态参数包括固有频率ωnx,ωny和ωnz；阻尼比ξnx,ξny和ξnz；模态质量mtx,mty和mtz。铣削力系数包括kt、kr、ka。

(2)给定进给速度vf、刀具半径r、超声振动振幅a、超声振动频率fv和刀具齿数nz；

(3)确定主轴转速ω的范围并根据加工材料的属性初定切深ap的取值范围。然后分别给出划分切深和主轴转速的间隔数量；

(4)给定离散间隔数值k，常数m，系数wa和wb确定系数矩阵di。

(5)由系数矩阵di确定转移矩阵φ，并依据转移矩阵的特征值确定铣削系统的稳定性；

(6)编写程序并运行matlab软件得到机器人旋转超声铣削稳定性叶瓣图。

实施例1

本实例以kukakr210—r2700extra工业机器人为例研究旋转超声加工技术对机器人铣削稳定域的影响，其结构简图如图7所示。该机器人铣削系统除机器人本体外还包括一个末端执行器，末端执行器中的电机带动主轴移动实现切削进给。由机器人旋转超声铣削铝合金槽铣实验计算铣削力系数，结果如表1所示。通过模态锤击实验获得机器人旋转超声铣削系统动力学模态参数如表2、表3和表4所示。现有文献表明工业机器人由于本身的弱刚性在对其进行稳定域分析时除了一阶模态，还应该考虑其它阶模态的影响。所以本发明通过分析机器人旋转超声铣削系统的前四阶模态确定该系统的稳定域。

表1铣削力系数

表2铣削系统x向模态参数

表3铣削系统y向模态参数

表4铣削系统z向模态参数

取刀具齿数nf为3、超声振动频率fv为20khz和超声振动振幅a为0/10μm，振幅为0时表示没有引入旋转超声即为机器人传统铣削。通过以上所述预测方法，计算并绘制了超声振动振幅a分别为0/10μm的各阶模态(1,2,3,4)的稳定性曲线，如图8和9所示。若要保证机器人旋转超声铣削过程中不发生颤振，应当保证在各阶模态下铣削状态都是稳定的。因此，我们分别取图8和9中各阶模态叶瓣图曲线最低点构成新的稳定性曲线并将其作为机器人铣削的稳定域，结果如图10所示。可以发现，在传统机器人铣削加工中引入超声振动后铣削稳定域得到非常明显的提升。因此，将旋转超声加工技术与机器人铣削相结合是提升机器人加工稳定域的有效途径。

以上所述仅为本发明的优选实施例而已，并不用于限制本发明，对于本领域的技术人员来说，本发明可以有各种更改和变化。凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。