一种摆线齿锥齿轮端铣刀盘刀刃曲线优化方法与流程

本发明属于摆线齿锥齿轮加工领域，具体为一种摆线齿锥齿轮端铣刀盘刀刃曲线优化方法。

背景技术：

摆线齿锥齿轮因其产形轮齿线为延伸外摆线而得名，它采用等高齿制，以平面产形轮原理连续分度法(face-hobbing)铣齿加工。摆线齿锥齿轮齿制有三种：德国克林贝格制(klingelnberg)、瑞士奥利康制(oerlikon)和美国格里森制(gleason)，分别简称克制、奥制和格制。

摆线齿锥齿轮假想平面产形轮产形面的成形原理：刀盘和产形轮各有一个滚圆，刀盘相对于产形轮的运动可看作是刀盘滚圆在产形轮滚圆上作纯滚动，即刀盘滚圆直径与产形轮滚圆直径的比等于刀盘刀齿组数和产形轮齿数的比。当刀盘滚圆在产形轮滚圆上纯滚动时，刀刃相对于产形轮扫出的曲面即为产形轮齿面，刀刃上的点在产形轮平面内的轨迹为延伸外摆线。被加工齿轮的齿面由产形轮齿面包络而成。实际加工中，用机床摇盘代表产形轮，其刀盘刀齿分为若干组，每组至少有一个内刀和一个外刀，分别加工被加工齿轮的凸面和凹面。摆线齿锥齿轮理论上可以加工出完全共轭的齿轮副，但为了实现实际要求的局部接触，克制采用机械结构极为复杂的分体式双层刀盘，奥制和格制则采用整体刀盘与刀倾机构，后两者的计算均及其繁复。为更好的控制齿面接触区，三种齿制都引入圆弧切削刃来进行齿高方向修形，与齿长方向鼓形相结合，使齿面失配更加合理可控。

近年来，克林贝格和格里森都开发了六轴全数控锥齿轮机床，取消了摇盘机构，采用硬质合金尖齿条整体刀盘刀倾法加工摆线齿锥齿轮，部分机床可高速干切，但克林贝格双层刀盘结构复杂，设计加工困难，目前只有克林贝格自己可以制造；奥利康和格里森的尖齿刀盘设计与加工精度要求特别高，需要专门的磨刀机与检刀机。实际加工中常用切削刃廓形以直线和圆弧为主，在少数情形下，为避免齿顶接触增加刀顶凸角来进行齿根修形，且通常是对小轮进行的，这将进一步降低小轮齿根强度。采用直线刀刃加工的齿轮，当有安装误差或受载变形后，极易产生齿顶齿根接触，即便以圆弧代替了直线，由于通常圆弧半径很大(>1000mm)，并不能改善齿顶齿根接触的状况。采用刀顶凸角可以消除这一现象，但有两方面的缺陷：一是给定刀顶凸角和修形量的盲目性，需要反复切削试验寻求合理值；二是刀顶凸角是一段直线，在与主刀刃接点处各阶导数均不连续，即这是一种硬性的齿面修形，对齿面接触是不利的。

技术实现要素：

本发明的目的在于克服上述现有技术中解决齿顶齿根接触的问题不能保证齿面接触特性的缺点，提供一种摆线齿锥齿轮端铣刀盘刀刃曲线优化方法。

一种摆线齿锥齿轮端铣刀盘刀刃曲线优化方法，该方法包括下述步骤：

1)根据齿轮副参数和刀具基本参数确定刀齿切削刃分段及各段曲线形式；

所述刀齿切削刃包括主切削刃、齿顶修形、齿根修形、刀尖圆角与刀顶刃，以上各段曲线的节点相切；

2)确定大轮齿顶啮合起始边界；

3)求步骤2)中大轮修形边界对应的一系列小轮理论齿面点，并将它作为小轮齿根理论修形边界；

所述小轮理论齿面为与大轮齿面完全共轭的小轮齿面；

4)确定小轮刀齿齿根修形高度或者确定齿根修形高度和齿顶修形高度；

5)根据节点相切条件和齿形修形量，计算刀刃齿顶的曲率半径或/和齿根修形的曲率半径；

6)确定刀尖圆角半径。

进一步的，步骤2)中所述的大轮齿顶啮合起始边界为大轮齿面上的一条接触区上边界，为平行于齿顶的一条直线。

进一步的，步骤4)中确定小轮刀齿齿顶修形高度的具体过程为：

求步骤3)中小轮理论边界点对应的实际小轮齿面点的刀刃曲线参数集合，取其最小值；

所述最小值在小轮齿面上的一系列对应点即小轮齿根实际修形边界，所述边界到刀顶线的距离即为小轮刀齿齿顶修形高度。

进一步的，步骤4)中确定小轮刀齿齿根修形高度的具体过程为：

求所述小轮齿顶理论修形边界对应的小轮齿面点刀刃曲线参数集合，取其最大值；

所述最大值在小轮齿面上的对应轨迹为小轮齿顶实际修形边界，所述小轮齿顶实际修形边界到刀齿根部的距离即为小轮刀齿齿根修形高度。

进一步的，所述小轮理论边界通过旋转投影来确定小轮实际修形边界。

进一步的，根据受刀顶宽和顶刃倾角，通过试错法求刀尖圆角半径的最大值。

进一步的，求得的最大刀尖圆角半径满足：

最大刀尖圆角半径不能造成过度旁切，即切齿时副切削刃的刀尖不能切到齿槽另一侧的齿面；

最大刀尖圆角半径应保证齿根过度曲面不能与配对齿轮的齿顶发生干涉。

与现有技术相比，本发明具有以下有益效果：

本发明的摆线齿锥齿轮端铣刀盘刀刃曲线优化方法，在保证齿面接触特性的前提下能够更合理的消除齿顶齿根接触，从齿轮副啮合原理出发直接设计接触区域，解决了现行方法给定刀顶凸角和修形量的盲目性，不再需要反复试切，在设计阶段能够在保证齿面接触特性的前提下更合理的消除齿顶齿根接触；本发明的摆线齿锥齿轮端铣刀盘刀刃曲线优化方法，不仅适用于摆线齿锥齿轮，也适用于其它用端铣刀盘加工的齿轮的刀齿切削刃的优化。

附图说明

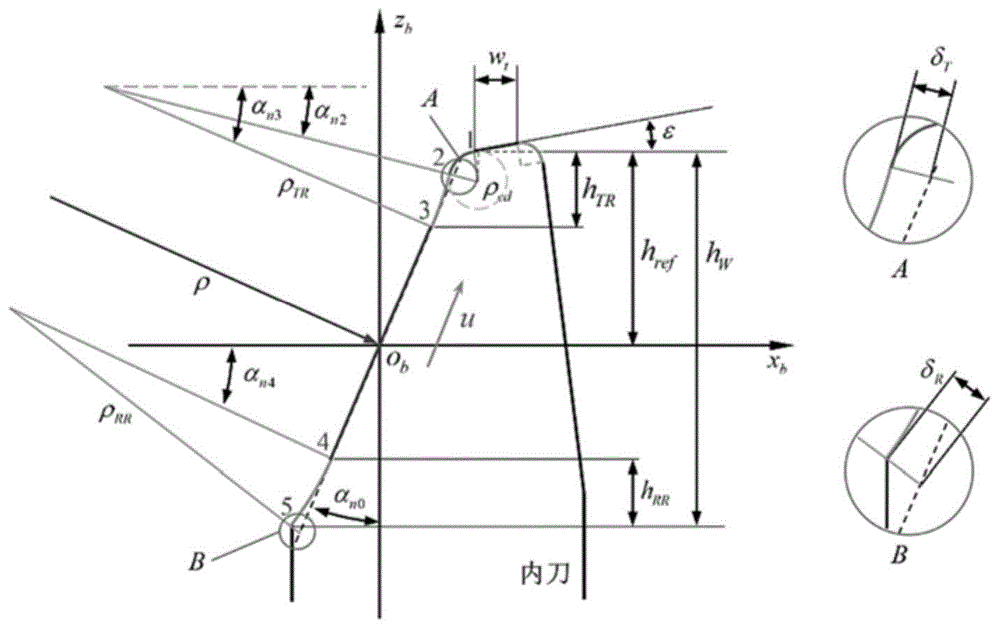
图1为本发明内刀齿切削刃分段优化模型；

图2为本发明的大轮齿顶理论啮合边界；

图3为本发明的小轮齿根修形边界；

图4为本发明的小轮齿顶修形边界；

图5为本发明的刀顶旁切与过渡曲面干涉示意图；其中，5(a)为刀顶旁切，5(b)为过渡曲面干涩；

图6为实施例中左旋小轮刀盘的刀齿法截形优化结果。

具体实施方式

为了使本技术领域的人员更好地理解本发明方案，下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分的实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都应当属于本发明保护的范围。

需要说明的是，本发明的说明书和权利要求书及上述附图中的术语“第一”、“第二”等是用于区别类似的对象，而不必用于描述特定的顺序或先后次序。应该理解这样使用的数据在适当情况下可以互换，以便这里描述的本发明的实施例能够以除了在这里图示或描述的那些以外的顺序实施。此外，术语“包括”和“具有”以及他们的任何变形，意图在于覆盖不排他的包含，例如，包含了一系列步骤或单元的过程、方法、系统、产品或设备不必限于清楚地列出的那些步骤或单元，而是可包括没有清楚地列出的或对于这些过程、方法、产品或设备固有的其它步骤或单元。

下面结合附图对本发明做进一步详细描述：

一种摆线齿锥齿轮端铣刀盘刀刃曲线优化方法，包括以下步骤：

1)确定刀齿切削刃分段及各段曲线形式

参见图1，图1为本发明内刀齿切削刃分段优化模型，图中，htr、hrr分别为刀片的齿顶和齿根修形高度，相应的修形量分别是δt和δr，ε为顶刃倾角，wt为刀顶宽；

在刀盘法截面内，以刀齿参考点为原点，设刀片坐标系sb-xyz，u为刀刃曲线参数，指向刀顶方向为正，基于几何关系，刀刃各部分的函数表达式如下：

a)主切削刃：

b)齿顶修形

c)齿根修形

d)刀尖圆角

上式中，刀具齿形角αn0、刀齿参考点的高度href和主刀刃曲率半径ρ是在齿面设计时由参考点的位置和接触特性决定的；

各节点齿形角及各段弧长计算公式如下：

各节点齿形角：

各段弧长：

2)确定大轮齿顶啮合起始边界

见图2，图2为本发明的大轮齿顶理论啮合边界，在大轮齿面上确定一条接触区上边界，通常为平行于齿顶的直线，δg1为起始边界到大轮齿顶的距离；

3)计算小轮齿根的理论修形边界

求解步骤2)中大轮修形边界对应的一系列小轮理论齿面点并将它作为小轮齿根理论修形边界，小轮理论齿面为与大轮齿面完全共轭的小轮齿面，见图3，图3为本发明的小轮齿根修形边界，菱形线是由大轮修形边界共轭求出的小轮理论修形边界，倒三角线是刀刃曲线分段节点实际划出的小轮齿面边界；

4)确定小轮刀齿齿顶修形高度htr

求解步骤3)中小轮理论边界点对应的实际小轮齿面点的u参数集合utr，取其最小值umin，它在小轮齿面上的一系列对应点即小轮齿根实际修形边界，见图3，图3为本发明的小轮齿根修形边界，该点到刀顶线的距离即为htr；

5)确定小轮刀齿齿根修形高度hrr

用步骤2)中的方法确定一条小轮齿顶理论修形边界，见图4，图4为本发明的小轮齿顶修形边界，实线为选定的小轮齿顶理论修形边界，菱形线为刀具切削刃节点划出的小轮齿面实际边界；

求该边界对应的小轮齿面点u参数集合urr，其最大值umax，它在小轮齿面上的对应轨迹为小轮齿顶实际修形边界，该点到刀齿根部的距离即为hrr；

6)计根据节点相切条件和齿形修形量计算刀刃齿顶与齿根修形的曲率半径ρtr和ρrr；

7)确定刀尖圆角半径ρed

刀尖圆角半径不能直接计算，应满足：不能造成过度旁切，即切齿时副切削刃的刀尖不能切到齿槽另一侧的齿面，见图5(a)，图5(a)为刀顶旁切；保证齿根过度曲面不能与配对齿轮的齿顶发生干涉，见图5(b)，图5(b)为过渡曲面干涉。

实施例1

按上述方法针对一摆线齿准双曲面齿轮副进行切削刃优化，齿轮副参数为：轴交角σ＝90°，偏置距av＝30mm，大小轮齿数z1/z2＝10/37，大轮外节圆直径d02＝469mm，中点螺旋角βm2＝34°，平均压力角αn＝22.5°，齿宽b2＝70mm；刀具基本参数：刀盘半径rc＝175mm，刀盘头数z0＝17，刀具齿形角αnd/αnc＝21°/23.5°。

具体实施如下：

1)选定只对小轮进行修缘，且齿顶齿根都修缘；

2)取大轮轮齿顶啮合边界到齿顶的距离δg1＝2mm，小轮齿顶修形量δt＝0.25mm，齿根修形量为δr＝0.15mm；

3)计算得小轮齿根修形的刀刃参数umin和刀刃修形高度htr分别为：

内刀齿：umini＝7.33，htri＝4.64mm

外刀齿：umine＝7.68，htre＝4.37mm

4)取小轮齿顶修形高度为3mm，计算得小轮齿顶修形的刀刃参数umax和刀刃修形高度hrr分别为：

内刀齿：umaxi＝-4.24，hrri＝6.39mm

外刀齿：umaxe＝-4.55，hrre＝7.02mm

5)根据节点相切条件和齿形修形量δt和δr，计算刀刃齿顶与齿根修形的曲率半径ρtr和ρrr：

内刀齿：ρtri＝42mm，ρrri＝53mm

外刀齿：ρtre＝40mm，ρrre＝72mm

6)确定刀尖圆角半径，为保证刀尖强度取ρedi＝ρede＝1.8mm。

7)采用无刀顶倾角的刀齿形式，将所有参数代入到步骤1)中的刀刃曲线模型，最终确定的小轮刀齿切削刃的法截形如图6所示，图6为实施例中左旋小轮刀盘的刀齿法截形优化结果，本例对小轮的凹凸面均进行了齿顶和齿根修缘，大轮无需修缘，有效避免了齿顶齿根接触，又降低了大小轮刀具修磨检验的难度，对实际加工意义重大。

以上内容仅为说明本发明的技术思想，不能以此限定本发明的保护范围，凡是按照本发明提出的技术思想，在技术方案基础上所做的任何改动，均落入本发明权利要求书的保护范围之内。