电阻焊中的飞溅探测方法及其装置与流程

1.本发明涉及一种通过利用一对电极对将多个金属板重叠而成的工件一边进行加压一边进行通电来将该多个金属板进行焊接的电阻焊中的飞溅探测方法及其装置。


背景技术：

2.以点焊为代表的电阻焊多用于车体的组装等。在点焊中，利用一对棒状电极对将多个金属板重叠而成的工件一边进行加压一边进行通电。因通过该通电所产生的焦耳热，该多个金属板在其接触部熔解并凝固，从而被焊接。此时，根据焊接条件，有时焊接部的温度过于上升而产生熔融物飞散的飞溅现象。如果产生该飞溅，则无法得到预期的焊接强度，另外，还有时飞散的熔融物附着于焊接部的周边，需要进行后处理。
3.关于防止飞溅的产生，在专利文献1中记载了：在螺母凸焊中，在一对焊接用电极的位移量超过规定的阈值时，使焊接电流上升。在产生螺母的突起的熔化而接触面积扩大之后使焊接电流上升，由此抑制飞溅的产生。
4.现有技术文献
5.专利文献
6.专利文献1：日本特开2014
‑
217854号公报


技术实现要素：

7.发明要解决的问题
8.如果根据工件适当地设定焊接电流等焊接条件，则能够抑制飞溅的产生。为此，以探测在当前焊接条件下是否产生飞溅、或者产生飞溅的可能性是否高为前提。关于飞溅的产生，由作业者观察焊接状态就能够确认，但是在大量的工件流动的生产线上，一个一个地通过目视来确认飞溅的产生并不容易。
9.对此，考虑着眼于由于飞溅的产生而工件的焊接部位的厚度变薄的现象，基于焊接中的一对电极间距离的减少量来探测飞溅。但是，在对工件的焊接部位进行了加压时在焊枪上产生挠曲，因此难以以高精度检测其电极间距离的减少量。
10.因此，本发明提出了电阻焊中的新的飞溅探测方法及其装置。
11.用于解决问题的方案
12.本发明为了解决上述问题，在飞溅的探测中采用不受焊枪的挠曲影响的电极间的通电电阻，利用统计方法探测飞溅。
13.在此公开的飞溅探测方法是一种电阻焊中的飞溅探测方法，上述电阻焊是通过利用一对电极对将多个金属板重叠而成的工件一边进行加压一边进行通电，来将上述多个金属板进行焊接的电阻焊，上述电阻焊中的飞溅探测方法的特征在于，具备以下步骤：
14.在规定的焊接条件下的各焊接中隔着规定时间间隔检测上述一对电极间的通电电阻下降量，累积与该通电电阻下降量有关的数据；
15.基于上述数据计算该焊接条件下的上述通电电阻下降量的频数分布；
16.利用高斯函数对上述频数分布进行拟合，根据该拟合是否在统计上显著，来判定该焊接条件下的飞溅的产生。
17.另外，在此公开的飞溅探测装置是一种电阻焊中的飞溅探测装置，上述电阻焊是通过利用一对电极对将多个金属板重叠而成的工件一边进行加压一边进行通电，来将上述多个金属板进行焊接，上述电阻焊中的飞溅探测装置的特征在于，具备：数据累积单元，在规定的焊接条件下的各焊接中隔着规定时间间隔检测上述一对电极间的通电电阻下降量，累积与该通电电阻下降量有关的数据；频数分布计算单元，基于上述数据累积单元的数据计算该焊接条件下的上述通电电阻下降量的频数分布；以及判定单元，利用概率密度函数对由上述频数分布计算单元计算的频数分布进行拟合，根据该拟合是否在统计上显著，来判定该焊接条件下的飞溅的产生。
18.在上述电阻焊中，随着焊接的进展，金属板其温度上升而逐渐软化并熔融。因此，电极与金属板的接触面积增大，随之通电电阻(一对电极间的电阻)逐渐下降。在飞溅产生时，由于熔融物的飞散而金属板的厚度局部性地变薄，因此上述通电电阻下降量暂时变大。因而，考虑监视该通电电阻下降量来探测飞溅。但是，飞溅的产生时机不是固定的，另外，通电电阻下降量也各不相同，无法唯一地设置阈值。
19.因此，在本发明中，求出上述通电电阻下降量的频数分布，利用高斯函数对其进行拟合，根据该拟合是否在统计上显著，来判定飞溅的产生。即，如果是无飞溅的产生的正常焊接，则可认为通电电阻下降量的频数分布遵循一个高斯分布。于是，在利用高斯函数对实际的频数分布进行了拟合时，如果存在飞溅的产生，则该拟合的显著性变低。因此，根据该拟合是否在统计上显著，来判定飞溅的产生。
20.在上述飞溅探测方法及其装置中，在一个实施方式中，隔着上述规定时间间隔检测的通电电阻下降量是该规定时间内的通电电阻下降量。由此，能够可靠地捕捉由于飞溅的产生而通电电阻大幅下降的现象。
21.在上述飞溅探测方法及其装置中，在一个实施方式中，针对上述频数分布，进行利用1个高斯函数的拟合和利用2个高斯函数的拟合，在利用2个高斯函数的拟合在统计上更显著时，判定为该焊接条件下的飞溅的产生度高。
22.在产生了飞溅时，与未产生飞溅时相比，通电电阻下降量变大。因此，如果将通电电阻下降量的频数分布设为直方图，则容易带有双峰性。即，容易成为在通电电阻下降量相对大的部位和通电电阻下降量相对小的部位具有峰的形状。其结果，在产生飞溅的焊接条件下，利用2个高斯函数的拟合在统计上显著。因而，能够根据利用1个高斯函数的拟合和利用2个高斯函数的拟合中的哪一个相对显著来判定飞溅的产生。
23.在上述飞溅探测方法及其装置中，在一个实施方式中，在利用2个高斯函数的拟合在统计上更显著、且该2个高斯函数各自的平均值之差为规定值以上时，判定为属于该2个高斯函数中的平均值更大的高斯分布(高斯函数)的概率高的通电电阻下降量是由于飞溅的产生而引起的。
24.在上述飞溅探测方法及其装置中，在一个实施方式中，在利用1个高斯函数的拟合在统计上更显著时，以及利用2个高斯函数的拟合在统计上更显著、但该2个高斯函数的各高斯函数的平均值之差小于规定值时，通过卡方检验来判定有无产生飞溅。
25.即，针对隔着上述规定时间间隔检测的各通电电阻下降量计算卡方值，判定为与
比由卡方分布决定的规定阈值大的卡方值有关的通电电阻下降量是由于飞溅的产生而引起的。由于是基于卡方统计量的飞溅判定，因此其判定精度变高。
26.发明的效果
27.根据本发明，在规定的焊接条件下的各焊接中隔着规定时间间隔检测电极间的通电电阻下降量，根据与该通电电阻下降量有关的数据求出通电电阻下降量的频数分布，利用高斯函数对该频数分布进行拟合，根据该拟合是否在统计上显著，来判定该焊接条件下的飞溅的产生，因此能够不受例如焊接时的焊枪的挠曲那样的干扰的影响而高精度地探测飞溅的产生。
附图说明
28.图1是表示电阻焊装置的飞溅探测装置的结构图。
29.图2是示意性地表示正常焊接时与飞溅产生时的通电电阻的变化的曲线图。
30.图3是表示通电电阻下降量的直方图的一例的图。
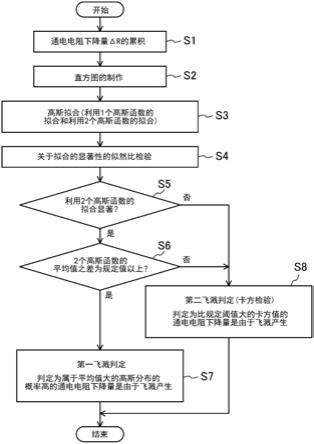
31.图4是表示飞溅探测的流程的图。
32.图5是表示涉及拟合的2个高斯函数的平均值之差的直方图的图。
33.图6是表示通电电阻下降量的直方图的其它例的图。
34.图7是涉及拟合的2个高斯函数局部重叠的说明的曲线图。
35.图8是表示卡方值的直方图的一例的图。
具体实施方式
36.以下，基于图来说明用于实施本发明的方式。以下的优选实施方式的说明本质上只不过是例示，并不意图限制本发明、其应用物或者其用途。
37.<电阻焊中的飞溅探测装置的整体结构>
38.图1所示的作为电阻焊装置的点焊装置1例如配置于生产线，通过利用一对电极对将多个金属板重叠而成的工件w一边进行加压一边进行通电，来将上述多个金属板进行焊接。
39.点焊装置1具备焊枪11、保持焊枪11的臂型机器人12、机器人控制装置13以及焊接控制装置(计时器)14。机器人控制装置13对焊枪11的工作和机器人12的工作进行控制。焊接控制装置14控制流通焊接电流的时间和电流的大小，并且监视流过的电流的时间和大小。在该焊接控制装置14上连接有飞溅探测装置15。飞溅探测装置15基于与后述的通电电阻下降量有关的数据探测在焊接中熔融物飞散的飞溅的产生。
40.焊枪11是c型焊枪，具备臂16、设置于臂16的一对相对的电极(固定电极17和可动电极18)、以及对可动电极18进行驱动的伺服马达19。对于伺服马达19，由机器人控制装置13进行控制。
41.机器人12是具有6个关节轴j1～j6的多关节机器人。该机器人12在底座21上具备旋转部22、下部臂23、上部臂24、第一～第三顶端部25～27等，它们构成为能够相互转动。机器人12具备将各构件绕各关节轴j1～j6进行驱动的伺服马达。对于这些伺服马达，由机器人控制装置13进行控制。
42.焊接控制装置14基于从机器人控制装置13接收的焊接条件、焊接指令，在工件w被
电极17、18以规定加压力夹持的状态下，从电极17、18对工件流通被控制的焊接电流。在通电结束后，焊接完成信号从焊接控制装置14被送到机器人控制装置13。
43.飞溅探测装置15具备数据累积单元31、频数分布计算单元32以及判定单元33，由包括微型计算机的电子电路构成。
44.数据累积单元31基于由焊接控制装置14控制的焊接中的电极17、18间的电压和焊接电流，求出电极17、18间的通电电阻的经时变化数据，隔着规定时间间隔检测规定的微小时间内的通电电阻的下降量，逐渐累积与该通电电阻下降量有关的数据。总之，如图2所示，随着焊接的进展，通电电阻下降，因此检测其下降量。
45.在本实施方式中，在焊接中按每个规定时间δt基于该规定时间的前后的电阻值计算通电电阻下降量δr(δr1、δr2、δr3、
……
)，逐渐累积与相同的焊接条件下的各焊接中的通电电阻下降量δr有关的数据。在各种焊接条件下获取这样的数据。在此，关于通电电阻下降量δr的检测，在利用电极17、18的通电开始当初由于接触电阻而通电电阻的下降急剧，因此优选的是，从自通电开始起经过数十msec后通电电阻的下降稳定的时间点起获取与通电电阻下降量δr有关的数据。
46.频数分布计算单元32基于数据累积单元31的数据计算相关焊接条件下的通电电阻下降量δr的频数分布。图3表示作为频数分布的直方图的一例。判定单元33基于上述频数分布，利用统计方法判定相关焊接条件下的飞溅的产生。
47.接着，参照图3～图7来具体说明利用飞溅探测装置15的飞溅探测方法。
48.如图4所示，飞溅探测方法由数据累积单元31的步骤s1的处理、频数分布计算单元32的步骤s2的处理以及判定单元33的步骤s3～s8的处理构成。
49.在步骤s1中，累积相同焊接条件下的各焊接中的通电电阻下降量δr。
50.在步骤s2中，基于上述累积的通电电阻下降量δr的数据，制作图3中示出一例的、以通电电阻下降量为横轴、以频数为纵轴的直方图。
51.在步骤s3中，对直方图进行高斯拟合。即，进行利用1个高斯函数的拟合gmm1和利用2个高斯函数的拟合gmm2。在图3的例子中，a是利用1个高斯函数拟合的高斯分布曲线，b是利用2个高斯函数拟合的高斯分布曲线。
52.在步骤s4中，关于上述gmm1、gmm2模型的哪一个更好地再现数据的分布，进行似然比检验。即，根据将
‑
2乘以在该拟合中估计出参数的最大对数似然所得到的
‑
2log(l)of gmm1和
‑
2log(l)of gmm2，求出2个模型的似然比
‑
2log(deltal)。
53.在图3的例子中，成为与
‑
2log(l)of gmm1相比
‑
2log(l)of gmm2的值小这样的结果。因而，2个高斯函数的模型gmm2更适合。gmm1模型与gmm2模型的似然比
‑
2log(deltal)为约285。似然比在当前情况下近似地遵循自由度为3的卡方分布，因此能够计算使似然比
‑
2log(deltal)成为这样的值的概率p值(p
‑
value)。在本例的情况下，成为p值小于规定的显著水平1
×
10
‑4这样的结果，因此2个高斯函数的模型与1个高斯函数的模型相比在统计上更显著地再现数据的分布。
54.在接下来的步骤s5中，在判定为利用2个高斯函数的拟合在统计上显著时，进入步骤s6，判定2个高斯函数的平均值μ1、μ2之差是否为规定值以上。
55.如之前叙述的那样，在产生飞溅时，在将通电电阻下降量的频数分布设为直方图时容易带有双峰性，因此能够基于这2个峰位置之差适当地设定规定值。或者，如图5所示，
当关于峰位置之差、即平均值μ1、μ2之差制作直方图时，成为该差为“8”的附近成为谷的双峰型的曲线。在该情况下可以说，作为规定值，优选采用7～9附近的值。
56.在2个高斯函数的平均值μ1、μ2之差为规定值以上时，进入步骤s7的第一飞溅判定。即，判定为属于平均值更大的高斯分布的概率高的通电电阻下降量是由于飞溅的产生而引起的。
57.在图6中示出该事例的直方图和拟合。在该例子中，平均值μ1、μ2之差为约23，得到独立的2个高斯分布曲线b1、b2。判定为属于平均值更大(该图右侧)的高斯分布(高斯函数)的各通电电阻下降量δr是由于飞溅的产生而引起的。
58.如图7所示，在2个高斯分布曲线b1、b2局部重叠时，根据属于哪个高斯分布的概率高，来判定是否为与飞溅的产生有关的通电电阻下降量。例如，就通电电阻下降量δra而言，属于b1的概率高于属于b2的概率，因此判定为是正常焊接中的通电电阻的下降。与此相对，就通电电阻下降量δrb而言，属于b2的概率高于属于b1的概率，因此判定为是因飞溅的产生引起的通电电阻的下降。
59.另一方面，在步骤s5的判定为“否”(利用1个高斯函数的拟合显著)时以及步骤s6的判定为“否”(2个高斯函数的平均值之差小于规定值(图3的事例：该平均值之差为约3.6))时，进入步骤s8的第二飞溅判定。
60.第二飞溅判定是基于卡方值检验的飞溅判定，针对一个一个的电阻波形计算卡方值。在此，例如假定以n＝20周期的通电时间进行了焊接。首先，利用基于该焊接条件的全部的通电电阻的经时变化数据(例如2000个)，求出第一个周期的通电电阻下降量δr1。然后，求出其样品的样本均值δr1_ave和方差δr1_σ，计算(δr1i
‑
δr1_ave)2/δr1_σ2。针对δr2、δr3、
……
、δrn也同样地计算。最后将它们相加，根据一个电阻波形数据计算卡方统计量。
61.图8是所得到的卡方值的直方图，c是自由度为20的卡方分布的理论曲线。在该图的情况下，99.99％的百分点的值为约52.4，将具有超过该阈值的卡方值的电阻波形判定为飞溅。
62.如以上，根据本实施方式，根据与焊接时的通电电阻下降量有关的数据以统计方式探测飞溅的产生，因此能够不受如焊接时的焊枪的挠曲那样的干扰的影响而高精度地探测飞溅的产生。
63.附图标记说明
64.1：点焊装置
65.11：焊枪
66.14：焊接控制装置(计时器)
67.15：飞溅探测装置
68.17：电极
69.18：电极
70.31：数据累积单元
71.32：频数分布计算单元
72.33：判定单元
73.w：工件