高速数控鞋楦加工倾斜刃圆环铣刀及优化设计方法

1.本发明涉及高速数控鞋楦加工领域，具体涉及一种高速数控鞋楦加工倾斜刃圆环铣刀及优化设计方法。


背景技术：

2.目前，数控机床机械加工使用的刀具主要有球头刀、平底刀、圆环刀、圆锥刀、鼓形刀和圆柱刀等。圆环铣刀容易实现高的加工线速度，加工效率远远高于其他刀具，广泛应用于鞋楦模具的加工。
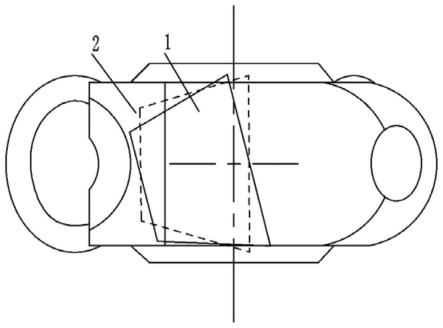
3.现有加工鞋楦的圆环铣刀为准圆环铣刀，由刀体和刀片组成，刀片为圆锥体，大端为刀刃。由于受刀具结构限制，同时要考虑其磨损，所以铣刀刀刃所在平面未过刀具回转轴线。如图1、图2所示，刀刃所在平面与刀具回转轴线存在距离h，此时所形成的刀具母线为椭圆。而利用现有准圆环铣刀在编制鞋楦数控加工程序时，若按照刀具母线为椭圆进行编程则计算量大、编程复杂，一般仍然将其视为标准圆环铣刀编程，导致存在误差，因此称这种铣刀为准圆环铣刀。


技术实现要素：

4.本发明提出一种高速数控鞋楦加工倾斜刃圆环铣刀的优化设计方法，以降低现有的准圆环铣刀由于铣刀刀刃所在平面安装未过刀具回转轴线导致的加工误差。
5.本发明解决上述问题的技术方案是：一种高速数控鞋楦加工倾斜刃圆环铣刀的设计方法，基于准圆环铣刀进行优化，所述准圆环铣刀包括铣刀刀片和刀体；所述铣刀刀片刃所在平面未过刀具几何中心，所述铣刀刀片逆时针偏置h；其特殊之处在于，包括以下步骤：
6.s1：将准圆环铣刀的铣刀刀片绕刀具径向旋转一定角度；
7.s2：推导出倾斜刃圆环铣刀的母线方程和刀刃包络面母线方程；
8.s3：得到倾斜刃圆环铣刀的母线与拟合出的标准圆之间的误差；
9.s4：优化得出一组误差最小时的旋转轴位置和旋转角度。
10.进一步地，上述步骤s1具体包括：
11.将准圆环铣刀的铣刀刀片绕刀具径向旋转一定角度θ，建立铣刀刀片的刀刃包络面的三维模型，设圆环铣刀简化模型的铣刀刀片旋转一周的中心o
t
为坐标原点，以左手法则建立坐标系o
t-x
tytzt
，其中铣刀刀片中心点到o
t
的距离为r，r是铣刀刀片中心所在的圆的半径；x
totyt
平面与铣刀刀片中心相交于o1点，再以o1为坐标原点建立局部坐标系o
1-x1y1z1，其坐标轴方向与o
t-x
tytzt
方向一致；设标准圆环铣刀的铣刀刀片的刀具母线γ初始位置在x1o1y1平面上，其中心为坐标原点o1，半径r，q为刀具母线γ上的任意一点；在坐标系o
1-x1y1z1中，标准圆环铣刀的截面圆方程为：rq＝[rcosγ
ꢀ‑
rsinγ 0]
t
，其中γ为刀具母线上的点q与o1的连线o1q与x1轴的夹角。
[0012]
优选的是：所述步骤s2具体包括：
[0013]
计算出旋转θ后的刀具母线方程：
[0014][0015]
此时的刀具母线并非为实际加工时的刀刃包络面母线，β为铣刀刀刃所在平面与轴线存在的偏移距离h转换为刀刃平面与轴线的旋转夹角，推导出倾斜刃圆环铣刀的刀刃包络面母线方程为：
[0016][0017]
其中，ω＝arctan(-d3/d1)。
[0018]
优选的是：所述步骤s3具体包括：
[0019]
利用最小二乘法对实际刀刃包络面方程进行数据拟合，得到标准圆的圆心以及半径。每个离散数据点与对应标准圆上的点之间的距离累计之和除以数据点的个数定义为圆环铣刀的误差，得出误差t计算的公式：
[0020][0021]
其中
[0022]
优选的是：所述步骤s4具体包括：
[0023]
根据遗传算法步骤，设置种群规模为20个，染色体个数为3个，进化次数200次，交叉概率设置为0.6，变异概率设置为0.01。对其进行优化，经过200次迭代，优化算法达到收敛，此时误差t最小，得到轴的方向和旋转角度的最优解为：a1＝-8.2409,a2＝-7.2455,c2＝0.0960,θ＝0.1229。
[0024]
另外，基于上述的高速数控鞋楦加工倾斜刃圆环铣刀的设计方法，本发明还提出一种高速数控鞋楦加工倾斜刃圆环铣刀，其特殊之处在于：
[0025]
包括刀体和若干个刀片，所述若干个刀片圆周分布在刀体上；
[0026]
所述刀片为圆台结构，其圆台结构的下底面为刀刃；
[0027]
所述圆台结构的下底面与刀体(1)上优化的轴线之间存在夹角，夹角为7.0417
°
[0028]
进一步地，上述刀片的上底面与刀体固定。
[0029]
进一步地，上述所述刀片的上底面与刀体通过螺钉固定。
[0030]
进一步地，上述刀片的上底面与刀体通过螺钉固定。
[0031]
进一步地，上述刀体的外侧上设有固定座，刀片的上底面通过螺钉固定固定座上。
[0032]
进一步地，上述刀片的数量为三个。
[0033]
相比于现有技术，本发明的有益效果在于：通过本发明一种高速数控鞋楦加工倾斜刃圆环铣刀的优化设计方法，将现有准圆环铣刀的铣刀刀片增加一个绕刀具径向的旋转角，使得其与刀片刃未过刀具回转轴线所产生的误差相抵消，达到了降低误差、提高加工精度的效果，这一改进设计巧妙，结构简单，具有较为广阔的市场前景，可广泛应用于高速数
控鞋楦加工，提高企业效益，便于推广。
附图说明
[0034]
图1为现有准圆环铣刀的侧视图；
[0035]
图2为现有准圆环铣刀的正视图；
[0036]
图3为本发明的侧视图；
[0037]
图4为铣刀刀片的刀刃包络面的三维模型；
[0038]
图5为偏转距离h与旋转角度的关系；
[0039]
图6为适应度曲线；
[0040]
图7为旋转轴的位置；
[0041]
图8为本发明的立体图。
[0042]
图中：1为刀片，2为刀体，3为固定座。
具体实施方式
[0043]
为使本发明实施方式的目的、技术方案和优点更加清楚，下面将结合本发明实施方式中的附图，对本发明实施方式中的技术方案进行清楚、完整地描述，显然，所描述的实施方式是本发明一部分实施方式，而不是全部的实施方式。基于本发明中的实施方式，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施方式，都属于本发明保护的范围。因此，以下对在附图中提供的本发明的实施方式的详细描述并非旨在限制要求保护的本发明的范围，而是仅仅表示本发明的选定实施方式。
[0044]
高速数控鞋楦加工中采用的准圆环铣刀的刀刃平面不过刀具回转轴线，刀具母线为椭圆，而编程时按照标准圆计算，导致存在加工误差。如图1、图2所示，一种高速数控鞋楦加工倾斜刃圆环铣刀，包括刀片1、刀体2和固定座3。高速数控鞋楦加工倾斜刃圆环铣刀刀具直径76mm，所述铣刀刀片1的刀刃直径(圆台结构底面直径)为29mm，三个铣刀刀片呈圆周阵列并均匀固定在刀体2上。虚线所在的铣刀刀片为标准圆环铣刀，而现有准圆环铣刀的铣刀刀刃所在平面未过刀具几何中心，铣刀刀片逆时针偏置了h为5mm，此时的刀具母线为长轴平行于刀具轴向，短轴平行于刀具径向的椭圆，而编程时按照标准圆计算，导致存在加工误差。
[0045]
因此，本发明提出一种高速数控鞋楦加工倾斜刃圆环铣刀及优化设计方法，本方法改进了现有准圆环铣刀由于铣刀刀刃平面安装未过刀具回转轴线导致的加工误差，提高了该刀具的加工精度。如图3所示，将准圆环铣刀的铣刀刀片绕刀具径向旋转一定角度θ，此时的刀具母线是由刀片偏心和旋转叠加形成，近似于标准圆，误差降低。通过计算可以得到两次旋转后铣刀刀片实际刀刃包络面方程，用最小二乘法将其得到的方程的数据点进行拟合，得到倾斜刃圆环铣刀的母线与拟合出的标准圆之间的误差。最后使用matlab进行遗传算法求解出一组让误差达到最小的旋转轴位置和旋转角度。
[0046]
本发明提出一种高速数控鞋楦加工倾斜刃圆环铣刀及优化设计方法，其具体实施步骤如下：
[0047]
步骤1：如图3所示，将准圆环铣刀的铣刀刀片绕刀具径向旋转一定角度θ，此时的刀具母线是由刀片偏心和旋转叠加形成，近似于标准圆，误差降低。建立铣刀刀片的刀刃包
络面的三维模型。设圆环铣刀简化模型的铣刀刀片旋转一周的中心o
t
为坐标原点，以左手法则建立坐标系o
t-x
tytzt
，其中铣刀刀片中心点到o
t
的距离为r，也就是铣刀刀片中心所在的圆的半径。x
totyt
平面与铣刀刀片中心相交于o1点，再以o1为坐标原点建立局部坐标系o
1-x1y1z1，其坐标轴方向与o
t-x
tytzt
方向一致。设标准圆环铣刀的铣刀刀片的刀具母线γ初始位置在x1o1y1平面上，其中心为坐标原点o1，半径r，q为刀具母线γ上的任意一点。在坐标系o
1-x1y1z1中，标准圆环铣刀的截面圆方程为：rq＝[rcosγ
ꢀ‑
rsinγ 0]
t
，其中γ为刀具母线上的点q与o1的连线o1q与x1轴的夹角。
[0048]
步骤2：根据之后计算实际刀刃包络面方程需利用角度来计算这一准则，把铣刀刀刃所在平面与轴线存在的偏移距离h转换为刀刃平面与轴线的旋转夹角β，β为第一次旋转的角度。如图5所示，偏置距离h与旋转角度β之间的关系为：β＝arctan(d/h)，其中d是是准圆环铣刀的回转中心到铣刀刀片中心轴垂直距离，由于d与h已知，可以计算出第一次旋转角度为11.77
°
。
[0049]
已知铣刀刀片第一次旋转角度为β，绕y1的旋转矩阵为：
[0050][0051]
为了减小误差，本发明提出通过将现有准圆环铣刀的铣刀刀片增加一个绕刀具径向的旋转角，使得其与刀片刃未过刀具回转轴线所产生的误差相抵消。在坐标系o
1-x1y1z1下进行第二次旋转且旋转角度为θ而旋转轴为任意轴，绕任意轴旋转θ的步骤如下：
[0052]
1)将旋转轴的一个端点平移至原点；
[0053]
2)将旋转轴旋转至yoz平面；
[0054]
3)将旋转轴旋转至于z轴重合；
[0055]
4)绕z轴旋转θ度；
[0056]
5)执行步骤3的逆过程；
[0057]
6)执行步骤2的逆过程；
[0058]
7)执行步骤1的逆过程。
[0059]
通过上述计算即可得到绕任意轴旋转的旋转矩阵m，由于计算过程复杂现直接列出绕任意轴的旋转矩阵m：
[0060][0061]
m1＝u2+(v2+w2)cosθ
[0062]
m2＝uv(1-cosθ)+wsinθ
[0063]
m3＝uw(1-cosθ)-vsinθ
[0064]
m4＝uv(1-cosθ)-wsinθ
[0065]
m5＝v2+(u2+w2)
×
cosθ
[0066]
m6＝vw(1-cosθ)+usinθ
[0067]
m7＝uw(1-cosθ)+vsinθ
[0068]
m8＝vw(1-cosθ)-usinθ
[0069]
m9＝w2+(v2+u2)
×
cosθ
[0070]m10
＝[a(v2+w2)]-[u(bv+cw)]
×
(1-cosθ)+(bw-cv)
×
sinθ
[0071]m11
＝[b(u2+w2)]-[v(au+cw)]
×
(1-cosθ)+(cu-aw)
×
sinθ
[0072]m12
＝[c(u2+v2)]-[w(bv+au)]
×
(1-cosθ)+(av-cv)bu
×
sinθ
[0073]
其中，(u,v,w)＝(a2,b2,c2)-(a1,b1,c1)，且为单位向量，(a2,b2,c2)，(a1,b1,c1)为旋转轴的两个端点。m1代替旋转矩阵中第一行第一列的数据、m2代替第二行第一列，以此类推，即可用旋转矩阵m求出在坐标系o
1-x1y1z1计算出旋转θ后的刀具母线方程：rq'＝m
×my
×rq1
，计算结果如下：
[0074][0075]
此时的刀具母线并非为实际加工时的刀刃包络面母线，在坐标系o
t-x
tytzt
下，圆环铣刀实际刀刃包络面方程为：
[0076][0077]
计算出：
[0078][0079]
其中：
[0080]
d1＝rcosγ
·
cosβ
·m1-rsinγ
·
m4+rcosγ
·
sinβ
·
m7+m
10
+r
[0081]
d2＝rcosγ
·
cosβ
·m2-rsinγ
·
m5+rcosγ
·
sinβ
·
m8+m
11
[0082]
d3＝rcosγ
·
cosβ
·m3-rsinγ
·
m6+rcosγ
·
sinβ
·
m9+m
12
[0083]
ω为刀具母线在坐标系o
t-x
tytzt
中绕着z
t
旋转的角度，ω∈[0,2π]。
[0084]
为求得实际刀刃包络面在x1o1y1平面上的刀具母线k，令d1sinω+d3cosω＝0，求出此时ω＝arctan(-d3/d1)。计算出在坐标系o
1-x1y1z1中的刀具母线k上任一点p的表达式为：
[0085][0086]
步骤3：计算倾斜刃圆环铣刀的母线与拟合出的标准圆之间的误差。
[0087]
通过步骤2计算出的r
p
可以得到xi＝d1cosα-d3sinα、yi＝d2、i∈(1,2,3...n)的样本集，样本集的数据点个数与γ的个数一致，用最小二乘法拟合这些离散数据点，定义每个离散数据点与对应标准圆上的点之间的距离累计之和除以数据点的个数为圆环铣刀的误差。同时拟合得到的标准圆的半径为旋转了两次的圆环铣刀的有效加工圆半径，用最小二
乘法拟合圆。
[0088]
设标准圆的方程为：r2＝(x-a)2+(y-b)2[0089]
样本集xi、yi到圆边缘的距离平方与半径平方的差为：
[0090]
δi＝(x
i-a)2+(y
i-b)
2-r2[0091]
令q(a,b,c)为δi平方和：
[0092]
q(a,b,c)＝∑δ
i2
＝∑(x
i2
+y
i2
+axi+byi+c)2[0093]
其中a＝-2a、b＝-2b、c＝a2+b
2-r2，求参数a，b，c就是求其偏导,令偏导等于0：
[0094][0095][0096][0097]
解出：
[0098]
其中：c＝n∑x
i2-∑xi∑xi、d＝n∑xiy
i-∑xi∑yi、
[0099]
e＝n∑x
i3
+n∑xiy
i2-∑(x
i2
+y
i2
)∑xi、g＝n∑y
i2-∑yi∑yi、
[0100]
h＝n∑y
i3
+n∑x
i2yi-∑(x
i2
+y
i2
)∑yi。
[0101]
求出来拟合出来的标准圆的圆心坐标为半径为
[0102]
标准圆参数方程为：得出误差t计算的公式：
[0103][0104]
误差t的大小与旋转轴的位置(a1,b1,c1)、(a2,b2,c2)以及旋转角度θ有关，对现在加工常用的准圆环铣刀进行误差计算得到其误差为0.0639。
[0105]
步骤4：进行遗传算法，设置种群规模为20个，染色体个数为3个，进化次数200次，交叉概率设置为0.6，变异概率设置为0.01，设计变量二进制长度。设置遗传代数计数器gen初始值为0。接着设置计算种群中的个体适应度，适应度越小的染色体越健壮，下一代生成概率越大。
[0106]
在上述的过程中把旋转轴(u,v,w)＝(a2,b2,c2)-(a1,b1,c1)以及旋转角度θ当作变量，为了让准圆环铣刀的铣刀刀片经过二次旋转后的刀具母线关于x轴对称，设定旋转轴位于x1z1平面内，限定b1,b2为零，且设定旋转轴中一点只在x轴上变化，另外一个点满足：(a
2-a1)2+c
22
＝1
[0107][0108]
根据遗传算法步骤，对其进行优化，经过200次迭代，优化算法达到收敛，此时误差t最小，适应度变化曲线如图5所示。从图中可以看出，经过10代以后，历史最佳适应度曲线趋于平稳，按初始设定的最大迭代次数200次，可以认为此时优化出的旋转轴位置以及旋转度数对应的加工误差为最低。此时的参数为：a1＝-8.2409,a2＝-7.2455,c2＝0.0960,θ＝0.1229，如图7所示，根据优化的旋转轴位置为a1b1，最小误差为0.02297，比准圆环铣刀的误差降低了64.33％。
[0109]
参见图3、图5和图7，基于上述的高速数控鞋楦加工倾斜刃圆环铣刀的设计方法，本发明还提出一种高速数控鞋楦加工倾斜刃圆环铣刀，包括刀体1和若干个刀片2，所述若干个刀片2圆周分布在刀体1上；所述刀片2为圆台结构，其圆台结构的下底面为刀刃；所述圆台结构的下底面与上述优化得到的a1b1轴线之间存在夹角，所述圆台结构的下底面与刀体1的轴线之间的夹角为7.0417
°
。
[0110]
作为本发明的一个优选实施例，所述刀片2的上底面与刀体1固定。
[0111]
作为本发明的一个优选实施例所述所述刀片2的上底面与刀体1通过螺钉固定。
[0112]
作为本发明的一个优选实施例，所述刀体1的外侧上设有固定座3，刀片2的上底面通过螺钉固定固定座3上。
[0113]
优选地，所述刀片2的数量为三个，所述三个刀片2在刀体1周围圆周均布。
[0114]
本发明通过将现有准圆环铣刀的铣刀刀片增加一个绕刀具径向的旋转角，使得其与刀片刃未过刀具回转轴线所产生的误差相抵消，达到了降低误差、提高加工精度的效果。
[0115]
以上所述仅为本发明的实施例，并非以此限制本发明的保护范围，凡是利用本发明说明书及附图内容所作的等效结构或等效流程变换，或直接或间接运用在其他相关的系统领域，均同理包括在本发明的保护范围内。