一种考虑五轴机床定位误差的在机测量误差预测方法

1.本发明属于机械精密制造与测量领域，具体涉及一种考虑五轴机床定位误差的在机测量误差预测方法。


背景技术：

2.在机测量是通过在数控机床主轴上加装测头，将承担加工任务的机床转化为在机测量的载体，是实现加工工序中对工件在机测量的工艺方法。相较于目前生产车间常见的三坐标测量，在机测量能够避免工件的重复装夹，保证测量过程与加工过程的连续性，是实现自适应加工的关键技术，在生产一线具有广阔的应用前景。然而，机床作为机内测量的载体，测量过程中机床因各机构运动会引入诸多误差，这些直接影响机床精度，进而导致在机测量精度的可信度一直受到质疑。
3.需要明确强调的是，定位误差是影响机床精度的主要因素，在机床出厂和定期运维检测中，定位精度是衡量机床整体工作性能的重要指标。目前，iso标准中给出了辨识定位误差的相关设备和方法，许多学者也针对定位误差的辨识和补偿进行了研究。然而，少有学者深入研究在机测量过程中机床定位误差的积累方式，缺乏依据定位误差分布来进行在机测量误差与优化测量工艺的预测。此外，由于五轴机床具有较高的灵活性，工件上同一待测点往往可在机床内的不同位置实现测量，而不同位置测量引入的定位误差又存在差异。当前在机测量规划中通常依靠软件自动选取某一可行的测量位置进行测量，缺乏对机床引入定位误差影响程度的分析，导致在机测量精度受到定位误差分布的影响，从而在机测量结果存在不确定性。
4.因此，研发一种分析五轴机床定位误差分布来预测在机测量误差的方法具有十分重要的意义。


技术实现要素：

5.为了解决上述技术问题，提高在机测量检测精度，提出一种考虑五轴机床定位误差的在机测量误差预测方法，将机床内中可行的测量位置转化机床旋转轴角度组合，在由旋转轴角度组合构成的二维平面中构建测量可行区域，建立定位误差对在机测量误差的影响模型，并基于该模型预测该区域内的测量误差分布，能够用于选取定位误差影响最小的测量位置。该方法能够有效、精确地分析五轴机床的在机测量误差分布，进而提高在机测量的精度和可信度。
6.本发明解决其技术问题所采用的技术方案：一种考虑五轴机床定位误差的在机测量误差预测方法，其特征在于：包括以下步骤：
7.步骤1：识别五轴机床定位误差，并拟合定位误差分布；
8.步骤2：不同的五轴机床旋转轴转角组合下，待测点的位置和外法矢方向在机床坐标系csm内均不同，使得待测点的测量路径不唯一。由于机床结构的限制，b、c旋转轴的转角范围分别为[b
min
,b
max
]和[c
min
,c
max
]。对于一个给定的旋转轴角度组合，待测点的位置和外
法矢方向在机床坐标系csm内唯一确定，在指定探测距离后，待测点的测量路径唯一确定。因此，将可行的测量路径转化为五轴机床两旋转轴角度点集，构成待测点的测量可行域。
[0009]
具体计算两类测量路径约束条件下待测点q的测量可行域，包括：
[0010]
测量路径约束条件一：保证探针红宝石球赤道以下区域触碰待测点q，即时的测量可行域，这里是在探针坐标系csr下待测点q外法矢nr的z方向分量；
[0011]
测量路径约束条件二：保证测量路径在机床运动行程内，探针定位点理论位置pm和待测点理论位置qm同时位于探针可达区域θ内，即qm∈θ且pm∈θ时的测量可行域；
[0012]
步骤3：在机床坐标系csm下，建立待测点q的最终测量结果与理论位置qm间的在机测量误差预测模型err；
[0013]
步骤4：结合步骤1获得的定位误差分布和步骤2获得待测点q的测量可行域，计算测量可行域内两旋转轴b、c的每一个角度组合(b,c)对应的定位误差，并将定位误差与角度组合代入步骤3建立的测量误差预测模型err中，预测测量可行域内两旋转轴b、c的所有角度组合(b,c)对应的测量误差分布。
[0014]
进一步的，在步骤1中，识别五轴机床的定位误差及其拟合定位误差分布的具体过程为：
[0015]
步骤1.1：在机床内使用激光干涉仪，通过改变分光镜、反射镜、干涉仪的位置识别x、y、z三个线性轴的离散位置定位误差σ
x-y-z
＝[σ
x
,σy,σz]
′
，通过加装回转轴校准装置识别b、c两个旋转轴角度定位误差σ
b-c
＝[σb,σc]
′
；
[0016]
步骤1.2：基于步骤1.1识别的离散位置与角度的定位误差量，使用样条曲线拟合x、y、z、b轴的定位误差测量结果，使用样条曲面拟合c轴的定位误差测量结果，形成各轴行程范围内的定位误差分布。
[0017]
进一步的，在步骤2中，计算时的测量可行域的过程为：
[0018]
步骤2.1-1：在探针红宝石球心点建立探针坐标系csr后，基于机床结构，
[0019]
在探针红宝石球心点建立探针坐标系csr，基于机床结构建立从工件坐标系csw到探针坐标系csr的变换矩阵r为：
[0020][0021]
式中，斜体b、c为b、c旋转轴的角度；
[0022]
步骤2.1-2：设探针坐标系csr下待测点q外法矢工件坐标系csw下待测点q外法矢和b、c旋转轴的角度组合为(b,c)，由变换矩阵r构造三者间的关系，可用数学模型表示为：
[0023][0024]
步骤2.1-3：对于某一待测点，测量路径可行域的条件之一为保证探针红宝石球赤
道以下区域触碰待测点。在机测量中要求探针沿待测点外法矢的反向触碰待测点。在b、c旋转轴角度组合(b,c)已知的条件下，在探针坐标系csr下的外法矢方向确定，由此获得探针红宝石球上的触碰位置，即通过探针红宝石球赤道以下区域触碰待测点的条件来表示测量可行域，进一步表示为：
[0025][0026]
式中[b
min
,b
max
]与[c
min
,c
max
]分别为b、c旋转轴的转角范围。
[0027]
进一步的，在步骤2中，计算qm∈θ且pm∈θ时的测量可行域的过程为：
[0028]
步骤2.2-1：基于机床结构，建立从工件坐标系csw到机床坐标系csm的变换矩阵m：
[0029][0030]
式中，斜体b、c为b、c旋转轴的角度，[δx
p
,δy
p
,δz
p
]为主轴点在机床坐标系csm中的坐标，[δxw,δyw,δzw]为工件坐标系csw原点在机床坐标系csm中的坐标；
[0031]
步骤2.2-2：对于某一待测点，测量路径可行域的条件之一为保证测量路径在机床运动行程内。机内测量过程中，探针需要先移动到定位点，在沿着待测点外法矢方向的反向运动，直至测头触发。将定位点到待测点的距离称为探测距离l。计算探针定位点在工件坐标系csw中的位置pw：
[0032]
pw＝qw+l
·nw
，
[0033]
式中qw为待测点q在工件坐标系csw下的理论位置。
[0034]
步骤2.2-3：设待测点q分别在机床坐标系下csm的理论位置在工件坐标系csw中的位置由变换矩阵m构造二者间的关系，可用数学模型表示为：
[0035][0036]
步骤2.2-4：设探针定位点分别在机床坐标系csm下的理论位置在工件坐标系csw中的位置由变换矩阵m构造二者间的关系，可用数学模型表示为：
[0037][0038]
步骤2.2-5：将机床主轴运动空间中探针在空间中可到达的区域称为探针可达区域，记为θ。在机床坐标系csm下，探针定位点理论位置pm和待测点理论位置qm同时位于探针可达区域θ内时，可保证测量路径在机床运动行程内，即qm∈θ且pm∈θ来表示测量可行域。结合步骤2.3-2和步骤2.3-3，qm∈θ且pm∈θ进一步表示为：
[0039][0040]
式中[x
min
,x
max
]，[y
min
,y
max
]，[z
min
,z
max
]分别为机床x、y、z三个线性轴的行程范围。
[0041]
进一步的，步骤3中建立待测点q的最终测量结果与理论位置qm间的在机测量误差预测模型err的具体过程为：
[0042]
步骤3.1：将工件外表面看作一系列微小平面的组合，用待测点q表示微小平面的中心点，用待测点q的外法矢表示微小平面的平面法矢；
[0043]
步骤3.2：工件装夹找正后，无定位误差影响的条件下，由变换矩阵m和待测点q在工件坐标系csw下的外法矢方向nw建立待测点q机床坐标系csm下的理论外法矢nm为：
[0044][0045]
计算探测定位点在机床坐标系csm下的理论位置pm，pm＝qm+l
·
nm，式中l同上；进一步计算探针触碰到工件时探针红宝石球球心点理论位置hm，hm＝q
m-r
·
nm，式中r探针红宝石球的半径；
[0046]
步骤3.3：工件装夹找正后，存在定位误差的条件下，结合步骤1.1中识别的x、y、z三个线性轴的离散位置定位误差σ
x-y-z
＝[σ
x
,σy,σz]
′
与b、c两个旋转轴角度定位误差σ
b-c
＝[σb,σc]
′
，计算在机床坐标系csm下探测定位点的实际位置为：
[0047][0048]
计算待测点q在机床坐标系csm下的实际位置为：
[0049][0050]
进一步计算待测点q在机床坐标系csm下的实际外法矢为：
[0051][0052]
步骤3.4：在测量时，探针将从探针定位点的实际位置出发向待测点理论位置qm接近，计算在机床坐标系csm中的实际探针接近方向d为：
[0053][0054]
步骤3.5：结合步骤3.3和步骤3.4，探针触碰到工件表面使测头触发时的探针红宝石球心的实际位置为：
[0055][0056]
在考虑x、y、z三个线性轴定位误差影响条件下，探针红宝石球心的记录位置为：
[0057][0058]
式中hσ
x-y-z
＝[hσ
x
，hσy，hσz]
′
为处的线性轴定位误差。
[0059]
步骤3.6：在考虑步骤3.5计算的探针红宝石球心的记录位置的基础上，待测点q在机床坐标系csm下的最终测量结果为：
[0060][0061]
步骤3.7：在机床坐标系csm下，计算待测点q的最终测量结果与待测点理论位置qm间的距离绝对误差作为在机测量误差的预测模型。结合步骤3.5和步骤3.6的结果，进一步err可表示为：
[0062][0063]
有益效果
[0064]
本发明的有益效果在于：
[0065]
1、将待测点的可行测量位置转化为可行的旋转轴角度组合，把测量路径优化问题转变为二维平面点集的规划问题；
[0066]
2、建立针对单一待测点测量路径可行的条件，给出了待测点位置及其外法矢方向对机床旋转轴角度组合的约束；
[0067]
3、以在检测中减少机床定位误差影响、提高在机测量精度为目的，进行在机测量误差预测与测量路径的优化，能够降低在机测量误差，提升测量结果的可信程度；
[0068]
4、该方法稳定性好，可推广应用于其他多轴机床的在机测量，具有一定的工程应用价值。
[0069]
本发明的附加方面和优点将在下面的描述中部分给出，部分将从下面的描述中变得明显，或通过本发明的实践了解到。
附图说明
[0070]
本发明的上述和/或附加的方面和优点从结合下面附图对实施例的描述中将变得明显和容易理解，其中：
[0071]
图1五轴机床各轴定位误差分布；
[0072]
图2测量可行图；
[0073]
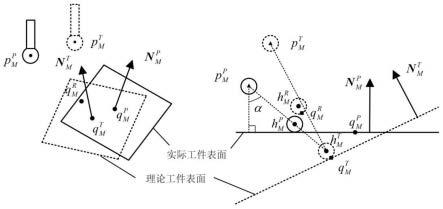
图3定位误差对在机测量的影响；
[0074]
图4定位误差影响下的在机测量过程；
[0075]
图5在机测量误差分布预测图；
[0076]
图6标准块上待测点分布；
[0077]
图7(a)实施例1中待测点1的实验测量误差与预测结果对比；(b)实施例1中待测点2的实验测量误差与预测结果对比；(c)实施例1中待测点3的实验测量误差与预测结果对比
具体实施方式
[0078]
下面详细描述本发明的实施例，所述实施例的示例在附图中示出，其中自始至终相同或类似的标号表示相同或类似的元件或具有相同或类似功能的元件。下面通过参考附图描述的实施例是示例性的，旨在用于解释本发明，而不能理解为对本发明的限制。
[0079]
步骤1：为了分析定位误差对测量误差的影响，需要识别五轴机床各轴的定位误差。使用激光干涉仪，通过改变分光镜、反射镜、干涉仪的位置测量线性轴定位误差，通过加装回转轴校准装置测量旋转轴定位误差。基于测量得到离散位置与角度的定位误差，使用样条曲线拟合x、y、z、b轴的定位误差测量结果，使用样条曲面拟合c轴的定位误差测量结果，获得各轴行程范围内的定位误差分布，如图1所示。
[0080]
步骤2：计算测量可行域。
[0081]
上述步骤2的具体实现方法为：
[0082]
步骤2.1：不同的五轴机床旋转轴转角组合下，待测点的位置和外法矢方向在机床坐标系内均不同，使得待测点的测量路径不唯一。对于一个给定的旋转轴角度组合，待测点的位置和外法矢方向在机床坐标系内唯一确定，因此在指定探测距离后，待测点的测量路径唯一确定。故可将可行的测量位置转化为五轴机床两旋转轴角度点集，构成该待测点的测量可行域。在探针红宝石球心点建立探针坐标系csr，基于机床结构建立从工件坐标系到探针坐标系的变换矩阵r为：
[0083][0084]
由变换矩阵r建立探针坐标系下待测点外法矢工件坐标系下待测点外法矢与旋转角度(b,c)的关系如下：
[0085][0086]
为满足保证探针红宝石球赤道以下区域触碰待测点的条件，令获得公式(3)所示的测量可行域的旋转轴角度约束条件一。
[0087][0088]
式中[b
min
,b
max
]与[c
min
,c
max
]分别为b、c旋转轴的转角范围。
[0089]
步骤2.2：基于机床结构，建立从工件坐标系csw到机床坐标系csm的变换矩阵m为：
[0090]
[0091]
式中[δx
p
,δy
p
,δz
p
]为主轴点在机床坐标系csm中的坐标，[δxw,δyw,δzw]为工件坐标系csw原点在机床坐标系csm中的坐标。
[0092]
机内测量过程中，探针需要先移动到定位点，再沿着待测点外法矢方向的反向运动，直至测头触发。将探针定位点到待测点的距离称为探测距离l。计算探针定位点在工件坐标系csw中的位置pw：
[0093]
pw＝qw+l
·nw
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(5)
[0094]
其中qw为待测点在工件坐标系下的位置。
[0095]
进而在机床坐标系csm下计算待测点q的理论位置qm，令其坐标为则：
[0096][0097]
同理，在机床坐标系csm下计算探针定位点理论位置pm，令其坐标为则：
[0098][0099]
步骤2.3：将机床主轴运动空间中探针在空间中可到达的区域称为探针可达区域，记为θ，该区域在机床坐标系csm内为一立方体。机床三个线性轴的行程范围分别为[x
min
,x
max
]，[y
min
,y
max
]，[z
min
,z
max
]。当qm∈θ且pm∈θ时，即可保证测量路径在机床运动行程内。获得公式(8)所示的测量可行域的旋转轴角度约束条件二。
[0100][0101]
式中b∈[b
min
,b
max
],c∈[c
min
,c
max
]。同时满足两个约束条件的五轴机床两旋转轴角度点集即为测量可行图，如图2所示。
[0102]
步骤3：在机床坐标系csm下，建立待测点q的最终测量结果与理论位置qm间的在机测量误差预测模型err。
[0103]
上述步骤3的具体实现方法为：
[0104]
步骤3.1：基于微分思想，将工件外表面看作一系列微小平面的组合，用待测点q表示微小平面的中心点，用待测点q的外法矢nw表示微小平面的平面法矢；
[0105]
步骤3.2：工件装夹找正后，无定位误差影响的条件下，由变换矩阵m和待测点q在工件坐标系csw下的外法矢方向nw建立待测点q机床坐标系csm下的理论外法矢nm为：
[0106][0107]
进一步，计算探测定位点在机床坐标系csm下的理论位置pm：
[0108]
pm＝qm+l
·
nmꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(10)
[0109]
进一步，计算探针触碰到工件时探针红宝石球球心点理论位置hm：
[0110]hm
＝q
m-r
·
nmꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(11)
[0111]
其中r为探针红宝石球半径。
[0112]
步骤3.3：工件装夹找正后，存在定位误差的条件下，即考虑x、y、z三个线性轴的离散位置定位误差σ
x-y-z
＝[σ
x
,σy,σz]
′
与b、c两个旋转轴角度定位误差σ
b-c
＝[σb,σc]
′
的影响时，在机床坐标系csm下探测定位点的实际位置为：
[0113][0114]
另外，由于机床在运动时存在角度定位误差(σb,σc),转台的实际测量角度将改变为(b+σb,c+σc)，工件坐标系csw在机床坐标系csm中的位置将发生变化，将理论测量角度组合下的辅助坐标系csw称为理论辅助坐标系将此时的工件坐标系csw称为实际工件坐标系定位误差的影响如图3所示。
[0115]
进一步，待测点q在机床坐标系csm下的实际位置为：
[0116][0117]
进一步，待测点q在机床坐标系csm下的实际外法矢为：
[0118][0119]
步骤3.4：由于定位误差无法被数控系统识别，故在进行测量时，探针将从探针定位点的实际位置出发向理论测量点qm接近，如图4所示，则则在机床坐标系csm中的实际探针接近方向d为：
[0120][0121]
进一步，探针触碰到工件表面使测头触发时的探针红宝石球心的实际位置
[0122][0123]
在考虑x、y、z三个线性轴定位误差影响条件下，探针红宝石球心的记录位置为：
[0124][0125]
其中hσ
x-y-z
＝[hσ
x
，hσy，hσz]
′
为处的线性轴定位误差。
[0126]
步骤3.5：由于半径补偿方向仍为待测点外法矢理论方向的反向，所以在考虑步骤
4.4计算的探针红宝石球心的记录位置的基础上，待测点q在机床坐标系csm下的最终测量结果为：
[0127][0128]
步骤3.6：结合步骤3.4和步骤3.5的结果，在机床坐标系csm下，计算待测点q的最终测量结果与待测点理论位置qm间的距离绝对误差，即作为在机测量误差的预测模型err：
[0129][0130]
步骤4：步骤1获得的定位误差分布能够得到任意位置与转台旋转角度下机床各轴的定位误差。通过步骤2可以获得待测点的测量可行域，可行域内每个角度组合即对应一个转台旋转角度组合下机床内待测点的位置，基于定位误差的分布可以得到可行域内任意角度组合对应的各轴定位误差，将定位误差与角度组合代入步骤3提出的测量误差预测模型，即可预测可行域内任一角度组合对应的测量误差。对可行域内所有角度组合的定位误差进行预测，即可得到在机测量误差分布预测图，如图5所示。
[0131]
下面以标准块上3个测量点的在机测量为实施例进行说明：
[0132]
本发明中在机测量系统为北京精雕jd50系统，所采用的测头是renishaw公司的omp40触发式测头，使用的标准块尺寸为35
×8×
70mm。
[0133]
实施例1：标准块上共分布3个待测点，如图6所示，对应的坐标如表1所示。
[0134]
表1待测点的三坐标测量机检测结果
[0135][0136]
依据机床各轴行程范围及定位误差分布，采用本技术中的在机测量误差预测模型分别得到三个待测点的测量误差分布。在b轴采样角度为b＝-15
°
,-30
°
,-45
°
,-60
°
,-75
°
,-90
°
，c轴采样角度为c＝0
°
,30
°
,60
°
,90
°
,120
°
,150
°
,180
°
,210
°
,240
°
,270
°
,300
°
,330
°
，共72个采样角度组合。根据三个待测点的测量误差分布，获得测量可行域内的采样角度测量误差预测量。在相同采样角度下分别对三个待测点进行测量，测量重复三次，得到的三个待测点的测量误差实测结果。三个待测点的测量误差预测结果和实测结果分别如表2～4所示。
[0137]
表2待测点1测量误差预测结果与实测结果
[0138]
[0139][0140]
表3待测点2测量误差预测结果与实测结果
[0141][0142][0143]
表4待测点3测量误差预测结果与实测结果
[0144]
[0145][0146]
实施例1中待测点1～3的实验测量误差于预测结果对比如图7(a)～7(c)所示，可以看出，采用本技术中在机测量误差预测方法可以较好的预测测量误差分布，预测误差在0.01mm以下，证明了该方法的实用性和有效性。