三维造型方法与流程

本发明涉及三维形状造型物的制造方法，该制造方法的特征是在反复进行粉末层的形成工序以及对该粉末层的利用激光束或电子束实现的烧结工序的情况下，能够选择各层叠单位的厚度。

背景技术：

在三维造型方法中，各层叠单位的厚度大致情况是恒定的。

实际上，在专利文献1中，考虑三维造型涉及的最表面层的厚度的适当化也并不是使该厚度相应于各层叠单位而变化。

但是，在专利文献2中公开了下述内容：在进行规定的阶段中的层叠时，在检测到超过层叠厚度的凸部的情况下，对于下一阶段中的层叠的厚度进行设定以使得其超过上述凸部的高度。

但是，并不是设定这样的厚度并且基于与造型对象物的整体形状对应的统一的基准来选择厚度。

在实际的三维造型中，造型对象物的水平方向、即与进行层叠的高度方向垂直的方向上的截面形状的变化与各层叠单位的厚度存在密切的关系。

具体地说明，在各层叠截面的形状沿高度方向较大地变化的情况下，通过使各层叠单位的厚度较小，能够准确地实现造型对象物的本来的形状，相反地，在沿上下方向的厚度的变化缓慢的情况下，即使将各层叠单位的厚度设定得较大，造型对象物的本来的形状也并不会反映得不准确。

然而，在现有技术中，完全没有考虑与水平方向截面的沿上下方向的变化状况对应地适当设定各层叠单位的厚度。

在先技术文献

专利文献

专利文献1：日本特开2013-67036号公报

专利文献2：日本特开2015-112752号公报

技术实现要素：

本发明的课题是提供一种三维造型方法，其中，按照造型对象物的水平方向截面沿高度方向变化的程度，来适当地设定各层叠单位的厚度。

为解决所述课题，本发明的基本构成包括以下技术方案。

(1)一种三维造型方法，是通过粉末层形成工序和烧结工序的交替反复进行来在容器内进行层叠的三维造型方法，所述烧结工序是通过移动的激光束或电子束的照射来对所述粉末层进行烧结的工序，

沿高度方向将层叠区域设定为多个等幅区分区域后，通过以下步骤，选择各等幅区分区域中的层叠数n，从而选择各等幅区分区域中的各层叠单位的厚度，

步骤1：采用直角坐标即(x，y)坐标，对于预先设定好了造型的模型的等幅区分区域中的形成上下两侧的边界的各截面，由记录于cam或控制用计算机中的形成各截面的外周的坐标(x1，y1)、…、(xi，yi)、…、(xh，yh)，通过

x0＝(x1+…+xi+…+xh)/h

y0＝(y1+…+yi+…+yh)/h

的运算来算出该各截面的中心位置(x0，y0)，并且，对于从该中心位置(x0，y0)到外侧周围上的各坐标(x1，y1)、…、(xi，yi)、…、(xh，yh)的平均距离r，在进行

的计算和记录后，通过

r＝(r1+…+ri+…+rh)/h

的运算来算出，

并且，对于各等幅区分区域，算出上侧的边界上的各截面的所述平均距离与下侧的边界上的各截面的所述平均距离之差的绝对值d；

步骤2：设定设想d为0的情况下的最小层叠数n1，检测d的最大值d，并且，设定形成有最大值d的等幅区分区域中的最大层叠数n2；

步骤3：在最小值n1与最大值n2之间随着d变大而设定大的数值n，通过n＝[n]来选择层叠数n，其中，[]是高斯符号，表示整数的单位；

步骤4：对于上述步骤1中的各等幅区分区域，设定通过上述步骤3中的层叠数n个来沿上下方向进行了进一步的等幅区分的情况下的各n个截面的与上述步骤1中的模型切合(相符)的外侧周围坐标；和

步骤5：在实际的造型时，在各等幅区分区域中，基于通过上述步骤3所选择的层叠数n进行粉末层的形成以及烧结，并且对切削工具的移动进行控制以使通过上述步骤4所设定的外侧周围坐标的位置成为最终的切削位置。

(2)一种三维造型方法，是通过粉末层形成工序和烧结工序的交替反复进行来在容器内进行层叠的三维造型方法，所述烧结工序是通过移动的激光束或电子束的照射来对所述粉末层进行烧结的工序，

沿高度方向将层叠区域设定为多个等幅区分区域后，通过以下步骤，选择各等幅区分区域中的层叠数n，从而选择各等幅区分区域中的各层叠单位的厚度，

步骤1：采用直角坐标即(x，y)坐标，对于预先设定好了造型的模型的等幅区分区域中的形成上下两侧的边界的各截面，通过cam或控制用计算机来算出该各截面的最大横向幅度与最大纵向幅度的总和，并且，对于各等幅区分区域，算出上侧的边界上的各截面的所述总和与下侧的边界上的各截面的所述总和之差的绝对值d；

步骤2：设定设想d为0的情况下的最小层叠数n1，检测d的最大值d，并且，设定形成有最大值d的等幅区分区域中的最大层叠数n2；

步骤3：在最小值n1与最大值n2之间随着d变大而设定大的数值n，通过n＝[n]来选择层叠数n，其中，[]是高斯符号，表示整数的单位；

步骤4：对于所述步骤1中的各等幅区分区域，设定通过所述步骤3中的层叠数n个来沿上下方向进行了进一步的等幅区分的情况下的各n个截面的与所述步骤1中的模型切合的外侧周围坐标；

步骤5：在实际的造型时，在各等幅区分区域中，基于通过所述步骤3所选择的层叠数n进行粉末层的形成以及烧结，并且对切削工具的移动进行控制以使通过所述步骤4所设定的外侧周围坐标的位置成为最终的切削位置。

(3)一种三维造型方法，是通过粉末层形成工序和烧结工序的交替反复进行来在容器内进行层叠的三维造型方法，所述烧结工序是通过移动的激光束或电子束的照射来对所述粉末层进行烧结的工序，

沿高度方向将层叠区域设定为多个等幅区分区域后，通过以下步骤，选择各等幅区分区域中的层叠数n，从而选择各等幅区分区域中的各层叠单位的厚度，

步骤1：采用旋转坐标即(r，θ)坐标，对于预先设定好了造型的模型的等幅区分区域中的形成上下两侧的边界的各截面，由记录于cam或控制用计算机中的外侧周围的坐标(r1，θ1)、…、(ri，θi)、…、(rh，θh)，通过

r0＝(r1+…+ri+…+rh)/h

θ0＝(θ1+…+θi+…+θh)/h

的运算来算出该各截面的中心位置(r0，θ0)，并且，关于从该中心位置(r0，θ0)到形成外侧周围的各坐标(r1，θ1)、…、(ri，θi)、…、(rh，θh)的距离，使已设定的(r，θ)坐标的原点(0,0)向上述(r0，θ0)的位置位移，并且，计算基于该位移而获得的新的中心位置(0,0)与各外侧周边的坐标位置之间的距离r1’、…、ri’、…、rh’，从基于该计算而获得的距离中选择最大距离，

并且，对于各等幅区分区域，算出上侧的边界上的各截面的所述最大距离与下侧的边界上的各截面的所述最大距离之差的绝对值d；

步骤2：设定设想d为0的情况下的最小层叠数n1，检测d的最大值d，并且，设定形成有最大值d的等幅区分区域中的最大层叠数n2；

步骤3：在最小值n1与最大值n2之间随着d变大而设定大的数值n，通过n＝[n]来选择层叠数n，其中，[]是高斯符号，表示整数的单位；

步骤4：对于所述步骤1中的各等幅区分区域，设定通过所述步骤3中的层叠数n个来沿上下方向进行了进一步的等幅区分的情况下的各n个截面的与所述步骤1的模型切合的外侧周围坐标；

步骤5：在实际的造型时，在各等幅区分区域中，基于通过所述步骤3所选择的层叠数n进行粉末层的形成以及烧结，并且对切削工具的移动进行控制以使通过所述步骤4所设定的外侧周围坐标的位置成为最终的切削位置。

在立足于基本构成(1)、(2)、(3)的本发明中，对应于在水平方向上的各等幅区分区域的边界上的截面形状的变化，即，在基本构成(1)的情况下，对应于距中心的平均距离的变化，在基本构成(2)的情况下，对应于直角坐标中的横向以及纵向的最大幅度的总和的变化，在基本构成(3)的情况下，对应于旋转坐标中的距中心位置的最大距离的变化，来设定各等幅区分区域中的层叠数(n)，从而对应于各层叠单位中的水平方向面的变化来设定适当的厚度以及基于该层叠数(n)的各截面的周围的坐标，由此能够实现准确的造型对象物的形状。

附图说明

图1(a)是在基本构成(1)中，计算中心位置、以及从中心位置到外侧周围的平均距离以及上下的边界截面中的所述平均距离之差的绝对值d的情况下的成为该计算的对象的各等幅区分区域的边界上的截面图。

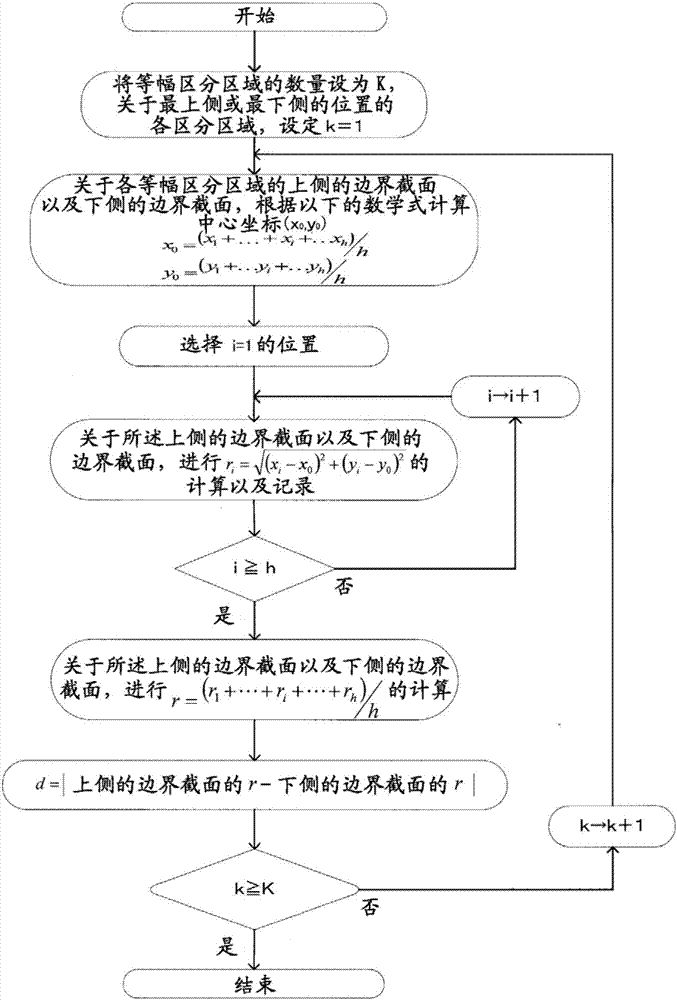
图1(b)是表示在基本构成(1)中，计算中心位置、以及从中心位置到外侧周围的平均距离以及上下的边界截面中的所述平均距离之差的绝对值d的情况下的该计算的顺序的流程图。

图2(a)是在基本构成(2)中，计算最大横向幅度与最大纵向幅度的总和以及上下的边界截面中的所述总和之差的绝对值d的情况下的成为该计算的对象的各等幅区分区域的边界上的截面图。

图2(b)是表示在基本构成(2)中，计算最大横向幅度与最大纵向幅度的总和以及上下的边界截面中的所述总和之差的绝对值d的情况下的该计算的顺序的流程图。

图3(a)是在基本构成(3)中，计算中心位置、以及距中心位置的最大距离以及上下的边界截面中的所述最大距离之差的绝对值d的情况下的成为该计算的对象的各等幅区分区域的边界上的截面图。

图3(b)是表示在基本构成(3)中，计算中心位置、以及距中心位置的最大距离以及上下的边界截面中的所述最大距离之差的绝对值d的情况下的该计算的顺序的流程图。

图4是表示在预先设定好了造型的模型中设定了等幅区分区域的状态的截面图。

图5表示用于在基本构成(1)、(2)、(3)的各自的步骤2中检测d的最大值d的流程图。

图6表示基本构成(1)、(2)、(3)的各自的步骤1～4之中、各自的自步骤2以后的步骤的流程图。

图7表示用于检测k个等幅区分区域中的各d的大小的顺序的流程图。

附图标记说明

1预定的造型对象物

2等幅区分区域

3等幅区分区域的边界上的截面

4各层叠区域

5中心位置

6外侧周围

具体实施方式

如图4所示，基本构成(1)、(2)、(3)在沿造型的高度方向将层叠区域4设定为多个等幅区分区域2这一点上是共通的。

通过设定这样的等幅区分区域2，能够选择该各区域中的层叠数n，进而能够选择各等幅区分区域2中的层叠单位的厚度。

在各等幅区分区域2的上下两侧必然存在边界，但在各等幅区分区域2中，处于上侧的边界截面3的形状相对于下侧的边界截面3的形状的变化越大则外侧周围6的沿长度方向的变化的程度越大的状态。

着眼于这样的状态，基本构成(1)、(2)、(3)与该变化的程度对应地选择了层叠数n。

具体而言，在基本构成(1)的情况下，如步骤1所记载的那样，将截面3的平均距离作为参数，在基本构成(2)的情况下，选择截面3的最大横向幅度与最大纵向幅度的总和作为参数，在基本构成(3)的情况下，选择距中心位置5的最大距离作为参数。

选择这些参数的根据在于：在各等幅区分区域2中，上侧截面3与下侧截面3的各参数之差越大，沿高度方向的各层叠截面3的变化的程度越大。

其结果，在基本构成(1)中，作为步骤1，对于预先设定好了造型的模型的等幅区分区域2中的形成上下两侧的边界的各截面3，通过cam或控制用计算机，采用直角坐标即(x，y)坐标，如图1(a)、(b)所示那样，由外侧周围6的各坐标(x1，y1)、…、(xi，yi)、…、(xh，yh)，通过

x0＝(x1+…+xi+…+xh)/h

y0＝(y1+…+yi+…+yh)/h

的运算来进行该各截面3的中心位置5的坐标(x0，y0)的计算，并且，对于从该中心位置5到形成外侧周围6的各坐标(x1，y1)、…、(xi，yi)、…、(xh，yh)的平均距离r，在进行

的计算后，通过

r＝(r1+…+ri+…+rh)/h

的运算来算出，

对于各等幅区分区域2，计算上侧的边界上的各截面3的所述平均距离与下侧的边界上的各截面3的所述平均距离之差的绝对值d；

在基本构成(2)中，采用了直角坐标即(x，y)坐标，对于预先设定好了造型的模型的等幅区分区域2中的形成上下两侧的边界的各截面3，通过cam或控制用计算机，如图2(a)、(b)所示那样，计算该各截面3的最大横向幅度与最大纵向幅度的总和，并且，对于各等幅区分区域2，计算上侧的边界上的各截面3的所述总和与下侧的边界上的各截面3的所述总和之差的绝对值d；

在基本构成(3)中，采用了旋转坐标即(r，θ)坐标，对于预先设定好了造型的模型的等幅区分区域2中的形成上下两侧的边界的各截面3，通过cam或控制用计算机，如图3(a)、(b)所示那样，由形成外侧周围的坐标(r1，θ1)、…、(ri，θi)、…、(rh，θh)，通过

r0＝(r1+…+ri+…+rh)/h

θ0＝(θ1+…+θi+…+θh)/h

的运算来算出该各截面3的中心位置5的坐标(r0，θ0)，关于从该中心位置5到形成外侧周围6的(r1，θ1)、…、(ri，θi)、…、(rh，θh)的距离，使已设定的(r，θ)坐标的原点(0,0)向上述(r0，θ0)的位置位移，并且，计算基于该位移而获得的新的中心位置(0,0)与各外侧周边的坐标位置之间的距离r1’、…、ri’、…、rh’，从基于该计算而获得的距离中选择最大距离，并且，对于各等幅区分区域2，计算上侧的边界上的各截面3的所述最大距离与下侧的边界上的各截面3的所述最大距离之差的绝对值d。

各截面3中的参数的计算，均通过cam或控制用计算机来实现，但在如基本构成(1)那样选择距中心位置5的平均距离作为参数的情况下，该参数能够极为准确地反映截面3的形状，与此相对，在如基本构成(2)那样选择最大横向幅度和最大纵向幅度作为参数的情况下、以及在如基本构成(3)那样选择距中心位置5的最大距离作为参数的情况下，不可否认在准确反映截面3的形状这一点上比基本构成(1)差。

但是，为了计算距中心位置5的平均距离，需要对各截面3中基于数字(digital)上的设计而形成于外侧周围6的所有点坐标，计算中心位置5，还需要计算距中心位置5的距离，但在通常的三维造型方法中，采用了直角坐标即(x，y)坐标，所以不得不需要基于勾股定理(毕达哥拉斯定理)来计算该平均距离。

即使通过采用旋转坐标即(r，θ)坐标，而不需要基于所述勾股定理进行计算，平均距离的计算仍是相当复杂的。

因此，基本构成(1)中的步骤1，与实际的造型时立即实现的情况相比较，更适合于事先按照各造型对象物1的模型来实现的情况。

与此相对，基本构成(2)的上述总和的计算、以及基本构成(3)的最大距离的计算，不需要多少时间，所以能够根据各造型对象物在实际的造型时立即实现d的计算。

基本构成(1)、(2)、(3)的各步骤1的计算分别如图1、2、3的流程图所示。

再者，在图3(b)的流程图中，

关于rl与rm的大小关系，立足于上侧的边界截面与下侧的边界截面共通这一基准，但其根据的当然的前提是，对于各等幅区分区域的上侧的边界截面以及下侧的边界截面中的坐标的数h，设定能够进行微细化到上侧的边界截面以及下侧的边界截面中的rl与rm的大小关系不逆转的程度的区分那样的数。

在执行了各步骤1之后，基本构成(1)、(2)、(3)的各步骤2、3、4均相同。

具体地说明，在步骤2中，设定设想d为0的情况的最小层叠数n1，另一方面，通过图5所示的流程图检测d的最大值d，设定形成有该最大值d的等幅区分区域2中的最大层叠数n2，在步骤3中，在最小值n1与最大值n2之间随着d变大而设定大的数值n，通过n＝[n]这一通式来选择层叠数n，在步骤4中，在实际的造型时，在各等幅区分区域2中基于通过步骤3所选择的层叠数n实行粉末层的形成以及烧结。

在步骤2中，通过设想d为0的情况，来设定了最小的层叠数n1，其根据在于：在诸多造型对象物1中，有在规定的高度幅度内在高度方向上截面3的形状没有变化的区域。

与此相对，在各等幅区分区域2的d中必定存在最大值d，在该情况下，等幅区分区域2内的截面3的形状的变化最大，所以设定了最大的层叠数n2。

在步骤3中，在最小值n1与最大值n2之间选择了反映了d的大小关系的层叠数n，但在该选择中，没有特别的限定，截面3的形状的变化的顺序需要反映层叠数的顺序。

在选择了这样的正整数的层叠数n后，基本构成(1)、(2)、(3)，如步骤4那样，将步骤1中的各等幅区分区域2沿上下方向进一步等幅区分成n个，而且设定了等幅区分出的各n个截面3的与在步骤1中预先设定好了造型的模型切合的外侧周围6的坐标。

上述外侧周围6的坐标的设定，可以通过将上述模型的形状记录于cam的存储器中后，通过cam来计算上述各等幅区分区域2中的n个进一步等幅区分所得的截面3的与上述模型切合的外侧周围区域6的各坐标而实现。

经过这样的步骤4，结果能够如步骤5那样，基于层叠数n实行粉末层的形成以及烧结，并且，针对切削工具的移动进行控制以使通过步骤4设定的外侧周围6的坐标位置成为最终的切削位置。

可以事先准备步骤1、2、3，然后进行实际的造型，或者，也可以从步骤1的阶段开始进行实际的造型，特别是关于基本构成(2)、(3)，如上所述，那样的方法也极为适合。

步骤2、3、4、5的各状况如图6的流程图所示。

作为步骤3中的正整数n的选择，最典型的方法是作为层叠数n采用

这一最小值n1与最大值n2的算术平均值。

作为上述层叠数n的选择，不仅可采用上述算术平均值，还可以采用

这一最小值n1与最大值n2之间的几何平均值。

在上述几何平均的情况下，能够与算术平均的情况同样地准确地反映各等幅区分区域2中的截面3的形状的变化。

作为层叠数n的选择，也可以采用上述算术平均值与上述几何平均值的中间值。

具体而言，选择正数a、b且a+b＝1，进行n＝a·(通过算术平均所得的n)+b·(通过几何平均所得的n)这一计算、或者n＝(通过算术平均所得的n)^a·(通过几何平均所得的n)^b这一计算即可。

有别于上述那样的算术平均或几何平均、以及它们的组合，也可以对于k个等幅区分区域2中的各等幅区分区域2的d，通过图7的流程图检测出d1≤d2≤…≤di≤…≤dk这一顺序后，采用

这一反映d的大小顺序的状态。

以下，通过实施例来进行说明。

实施例1

实施例1，其特征在于，根据各层叠的厚度，调整激光束或电子束的每单位面积的照射量。

在造型对象物1中，当然根据各区域的功能来调整了烧结的程度。

但是，在各等幅区分区域2中的层叠数n变化、其结果各层叠单位的厚度发生了变化的情况下，在各束的照射程度相同时，越是厚度薄的层叠单位，烧结的程度越大，无奈的是会发生不适于上述功能上的要求这样的弊害。

实施例1，为了避免这样的弊害，能够根据厚度的变化，来调整烧结的程度从而适合于各区域的功能上的要求。

实施例2

实施例2，其特征在于，在各层叠单位的截面3在与高度方向垂直的方向上为同一位置的情况下，各层叠单位的厚度越大，将每单位面积的照射量设定得越大。

在现实的三维造型对象物1的情况下，存在不少相同的烧结程度的区域。

在这样的情况下，根据基本构成(1)、(2)、(3)，各等幅区分区域2中的层叠数n、进而各层叠单位的厚度发生了变化的情况下，通过采用相同的烧结程度，反倒会得不到均一的烧结程度。

实施例2考虑到这样的状况，能够通过各层叠单位的厚度越大就使每单位面积的照射量越大，来实现均一的烧结程度。

产业上的利用可能性

从以上的说明明确可知，本发明能够与造型对象物的上下方向的截面形状的变化对应地设定适当的各层叠单位的厚度，能够在所有的三维造型中利用。