一种预规定瞬态性能的汽车主动悬架自适应控制方法与流程

本发明涉及一种预规定瞬态性能的汽车主动悬架自适应控制方法，属于车辆工程领域。

背景技术：

现代车辆所提供给驾驶员及乘客的驾驶舒适度不仅仅取决于整车的控制性能，汽车主动悬架同样是保证汽车舒适度的关键部件之一。主动悬架通过增加可实时控制的有源力辅助弹簧阻尼元件主动抑制因路面颠簸所带来的振动冲击，提高车辆稳定性、安全性和乘坐舒适度。然而在实际汽车主动悬架系统模型中，模型参数不确定性和建模误差无法避免，这些因素的存在将会极大的削弱主动悬架的性能。自适应控制虽可通过在线调整参数，降低模型不确定性对系统性能的影响。但在实际应用中，传统自适应控制依然存在一些问题，限制了其实际应用。

首先，当被控系统存在扰动或噪声时，传统自适应控制会引起参数漂移和系统不稳定的问题，进而降低主动悬架系统的性能。虽然已有的e修正法、σ修正法可有效克服了参数漂移问题，但此类修正项无法实现未知参数准确估计，而在理论上只能证明系统被估计参数收敛到其真值附近邻域内而非真值本身。基于此设计的控制器在实际车辆系统中会弱化汽车主动悬架的性能。其次，现有自适应控制难以保证瞬态控制收敛性能，无法保证在不同颠簸程度路面条件下控制器依旧可以快速做出响应维持车身稳定，并将车身颠簸控制在预先规定的范围内。因此，现有针对汽车主动悬架设计的自适应控制方法中，解决定量设计自适应控制误差收敛的瞬态性能，保证系统未知参数(如：车重和转动惯量)准确估计等问题的解决办法并不多，这在一定程度上限制了主动控制汽车悬架的实际应用。

技术实现要素：

本发明提供了一种预规定瞬态性能的汽车主动悬架自适应控制方法，将预设瞬态性能函数引入自适应控制时间中，并应用神经网络降低主动悬架模型不确定性对系统性能的影响，同时利用基于参数误差信息学习的自适应参数估计方法，构建基于参数误差信息的自适应学习律，进而更加准确地实时估计系统未知参数，解决传统自适应控制方法无法准确估计车辆未知参数、无法同时保证系统稳态和瞬态性能的问题，为提高车辆悬架系统控制精度、驾驶舒适度、安全性提供支持。

本发明的技术方案是：一种预规定瞬态性能的汽车主动悬架自适应控制方法，首先根据汽车动力学理论以及牛顿第二定律，建立半车主动悬架动力学模型；接着通过车载传感器测量计算得到汽车垂直方向位移和俯仰方向俯仰角；再对控制目标即汽车垂直方向位移以及汽车俯仰方向俯仰角进行误差转化操作；结合转化后的误差，引入神经网络补偿悬架动力学模型不确定性对系统的影响，进而设计汽车在垂直方向以及俯仰方向运动的控制动作；进一步对控制误差和系统递推向量进行滤波操作，提取参数估计误差，实现汽车垂直方向位移及俯仰方向俯仰角的瞬态、稳态控制，并满足主动悬架其他性能；用包含参数估计误差的向量设计自适应律；然后判断激励条件是否满足，若满足，根据估计得到的向量计算出汽车质量以及转动惯量的估计值；若不满足，则给路面扰动加入随机干扰，并返回重新测量。

所述方法的具体步骤如下：

Step1、建立半车主动悬架动力学模型：根据汽车动力学理论以及牛顿第二定律，对半车主动悬架进行受力分析，可得到半车主动悬架动力学模型如下：

其中，M是汽车质量，I是汽车俯仰运动时转动惯量，m_f为汽车前轮的簧下质量，m_r为汽车后轮的簧下质量；F_df为汽车前轮阻尼器阻尼力，F_dr为汽车后轮阻尼器阻尼力；F_sf为汽车前轮弹簧力，F_sr为汽车后轮弹簧力；F_tf为汽车前轮弹力，F_bf为汽车前轮阻尼力；F_tr为汽车后轮弹力，F_br为汽车后轮阻尼力；y_c为汽车垂直方向位移，为俯仰方向汽车俯仰角，y₁为汽车前轮簧下质量位移，y₂为汽车后轮簧下质量位移；a为汽车前主动悬架至汽车质心距离，b为汽车后主动悬架至汽车质心距离；u₁为汽车前主动悬架的输出力，u₂为汽车后主动悬架的输出力；u_y为汽车在垂直方向运动的控制动作，为汽车在俯仰方向运动的控制动作；

Step2、通过代数变换将半车主动悬架动力学模型转化为状态空间形式：

定义x₁＝y_c,x₅＝y₁,x₇＝y₂，则可得到：

其中，θ₁＝1/M为需要估计的汽车未知质量的倒数，θ₂＝1/I为需要估计的汽车未知转动惯量的倒数；

Step3、通过车载传感器测量计算得到汽车垂直方向位移y_c和俯仰方向俯仰角将其作为下面设计的控制方法的输入量；

Step4、对控制目标即汽车垂直方向位移x₁＝y_c进行误差转化操作：

Step4.1、定义一个光滑单调递减函数ψ(t),R⁺→R⁺为：

ψ(t)＝(ψ₀-ψ_∞)e^-αt+ψ_∞

其中，ψ₀为函数初值，ψ_∞为函数允许的稳态误差，e^-αt为指数函数常量，α为函数收敛速度，t表示时间，ψ₀与ψ_∞数值的选取应满足ψ₀＞ψ_∞；汽车垂直方向位移应满足如下边界条件：

其中，δ,为两个正常数；

Step4.2、定义另一个光滑严格单调递增函数z₁∈R，函数应满足条件如下：

其中，L_∞表示有界函数；

Step4.3、在得到性能方程ψ(t)和严格单调递减函数S(z₁)的基础上，汽车垂直方向位移表达为x₁＝ψS(z₁)，并通过代数变换将控制目标进行转换后的参数表达式为：

Step5、根据如下步骤设计汽车在垂直方向运动的控制动作u_y：

Step5.1、定义控制误差s_p1如下：

其中，Λ_p1＞0为正常数，T为矩阵转置运算符号，z₁为Step4.2中定义的数值变量(z₁为汽车垂直方向位移x₁转换后的误差变量)，为z₁对时间的导数；对s_p1进行求导运算可得：

其中，θ₁＝1/M为需要估计的汽车未知质量的倒数，为计算数值变量，为未知的动力学系统表达式；采用神经网络对T_p1(Z_p1)进行逼近，表达式如下：

其中，w_p1∈R⁵为神经网络未知权重，R^L_p为L_p维实空间，φ_p1(Z_p1)为神经网络基函数，Z_p1为神经网络输入变量，ε_p1∈R为神经网络误差；

Step5.2、设计控制汽车垂直方向位移的控制动作u_y，表达式如下：

其中，k_p1为一个正常数，为未知参数θ₁的估计值，为神经网络未知权重w_p1的估计值；

Step5.3、在采用神经网络逼近的基础上，控制误差导数可表达为如下参数化形式：

其中，是需要估计的未知参数向量，为系统递推向量，通过输入u_y和神经网络基函数φ_p1(Z_p1)计算获得的；

Step6、根据步骤Step4的方法对汽车俯仰方向俯仰角进行误差转化操作，再根据步骤Step5的方法，得到汽车在俯仰方向运动的控制动作表达式如下：

其中，为计算数值变量，为需要估计的汽车未知转动惯量的倒数θ₂＝1/I的估计值，k_p2为一个正常数，s_p2为控制误差，为神经网络未知权重w_p2的估计值，φ_p2(Z_p2)为神经网络基函数，Z_p2为神经网络输入变量；

Step7、对控制误差和系统递推向量进行滤波操作，提取参数估计误差，用于后续自适应律设计：

Step7.1、定义两个滤波变量s_p1f和Φ_p1f为：

其中，k是一个正常数；

Step7.2、定义辅助滤波矩阵P_p1∈R^6×6和滤波向量Q_p1∈R^6×1为：

其中，l是一个正常数；

Step7.3、在得到辅助变量P_p1和Q_p1基础上，计算出包含参数估计误差的向量H_p1∈R^6×1为：

其中，是未知参数向量W_p1的估计值；

Step8、用包含参数估计误差的向量H_p1设计自适应律，得到未知参数向量W_p1的估计值

其中，Γ_p1>0为学习速率，σ＞0为一个正常数；

Step9、计算矩阵P_p1最小特征值，并判断其是否大于0，来判断持续激励条件是否满足：

当矩阵P_p1最小特征值大于0，则执行步骤Step10；否则给路面扰动加入随机干扰，然后返回步骤Step3；

Step10、通过步骤Step1-Step9实现汽车垂直方向位移及汽车俯仰方向俯仰角的瞬态、稳态控制，并满足主动悬架其他性能；在获得未知参数向量估计值的基础上，通过求的倒数计算出汽车未知质量的估计值类似于Step7-Step9，设计自适应律获得俯仰方向未知参数的估计值然后通过求的倒数计算出汽车未知转动惯量的估计值

本发明的工作原理是：

1)建立半车主动悬架动力学模型，根据汽车动力学理论以及牛顿第二定律，对半车主动悬架进行受力分析，可得到半车主动悬架动力学模型如下：

其中，M是汽车质量，I是汽车俯仰运动时转动惯量，m_f为汽车前轮的簧下质量，m_r为汽车后轮的簧下质量；F_df为汽车前轮阻尼器阻尼力，F_dr为汽车后轮阻尼器阻尼力；F_sf为汽车前轮弹簧力，F_sr为汽车后轮弹簧力；F_tf为汽车前轮弹力，F_bf为汽车前轮阻尼力；F_tr为汽车后轮弹力，F_br为汽车后轮阻尼力；y_c为汽车垂直方向位移，为汽车俯仰角，y₁为汽车前轮簧下质量位移，y₂为汽车后轮簧下质量位移；a为汽车前主动悬架至汽车质心距离，b为汽车后主动悬架至汽车质心距离；u₁为汽车前主动悬架的输出力，u₂为汽车后主动悬架的输出力；u_y为汽车在垂直方向运动的控制动作，为汽车在俯仰方向运动的控制动作。

2)将半车主动悬架动力学模型转化为状态空间表达式形式：

定义x₁＝y_c,x₅＝y₁,x₇＝y₂,则可得到

其中，θ₁＝1/M为需要估计的汽车未知质量的倒数，θ₂＝1/I为需要估计的汽车未知的转动惯量的倒数；

3)通过车载传感器测量计算汽车车身垂直方向位移y_c和俯仰方向俯仰角

汽车行驶系统中可采用加速度计等对系统位移和偏转角度等进行测量，并进行积分处理可得到垂直方向位移y_c和俯仰方向俯仰角作为控制方法输入。

4)对控制目标变量(即汽车垂直方向位移)x₁＝y_c进行误差转化操作：

4.1)定义一个正的光滑单调递减函数ψ(t),R⁺→R⁺为：

ψ(t)＝(ψ₀-ψ_∞)e^-αt+ψ_∞

其中，ψ₀为函数初值，ψ_∞为函数允许的稳态误差范围，e^-αt为指数函数常量，α为函数收敛速度，t表示时间，ψ₀与ψ_∞数值的选取应满足ψ₀＞ψ_∞。则汽车垂直方向位移控制性能目标应满足如下边界条件：

其中，δ,为两个正常数。

4.2)定义另一个光滑严格单调递增函数z₁∈R，则汽车垂直方向位移误差目标表达为x₁＝ψS(z₁)，通过代数变换将控制目标误差进行转换后的参数表达式为：

5)设计汽车在垂直方向运动的控制动作u_y：

5.1)定义控制误差s_p1如下：

其中，Λ_p1＞0为正常数，T为矩阵转置运算符号，z₁为Step4.2中定义的数值变量，为z₁对时间的导数。对s_p1进行求导运算可得：

其中，θ₁＝1/M为需要估计的汽车未知质量的倒数为计算数值变量，为未知的动力学系统表达式；采用神经网络对T_p1(Z_p1)进行逼近，表达式如下：

其中，w_p1∈R⁵为神经网络未知权重，为L_p维实空间，φ_p1(Z_p1)为神经网络基函数，Z_p1为神经网络输入变量，ε_p1∈R为神经网络误差。

5.2)设计汽车在垂直方向运动的控制动作u_y，表达式如下：

其中，k_p1为一个正常数，为需要估计的汽车未知质量的倒数θ₁的估计值，为神经网络未知权重w_p1的估计值。

5.3)在采用神经网络逼近的基础上，控制误差导数可表达为如下形式：

其中，是需要估计的未知参数向量，为系统递推向量，可通过输入u_y和神经网络基函数φ_p1(Z_p1)计算获得的。

6)根据步骤4)的方法对控制目标汽车俯仰角进行误差转化操作，再根据步骤5)的方法，得到汽车在俯仰方向运动的控制动作表达式如下：

其中，为计算数值变量。为需要估计的未知转动惯量的倒数θ₂的估计值，k_p2为一个正常数，s_p2为控制误差，为神经网络未知权重w_p2的估计值，φ_p2(Z_p2)为神经网络基函数，Z_p2为神经网络输入变量；

7)对控制误差和系统递推向量进行滤波操作，提取参数估计误差，用于后续自适应律设计：

7.1)计算两个滤波变量s_p1f和Φ_p1f为：

其中，k是一个正常数。

7.2)计算辅助滤波矩阵P_p1∈R^6×6和滤波向量Q_p1∈R^6×1为

其中，l是一个正常数。

7.3)在获得P_p1和Q_p1的基础上，计算包含参数估计误差的向量H_p1∈R^6×1为：

其中，是未知参数向量W_p1的估计值。则可根据上述系统特性可验证：

可见，辅助变量H_p1包含参数估计误差信息实现了参数误差信息的提取。

8)运用参数估计误差H_p1设计用于参数估计的自适应律，得到未知参数向量W_p1的估计值

其中，Γ_p1>0为学习速率，σ＞0为一个正常数。

可证明，上述控制方法和自适应律可同时保证参数估计误差和系统控制误差s_p1一致最终有界。特别当神经网络误差为0时，参数估计误差和系统控制误差s_p1指数收敛到0。

9)验证参数估计收敛的条件：

可证明只要递推矩阵Φ_p1满足持续激励条件，则矩阵P_p1最小特征值大于0，则可保证上述8)中所示的自适应律可保证参数估计误差和系统控制误差指数收敛。故验证参数收敛条件(持续激励条件)可等价为验证矩阵P_p1最小特征值是否大于0。这也提供了一种可供操作的验证持续激励条件的方法。

10)根据得到的参数估计计算出车重和转动惯量的估计：

汽车系统中的未知参数变量(如：车重、转动惯量)可基于估计得到的向量和进行简单的数学变换导出，如：求的倒数可得到汽车未知质量M的估计值类似于7)-9)，可以设计自适应律获得俯仰方向未知参数的估计值然后通过求的倒数计算出汽车未知的转动惯量的估计值

本发明的有益效果是：

1、本发明提出了保证主动悬架瞬态性能的自适应控制方法，使汽车在路面干扰条件下的垂直方向位移和俯仰方向角度的稳态和瞬态控制误差收敛在预先规定的范围内，保证车身平稳进，提高驾驶舒适度的同时优化主动悬架系统其他性能(如执行机构较小的工作空间、较小的轮胎波动)。对比传统主动控制方法，本方法预先规定主动悬架的瞬态性能，可事先设计车身恢复平稳所需时间、允许车身最大颠簸等，会大大提升汽车悬架的性能。

2、本发明区别于传统自适应控制方法采用基于梯度的参数估计方法，本发明中采用参数估计误差信息来修正自适应律，可保证在满足持续激励条件下被估计的参数收敛至其真值，进一步提高控制精度。

3、本发明的鲁棒性能良好，可采用神经网络补偿系统未建模动态的影响，提高了控制器收敛速度和控制精度，改善了主动悬架性能，且适用于各种具有主动悬架车辆在各种未知路况的实时控制和估计、具有较广泛的实用性。

附图说明

图1为本发明所提供的用于构建半车主动悬架动力学模型的系统示意图；

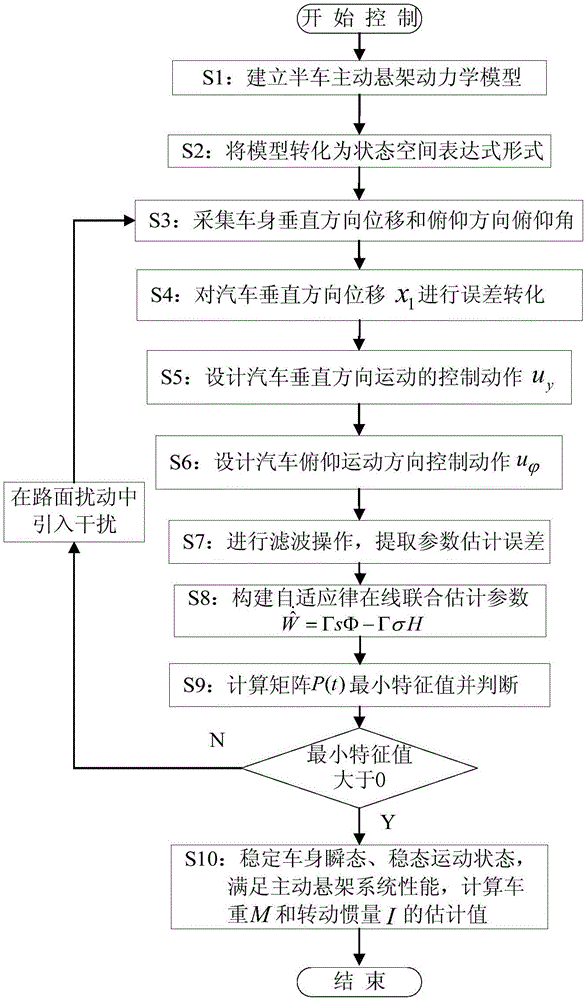
图2为本发明所提供的预规定瞬态性能的自适应控制方法的流程图；

图3为本发明应用实施例1中路面扰动情况效果图；

图4为本发明应用实施例1中对车辆运动状态控制效果图；

图5为本发明应用实施例1中车辆前后主动悬架运动空间效果图；

图6为本发明应用实施例1中车辆前轮与后轮位移波动效果图；

图7为本发明应用实施例1中对车重及转动惯量估计效果图；

图8为本发明应用实施例2中路面扰动情况效果图；

图9为本发明应用实施例2中对车辆运动状态控制效果图。

具体实施方式

实施例1：如图1-7所示，一种预规定瞬态性能的汽车主动悬架自适应控制方法，所示方法的具体步骤如下：

按照上述发明所述流程对一类典型的中型车以45km/h的车速行驶经过正弦弹跳路面时保持车身平稳和满足主动悬架性能要求进行了控制，并在Matlab软件中进行了数值模拟。

Step1、建立半车主动悬架动力学模型：根据汽车动力学理论以及牛顿第二定律，对半车主动悬架进行受力分析，可得到半车主动悬架动力学模型如下；

其中，M＝1200kg是汽车质量，I＝600kgm²是汽车俯仰运动时转动惯量，m_f＝100kg为汽车前轮的簧下质量，m_r＝100kg为汽车后轮的簧下质量；F_df为汽车前轮阻尼器阻尼力，F_dr为汽车后轮阻尼器阻尼力；F_sf为汽车前轮弹簧力，F_sr为汽车后轮弹簧力；F_tf为汽车前轮弹力，F_bf为汽车前轮阻尼力；F_tr为汽车后轮弹力，F_br为汽车后轮阻尼力；y_c为汽车垂直方向位移，为汽车俯仰方向俯仰角，y₁为汽车前轮簧下质量位移，y₂为汽车后轮簧下质量位移；a＝1.2m为汽车前主动悬架至汽车质心距离，b＝1.5m为汽车后主动悬架至汽车质心距离；u₁为汽车前主动悬架的输出力，u₂为汽车后主动悬架的输出力；u_y为汽车在垂直方向运动的控制动作，为汽车在俯仰方向运动的控制动作。在Matlab数值分析部分，主动悬架非线性硬弹簧、分段阻尼器及汽车轮胎的力学表达式如下：

F_tf＝k_f2(y₁-y_o1),F_tr＝k_r2(y₂-y_o2)

其中，k_f1＝15,000N/m为前轮弹簧线性项刚度系数，k_r1＝15,000N/m为后轮弹簧线性项刚度系数；k_nf1＝1000N/m为前轮弹簧非线性项刚度系数，k_nr1＝1000N/m为后轮弹簧非线性项刚度系数；b_e1＝b_e2＝1500Ns/m为阻尼器伸展运动系数，b_c1＝b_c2＝1200Ns/m为阻尼器压缩运动系数；汽车前轮的刚度系数为k_f2＝200,000N/m，汽车前轮的阻尼系数为b_f2＝1500Ns/m；汽车后轮的刚度系数为k_r2＝150，000N/m，汽车后轮的阻尼系数为b_r2＝2000Ns/m，y_o1为汽车前轮所受路面扰动，y_o2为汽车后轮所受路面扰动，在本实例中由Carsim仿真软件模拟真实路面给出。为汽车前轮弹簧位移量，为汽车后轮弹簧位移量。

Step2、通过代数变换将半车主动悬架动力学模型转化为状态空间形式：

定义x₁＝y_c,x₅＝y₁,x₇＝y₂,则可得到

其中，θ₁＝1/M为需要估计的汽车未知质量的倒数，θ₂＝1/I为需要估计的汽车未知的转动惯量的倒数；

Step3、通过车载传感器测量计算得到汽车车身垂直方向位移y_c和俯仰方向俯仰角本实施案例中，路面扰动设置为正弦弹跳路面扰动；

Step4、对控制目标汽车垂直方向位移x₁进行误差转化操作：

Step4.1、定义一个正的光滑单调递减函数ψ(t),R⁺→R⁺为：

ψ(t)＝(ψ₀-ψ_∞)e^-αt+ψ_∞

其中，性能函数初值ψ₀＝0.012，允许的稳态误差范围ψ_∞＝0.0014，函数收敛速度α＝9。汽车垂直方向位移这一控制目标应满足如下边界条件：

其中，为两个正常数。

Step4.2、定义严格单调递减光滑函数z₁∈R，满足条件：

Step4.3、在得到性能方程ψ(t)和严格单调递减函数S(z₁)的基础上，汽车垂直方向位移表达为x₁＝ψS(z₁)，并通过代数变换将控制目标误差进行转换后的参数表达式为：

Step5、根据如下步骤设计汽车在垂直方向运动的控制动作u_y：

Step5.1、定义控制误差s_p1如下：

其中，Λ_p1＝50为常数。T为矩阵转置运算符号，z₁为Step4.2中定义的数值变量，为z₁对时间的导数。对s_p1进行求导运算可得：

其中，θ₁＝1/M为需要估计的汽车未知质量的倒数；为计算数值变量，为未知的动力学系统表达式；采用神经网络对T_p1(Z_p1)进行逼近，表达式如下：

其中，w_p1∈R⁵为神经网络未知权重，为维实数空间，φ_p1(Z_p1)为神经网络基函数，Z_p1为神经网络输入变量，ε_p1∈R为神经网络误差。

Step5.2、设计控制汽车垂直方向位移的控制动作u_y，表达式如下：

其中，k_p1＝700为一个正常数，为需要估计的汽车未知质量的倒数θ₁的估计值，为神经网络未知权重w_p1的估计值。

Step5.3、在采用神经网络逼近的基础上，控制误差导数可表达为如下参数化形式：

其中，是需要估计的未知参数向量，为系统递推向量，可通过输入u_y和神经网络基函数φ_p1(Z_p1)计算获得的。

Step6、根据步骤Step4的方法对汽车的俯仰角进行误差转化操作，再根据步骤Step5的方法，得到汽车在俯仰方向运动的控制动作表达式如下：

其中，为计算数值变量。为需要估计的未知转动惯量的倒数θ₂的估计值，k_p2＝700，s_p2为控制误差，为神经网络未知权重w_p2的估计值，φ_p2(Z_p2)为神经网络基函数，Z_p2为神经网络输入变量；俯仰方向控制器采用的其他相关的控制参数为ψ₀＝0.012，ψ_∞＝0.003，α＝8，Λ_p2＝80。

Step7、对控制误差和系统递推向量进行滤波操作，提取参数估计误差，用于后续自适应律设计：

Step7.1、定义两个滤波变量s_p1f和Φ_p1f为：

其中，k＝0.001是一个正常数。

Step7.2、定义辅助滤波矩阵P_p1∈R^6×6和滤波向量Q_p1∈R^6×1为：

其中，l＝1是一个正常数；

Step7.3、在得到辅助变量P_p1和Q_p1基础上，计算出包含参数估计误差的向量H_p1∈R^6×1为：

其中，是未知参数向量W_p1的估计值；可知，成立，故向量H_p1包含参数估计误差信息

Step8、用包含参数估计误差的向量H_p1设计自适应律，得到半车主动悬架动力学模型中未知参数向量W_p1的估计值

其中，Γ_p1＝60×diag[2.4,3.9,1000,10120,270,3250,0.0000000000165]为学习速率，σ＝0.001为一正常数。针对汽车俯仰运动设计的参数估计自适应律中的学习速率Γ_p2＝60×diag[2.2,1270,13500,1.6,300,2070,0.0000000000235]。

Step9、计算矩阵P_p1最小特征值，并判断其是否大于0，来判断持续激励条件是否满足：

在本实施案例中，可计算得知矩阵P_p1的最小特征值大于0，故执行步骤Step10；

Step10、通过步骤Step1-Step9实现汽车垂直方向位移及汽车俯仰方向俯仰角的瞬态、稳态控制，并满足主动悬架其他性能；在获得未知参数向量W_p1的估计值的基础上，通过求的倒数计算出汽车未知质量的估计值类似于Step7-Step9，可以设计自适应律获得俯仰方向未知参数的估计值然后通过求的倒数计算出汽车未知的转动惯量的估计值

根据上述实施流程，可获得该案例仿真结果如图3-图7。图3为在Carsim软件中所选取的测试路面扰动y_o1，y_o2。图4为控制汽车垂直方向位移与俯仰方向俯仰角在不同控制方法作用下的对比，可见相比于传统自适应控制方法，预规定瞬态性能的自适应控制方法可以获得更好的控制效果，在较短的时间内保持汽车车身平稳，控制误差(即车身垂直方向位移和俯仰方向俯仰角)均在预先规定的范围内。图5为主动悬架的机械机构运动空间限制。通过计算，受控的前后主动悬架运动空间均小于其运动位置的极限值，分别为Δy_{f max}＝0.1323m和Δy_{r max}＝0.1362m。图6为汽车前轮与后轮的位移波动情况，从图6可见所采用的预规定瞬态性能的自适应控制方法可以保证汽车前后轮胎的波动均小于其极限值，即|TD_{f max}|≤0.2078m和|TD_rmax|≤0.2085m，可在保证车辆的驾驶安全。图7为估计出的汽车质量和转动惯量与其真实值对比，可见估计出的数值基本收敛至其真值附近。上述实施案例数值仿真结果表明，本发明所提出控制方法能够明显的提升主动悬架的性能特性，在提供更好的驾驶舒适度的同时能够保证主动悬架其他性能，并且能有效估计出车身质量和转动惯量。这些参数的获得可进一步为汽车控制系统实施提供参考，并为汽车安全系统操作提供数据支持。

实施例2：如图8-9所示，一种预规定瞬态性能的汽车主动悬架自适应控制方法，所示方法的具体步骤如下：

按照上述发明所述流程对一类典型的中型车以60km/h的车速行驶经过长1200m的随机粗糙路面，保持汽车在行驶过程中的瞬态和稳态性能要求进行了控制，并在Matlab软件中进行了数值模拟。

Step1、建立半车主动悬架动力学模型，根据汽车动力学理论以及牛顿第二定律，对半车主动悬架进行受力分析，可得到半车主动悬架动力学模型如下

其中，M＝1200kg是汽车质量，I＝600kgm²是汽车俯仰运动时转动惯量，m_f＝100kg为汽车前轮的簧下质量，m_r＝100kg为汽车后轮的簧下质量；F_df为汽车前轮阻尼器阻尼力，F_dr为汽车后轮阻尼器阻尼力；F_sf为汽车前轮弹簧力，F_sr为汽车后轮弹簧力；F_tf为汽车前轮弹力，F_bf为汽车前轮阻尼力；F_tr为汽车后轮弹力，F_br为汽车后轮阻尼力；y_c为汽车垂直方向位移，为汽车俯仰角，y₁为汽车前轮簧下质量位移，y₂为汽车后轮簧下质量位移；a＝1.2m为汽车前主动悬架至汽车质心距离，b＝1.5m为汽车后主动悬架至汽车质心距离；u₁为汽车前主动悬架的输出力，u₂为汽车后主动悬架的输出力；u_y为汽车在垂直方向运动的控制动作，为汽车在俯仰方向运动的控制动作。在Matlab数值分析部分，主动悬架非线性硬弹簧、分段阻尼器及汽车轮胎的力学表达式如下：

F_tf＝k_f2(y₁-y_o1),F_tr＝k_r2(y₂-y_o2)

其中，k_f1＝15,000N/m为前轮弹簧线性项刚度系数，k_r1＝15,000N/m为后轮弹簧线性项刚度系数；k_nf1＝1000N/m为前轮弹簧非线性项刚度系数，k_nr1＝1000N/m为后轮弹簧非线性项刚度系数；b_e1＝b_e2＝1500Ns/m为阻尼器伸展运动系数，b_c1＝b_c2＝1200Ns/m为阻尼器压缩运动系数；汽车前轮的刚度系数为k_f2＝200,000N/m，汽车前轮的阻尼系数为b_f2＝1500Ns/m；汽车后轮的刚度系数为k_r2＝150，000N/m，汽车后轮的阻尼系数为b_r2＝2000Ns/m。在本实例中由Carsim仿真软件模拟真实路面给出。为汽车前轮弹簧位移量，为汽车后轮弹簧位移量。

Step2、通过代数变换将半车主动悬架动力学模型转化为状态空间形式：

定义x₁＝y_c,x₅＝y₁,x₇＝y₂,则可得到

其中，θ₁＝1/M为需要估计的汽车未知质量的倒数，θ₂＝1/I为需要估计的汽车未知的转动惯量的倒数；

Step3、通过车载传感器测量计算得到汽车车身垂直方向位移y_c和俯仰方向俯仰角本实施案例中，路面扰动设置为随机粗糙路面路况；

Step4、对控制目标汽车垂直方向位移x₁进行误差转化操作：

Step4.1、定义一个正的光滑单调递减函数ψ(t),R⁺→R⁺为：

ψ(t)＝(ψ₀-ψ_∞)e^-αt+ψ_∞

其中，性能函数初值ψ₀＝0.012，允许的稳态误差ψ_∞＝0.00002，函数收敛速度α＝9。

本实施案例中，对比实施案例1改变了稳态的收敛边界，预规定了更小、更接近0的稳态收敛边界。目的使汽车在行驶过程中，汽车主动悬架能够适用各种随机路面状况，并尽可能保持车身稳定状态、减少颠簸，从而为驾驶员及乘客提供更好的驾驶舒适度及平稳性。

汽车垂直方向位移控制目标应满足如下边界条件：

其中，为两个正常数。

Step4.2、定义严格单调递减光滑函数z₁∈R，满足条件：

Step4.3、在得到性能方程ψ(t)和严格单调递减函数S(z₁)的基础上，汽车垂直方向位移误差表达为x₁＝ψS(z₁)，并通过代数变换将控制目标误差进行转换后的参数表达式为：

Step5、根据如下步骤设计汽车在垂直方向运动的控制动作u_y，

Step5.1、定义滤波误差s_p1如下：

其中，Λ_p1＝50为正常数。T为矩阵转置运算符号，z₁为Step4.2中定义的数值变量，为z₁对时间的导数。对s_p1进行求导运算可得：

其中，θ₁＝1/M为需要估计的汽车未知质量的倒数，为计算数值变量，为未知的动力学系统表达式；采用神经网络对T_p1(Z_p1)进行逼近，表达式如下：

其中，w_p1∈R⁵为神经网络未知权重，为L_p维实数空间，φ_p1(Z_p1)为神经网络基函数，Z_p1为神经网络输入变量，ε_p1∈R为神经网络误差。

Step5.2、设计控制汽车垂直方向位移的控制动作u_y，表达式如下：

其中，k_p1＝700为一个正常数，为需要估计的汽车未知质量的倒数θ₁的估计值，为神经网络未知权重w_p1的估计值。

Step5.3、在采用神经网络逼近的基础上，控制误差导数可表达为如下参数化形式：

其中，是需要估计的未知参数向量，为系统递推向量，可通过输入u_y和神经网络基函数φ_p1(Z_p1)计算获得的。

Step6、根据步骤Step4的方法对汽车俯仰角进行误差转化操作，再根据步骤Step5的方法，得到汽车在俯仰方向运动的控制动作表达式如下：

其中，为计算数值变量。为需要估计的未知转动惯量的倒数θ₂的估计值，k_p2＝700，s_p2为控制误差，为神经网络未知权重w_p2的估计值，φ_p2(Z_p2)为神经网络基函数，Z_p2为神经网络输入变量；俯仰方向控制器采用的其他相关的控制参数为：ψ₀＝0.012，ψ_∞＝0.00002，α＝9，Λ_p2＝80。

Step7、对控制误差和系统递推向量进行滤波操作，提取参数估计误差，用于后续自适应律设计：

Step7.1、定义两个滤波变量s_p1f和Φ_p1f为：

其中，k＝0.001是正常数。

Step7.2、定义辅助滤波矩阵P_p1∈R^6×6和滤波向量Q_p1∈R^6×1为：

其中，l＝1是正常数。

Step7.3、在得到辅助变量P_p1和Q_p1基础上，计算出包含参数估计误差的向量H_p1∈R^6×1为：

其中，是未知参数向量W_p1的估计值；可知，成立，故向量H_p1包含参数估计误差信息

Step8、用包含参数估计误差的向量H_p1设计自适应律，得到半车主动悬架动力学模型中未知参数向量W_p1的估计值

其中，Γ_p1＝60×diag[2.4,3.9,1000,10120,270,3250,0.0000000000165]为学习速率，σ＝0.001为一正常数。针对汽车俯仰方向运动设计的参数估计自适应律中的学习速率Γ_p2＝60×diag[2.2,1270,13500,1.6,300,2070,0.0000000000235]。

Step9、计算矩阵P_p1最小特征值，并判断其是否大于0，来判断持续激励条件是否满足：

在本实施案例中，可计算得知矩阵P_p1的最小特征值大于0，故执行步骤Step10；

Step10、通过步骤Step1-Step9实现汽车垂直方向位移及汽车俯仰方向俯仰角的瞬态、稳态控制，并满足主动悬架其他性能；在获得未知参数向量W_p1的估计值的基础上，通过求的倒数计算出汽车未知质量的估计值类似于Step7-Step9，可以设计自适应律获得俯仰方向未知参数的估计值然后通过求的倒数计算出汽车未知的转动惯量的估计值

根据上述实施流程，可获得该案例仿真结果如图8-图9。图8为在Carsim软件中所选取的随机粗糙路面的扰动。图9为控制汽车垂直方向位移与俯仰方向俯仰角在采用不同控制方法情况下的对比，可见相比于传统自适应控制方法，预规定瞬态性能的自适应控制方法可以获得更好的控制效果，可以在更快的时间内保持汽车车身平稳，控制误差(即车身垂直方向位移和俯仰方向俯仰角)在瞬态和稳态时均在预先规定的范围内。本发明所提出的控制方法能有效提升主动悬架总体性能，相比实施例1中的路面扰动，本实施例中通过采取随粗糙路面路况，进一步验证所提出的控制方法在实际应用中的效果。

实施例3：一种预规定瞬态性能的汽车主动悬架自适应控制方法，首先根据汽车动力学理论以及牛顿第二定律，建立半车主动悬架动力学模型；接着通过车载传感器测量计算得到汽车垂直方向位移和俯仰方向俯仰角；再对控制目标即汽车垂直方向位移以及汽车俯仰方向俯仰角进行误差转化操作；结合转化后的误差，引入神经网络补偿悬架动力学模型不确定性对系统的影响，进而设计汽车在垂直方向以及俯仰方向运动的控制动作；进一步对控制误差和系统递推向量进行滤波操作，提取参数估计误差，实现汽车垂直方向位移及俯仰方向俯仰角的瞬态、稳态控制，并满足主动悬架其他性能；用包含参数估计误差的向量设计自适应律；然后判断激励条件是否满足，若满足，根据估计得到的向量计算出汽车质量以及转动惯量的估计值；若不满足，则给路面扰动加入随机干扰，并返回重新测量。

所述方法的具体步骤如下：

Step1、建立半车主动悬架动力学模型：根据汽车动力学理论以及牛顿第二定律，对半车主动悬架进行受力分析，可得到半车主动悬架动力学模型如下：

其中，M是汽车质量，I是汽车俯仰运动时转动惯量，m_f为汽车前轮的簧下质量，m_r为汽车后轮的簧下质量；F_df为汽车前轮阻尼器阻尼力，F_dr为汽车后轮阻尼器阻尼力；F_sf为汽车前轮弹簧力，F_sr为汽车后轮弹簧力；F_tf为汽车前轮弹力，F_bf为汽车前轮阻尼力；F_tr为汽车后轮弹力，F_br为汽车后轮阻尼力；y_c为汽车垂直方向位移，为俯仰方向汽车俯仰角，y₁为汽车前轮簧下质量位移，y₂为汽车后轮簧下质量位移；a为汽车前主动悬架至汽车质心距离，b为汽车后主动悬架至汽车质心距离；u₁为汽车前主动悬架的输出力，u₂为汽车后主动悬架的输出力；u_y为汽车在垂直方向运动的控制动作，为汽车在俯仰方向运动的控制动作；

Step2、通过代数变换将半车主动悬架动力学模型转化为状态空间形式：

定义x₁＝y_c,x₅＝y₁,x₇＝y₂，则可得到：

其中，θ₁＝1/M为需要估计的汽车未知质量的倒数，θ₂＝1/I为需要估计的汽车未知转动惯量的倒数；

Step3、通过车载传感器测量计算得到汽车垂直方向位移y_c和俯仰方向俯仰角将其作为下面设计的控制方法的输入量；

Step4、对控制目标即汽车垂直方向位移x₁＝y_c进行误差转化操作：

Step4.1、定义一个光滑单调递减函数ψ(t),R⁺→R⁺为：

ψ(t)＝(ψ₀-ψ_∞)e^-αt+ψ_∞

其中，ψ₀为函数初值，ψ_∞为函数允许的稳态误差，e^-αt为指数函数常量，α为函数收敛速度，t表示时间，ψ₀与ψ_∞数值的选取应满足ψ₀＞ψ_∞；汽车垂直方向位移应满足如下边界条件：

其中，δ,为两个正常数；

Step4.2、定义另一个光滑严格单调递增函数z₁∈R，函数应满足条件如下：

其中，L_∞表示有界函数；

Step4.3、在得到性能方程ψ(t)和严格单调递减函数S(z₁)的基础上，汽车垂直方向位移表达为x₁＝ψS(z₁)，并通过代数变换将控制目标进行转换后的参数表达式为：

Step5、根据如下步骤设计汽车在垂直方向运动的控制动作u_y：

Step5.1、定义控制误差s_p1如下：

其中，Λ_p1＞0为正常数，T为矩阵转置运算符号，z₁为Step4.2中定义的数值变量，为z₁对时间的导数；对s_p1进行求导运算可得：

其中，θ₁＝1/M为需要估计的汽车未知质量的倒数，为计算数值变量，为未知的动力学系统表达式；采用神经网络对T_p1(Z_p1)进行逼近，表达式如下：

其中，w_p1∈R⁵为神经网络未知权重，为L_p维实空间，φ_p1(Z_p1)为神经网络基函数，Z_p1为神经网络输入变量，ε_p1∈R为神经网络误差；

Step5.2、设计控制汽车垂直方向位移的控制动作u_y，表达式如下：

其中，k_p1为一个正常数，为未知参数θ₁的估计值，为神经网络未知权重w_p1的估计值；

Step5.3、在采用神经网络逼近的基础上，控制误差导数可表达为如下参数化形式：

其中，是需要估计的未知参数向量，为系统递推向量，通过输入u_y和神经网络基函数φ_p1(Z_p1)计算获得的；

Step6、根据步骤Step4的方法对汽车俯仰方向俯仰角进行误差转化操作，再根据步骤Step5的方法，得到汽车在俯仰方向运动的控制动作表达式如下：

其中，为计算数值变量，为需要估计的汽车未知转动惯量的倒数θ₂＝1/I的估计值，k_p2为一个正常数，s_p2为控制误差，为神经网络未知权重w_p2的估计值，φ_p2(Z_p2)为神经网络基函数，Z_p2为神经网络输入变量；

Step7、对控制误差和系统递推向量进行滤波操作，提取参数估计误差，用于后续自适应律设计：

Step7.1、定义两个滤波变量s_p1f和Φ_p1f为：

其中，k是一个正常数；

Step7.2、定义辅助滤波矩阵P_p1∈R^6×6和滤波向量Q_p1∈R^6×1为：

其中，l是一个正常数；

Step7.3、在得到辅助变量P_p1和Q_p1基础上，计算出包含参数估计误差的向量H_p1∈R^6×1为：

其中，是未知参数向量W_p1的估计值；

Step8、用包含参数估计误差的向量H_p1设计自适应律，得到未知参数向量W_p1的估计值

其中，Γ_p1>0为学习速率，σ＞0为一个正常数；

Step9、计算矩阵P_p1最小特征值，并判断其是否大于0，来判断持续激励条件是否满足：

当矩阵P_p1最小特征值不大于0，则给路面扰动加入随机干扰，然后返回步骤Step3，直到矩阵P_p1最小特征值大于0，则执行步骤Step10；

Step10、通过步骤Step1-Step9实现汽车垂直方向位移及汽车俯仰方向俯仰角的瞬态、稳态控制，并满足主动悬架其他性能；在获得未知参数向量估计值的基础上，通过求的倒数计算出汽车未知质量的估计值类似于Step7-Step9，设计自适应律获得俯仰方向未知参数的估计值然后通过求的倒数计算出汽车未知转动惯量的估计值

上面结合图对本发明的具体实施方式作了详细说明，但是本发明并不限于上述实施方式，在本领域普通技术人员所具备的知识范围内，还可以在不脱离本发明宗旨的前提下作出各种变化。