基于速度区间插值的间接式胎压监测标定方法与流程

1.本发明涉及轮胎胎压间接监测技术领域，特别是涉及一种基于速度区间插值的间接式胎压监测标定方法。


背景技术：

2.随着科技水平的不断进步，各种车辆已经成为人们生活中必不可少的交通工具。近年来，车辆安全问题愈加严重，人们对于车辆安全性能的关注也越来越高。其中，以abs/esc为基础的主动安全概念受到越来越多汽车厂商以及消费者的关注。在汽车领域中，轮胎的安全问题一直占据及其重要的地位。统计表明，在高速行驶中，如果车速超过160公里/小时，前轮爆胎时，车内人员的生存几率几乎为零。而交通事故中爆胎原因所占的比例高达60％，这其中75％的爆胎都是由胎压不足造成，且轮胎欠压对于油耗和轮胎寿命都有影响。因此，对轮胎胎压的实时监测显得及其重要。
3.胎压监测技术主要包括直接式胎压监测技术dtpms与间接式胎压监测技术itpms。目前，itpms对于胎压的分析主要有两部分，分别为时域分析tda和频域分析fda。其中，tda是根据车轮之间的轮速差异对车轮的相对车轮滚动半径进行计算；fda则是计算每个车轮的角速度频谱特征。在车辆自学习阶段完成之后，用实时监测到的tda和fda分析结果与学习阶段的值做比较，从而得出胎压的相对变化情况。
4.由于tda和fda的分析都与车速相关，所以学习阶段所存的值是分速度区间来存储的。在车辆自学习完成之后，实时计算的tda和fda分析结果也是与相同速度区间的标定值进行比较。在这种情况下itpms的监测报警功能只能在完成学习的速度区间中实现，这不符合实际应用时车辆对itpms功能的需求。在工程设计上需要根据速度区间划分标定界限，但对于itpms的用户来讲，这一划分规则是隐性的，客户在使用itpms进行自学习时，车辆极有可能在短时间内无法完成所有主要速度区间的学习，使得itpms不能在未学习的速度区间提供应有的监测报警功能。
5.因此，设计一种能够解决车辆的itpms系统在学习阶段无法完成所有主要速度区间的学习时导致的itpms系统不能在未学习的速度区间提供应有的报警功能的问题的基于速度区间插值的间接式胎压监测标定方法就很有必要。


技术实现要素：

6.为了克服上述问题，本发明提供一种基于速度区间插值的间接式胎压监测标定方法，将同一车辆的速度根据大小划分出不同的速度区间，并通过学习阶段的原始标定值拟合出各个速度区间之间的关系。从而根据车辆当前速度所属速度区间计算出可插入区间的标定值，并将计算的标定值与该速度区间的原始标定值作对比，从而判断轮胎是否出现异常。这种方法能够实现实时采集的tda及fda跨速度区间的插值判断，解决了车辆的itpms系统在学习阶段无法完成所有主要速度区间的学习时导致的itpms系统不能在未学习的速度区间提供应有的报警功能的问题。
7.为实现上述的目的，本发明采用的技术方案是：
8.一种基于速度区间插值的间接式胎压监测标定方法，包括以下步骤：
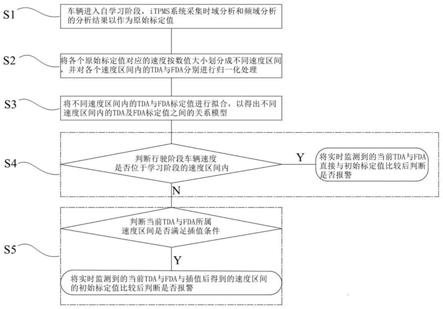
9.s1、车辆进入自学习阶段，itpms系统采集时域分析和频域分析的分析结果以作为原始标定值；
10.s2、将各个原始标定值对应的速度按数值大小划分成不同速度区间，并对各个速度区间内的时域分析标定值与频域分析标定值分别进行归一化处理；
11.s3、将不同速度区间内的时域分析标定值与频域分析标定值进行拟合，以得出不同速度区间内的时域分析标定值及频域分析标定值之间的关系模型；
12.s4、判断行驶阶段车辆速度是否位于学习阶段的速度区间内，若是，将实时监测到的当前时域分析实时值与频域分析实时值直接与初始标定值比较后判断是否报警；若不是，则执行s5；
13.s5、判断当前时域分析实时值与频域分析实时值所属速度区间是否满足插值条件，若是，则将实时监测到的当前时域分析实时值与频域分析实时值与插值后得到的速度区间的初始标定值比较后判断是否报警。
14.进一步的，车辆自学习阶段的时间不小于20min，并在平整光滑的路面上进行，以保证后续实时采样数据能满足插值条件。
15.进一步的，在步骤s2中，将样本点划分为七个速度区间，并将各个速度区间内的时域分析标定值与频域分析标定值分别进行归一化处理：
[0016][0017]
式中，是修正后的标定值，v是原始值，μ是所有原始值的平均值，σ是所有原始值的标准差。
[0018]
进一步的，步骤s3包括以下步骤：
[0019]
s31、将归一化后的时域分析标定值与频域分析标定值采用梯度下降的方法进行多项式拟合：
[0020]
y＝θ0+θ1x+θ2x2+θ3x3+θ4x4+θ5x5+θ6x6+θ7x7[0021]
式中，x为每一个样本点对应的速度区间，y为每一个样本点对应的标定值，θ0至θ7为需要进行拟合的参数；
[0022]
s32、采用随机数对参数θ0至θ7进行初始化，并将其整合成参数矩阵：
[0023]
θ＝[θ
0 θ
1 θ
2 θ
3 θ
4 θ
5 θ
6 θ7]
[0024]
s33、将所有样本点的速度区间x整合成输入矩阵：
[0025][0026]
式中，m为所有样本点的个数；
[0027]
s34、将所有样本点的标定值整合成输出矩阵：
[0028]
y＝[y1ꢀ…ꢀ
y
m
]
[0029]
s35、将参数矩阵、输入矩阵以及输出矩阵带入拟合关系式，并采用梯度下降法求解θ：
[0030][0031]
将上式整合为：
[0032][0033]
s36、对s35中整合后的拟合公式进行误差分析，以得出最优化的拟合曲线。
[0034]
进一步的，在步骤s36中，误差分析包括以下步骤：
[0035]
s361、对s35中整合后的拟合公式的因变量进行误差预测，并定义损失函数：
[0036][0037]
式中，为拟合值与实际值之间的误差；
[0038]
s362、对参数矩阵θ进行梯度计算：
[0039][0040]
s363、对参数矩阵θ进行更新：
[0041]
θ＝θ
‑
αdθ
[0042]
式中，α为学习速率，并取值0.1；
[0043]
s364、重复步骤s363，直至开始收敛，并将此时的参数矩阵θ记作设此时的拟合曲线方程为：
[0044][0045]
s365、根据上述拟合曲线方程计算不同速度区间下标定值的差值，得出差值公式：
[0046]
δv
j
＝f(j+1)
‑
f(j)，j∈[1，6]。
[0047]
进一步的，步骤s4包括以下步骤：
[0048]
s41、abs系统监测当前车辆行驶速度，并寻找其对应的速度区间；
[0049]
s42、读出步骤s41的速度区间内是否存在原始标定值；
[0050]
s43、若是，将实时监测到的当前时域分析实时值与频域分析实时值直接与原始标定值比较后判断是否报警；若不是，则执行s5。
[0051]
进一步的，在步骤s5中，所述插值条件包括部分速度区间在学习阶段采集到满足标定个数的原始标定值、以及不是跨超过两个的速度区间进行插值。
[0052]
进一步的，满足标定个数的原始标定值为单个速度区间的时域分析标定值个数大于25、以及频域分析标定值个数大于30，在此条件下可将实测值插入至其所述速度区间的相邻两个速度区间内进行比较。
[0053]
进一步的，满足标定个数的原始标定值为两个速度区间的时域分析标定值个数大于10、以及频域分析标定值个数大于15，或者，两个速度区间的时域分析标定值个数之和大于30、以及频域分析标定值个数之和大于45，在此条件下可将实测值插入至其所述速度区间的相邻两个速度区间以及相隔一个速度区间的速度区间内进行比较。
[0054]
进一步的，当任意一个速度区间的时域分析标定值个数大于25且频域分析标定值个数大于30时，不再使用插值后的值作为当前速度区间的标定值，而是使用当前速度区间
自身样本点计算出的值作为标定值。
[0055]
与现有技术相比，本发明的有益效果是：
[0056]
1.本发明的基于速度区间插值的间接式胎压监测标定方法，通过将同一车辆的速度根据大小划分出不同的速度区间，并通过学习阶段的原始标定值拟合出各个速度区间之间的关系。从而根据车辆当前速度所属速度区间计算出可插入区间的标定值，并将计算的标定值与该速度区间的原始标定值作对比，从而判断轮胎是否出现异常。这种方法能够实现实时采集的tda及fda跨速度区间的插值判断，解决了车辆的itpms系统在学习阶段无法完成所有主要速度区间的学习时导致的itpms系统不能在未学习的速度区间提供应有的报警功能的问题，有效解决了当前itpms系统存在的技术短板。
[0057]
2.本发明的基于速度区间插值的间接式胎压监测标定方法，通过对计算得到的拟合曲线进行误差分析，将拟合公式内的参数进行不断的更新，以得到最接近实际曲线的拟合曲线，保证插值计算公式的精准性。
附图说明
[0058]
图1是本发明的基于速度区间插值的间接式胎压监测标定方法的流程框图；
[0059]
图2是本发明的基于速度区间插值的间接式胎压监测标定方法的对tda与fda的标定值进行归一化处理前的分布示意图；
[0060]
图3是本发明的基于速度区间插值的间接式胎压监测标定方法的对tda与fda的标定值进行归一化处理后的分布示意图；
[0061]
图4是本发明的基于速度区间插值的间接式胎压监测标定方法的拟合曲线方程的曲线示意图；
具体实施方式
[0062]
为了使本发明的目的、技术方案和优点更加清楚，下面结合附图和具体实施例对本发明进行详细描述。
[0063]
在此，还需要说明的是，为了避免因不必要的细节而模糊了本发明，在附图中仅仅示出了与本发明的方案密切相关的结构和/或处理步骤，而省略了与本发明关系不大的其他细节。
[0064]
另外，还需要说明的是，术语“包括”、“包含”或者其任何其他变体意在涵盖非排他性的包含，从而使得包括一系列要素的过程、方法、物品或者设备不仅包括那些要素，而且还包括没有明确列出的其他要素，或者是还包括为这种过程、方法、物品或者设备所固有的要素。
[0065]
实施例
[0066]
如图1所示，一种基于速度区间插值的间接式胎压监测标定方法100，包括以下步骤：
[0067]
s1、车辆进入自学习阶段，itpms系统采集时域分析(time domain analysis，下文简称tda)和频域分析(frequency domain analysis，下文简称fda)的分析结果以作为原始标定值。
[0068]
在本步骤中，itpms系统在车辆自学习阶段所采集的tda与fda的原始标定值是分
速度区间来存储的。在车辆自学习完成之后，实时计算的tda和fda分析结果也是与相同速度区间的原始标定值进行比较。而本方法能够实现实时采集的tda及fda标定值的跨速度区间的插值判断。值得注意的是，该方法需要采集足够多的数据样本，以保证存在原始标定值的速度区间之间的间隔不会太大。基于此种情况，车辆自学习阶段是在平整光滑的路面上进行，且自学习阶段的时间不小于20min，以保证后续实时采样数据能满足插值条件。
[0069]
s2、将各个原始标定值对应的速度按数值大小划分成不同速度区间，并对各个速度区间内的tda与fda分别进行归一化处理。
[0070]
具体来讲，将样本点按对应速度大小进行归类，并以七个速度区间为例，将样本点划分成七个速度区间，并将各个速度区间内的tda与fda分别进行归一化处理：
[0071][0072]
式中，是修正后的标定值，v是原始值，μ是所有原始值的平均值，σ是所有原始值的标准差。
[0073]
随后，将tda与fda的标定值分别代入上式：
[0074][0075][0076][0077][0078][0079][0080]
式中：
[0081]
s表示速度区间，从1至7共有7个速度区间。
[0082]
表示在速度区间s内tda标定点的个数。
[0083]
表示在速度区间s中的每一个tda标定点的值，其中i是序号，取值在内。
[0084]
表示在速度区间s中的所有tda标定值的平均值。
[0085]
表示在速度区间s中的所有tda标定值的标准差。
[0086]
表示在速度区间s中经过归一化处理后的tda标定值，并分别与每一个相对应。
[0087]
表示在速度区间s内fda标定点的个数。
[0088]
表示在速度区间s中的每一个fda标定点的值，其中i是序号，取值在内。
[0089]
表示在速度区间s中的所有fda标定值的平均值。
[0090]
表示在速度区间si中的所有fda标定值的标准差。
[0091]
表示在速度区间si中经过归一化处理后的fda标定值，分别与每一个相对应。
[0092]
如图2所示，图中分布点为对tda与fda的标定值进行归一化处理前，tda与fda的标定值分布示意图。从图中可以看出，此时tda与fda的标定值呈离散型分布，相同速度区间内的tda与fda的标定值之间间隔较大，整体样本点波动较大，不利于后续分析。
[0093]
如图3所示，图中分布点为对tda与fda的标定值进行归一化处理后，tda与fda的标定值分布示意图。从图中可以看出，此时tda与fda的标定值分布较为紧凑，在相同速度区间内的tda与fda的标定值彼此重叠或接近，整体样本点平稳性好，后续分析结果更可靠。
[0094]
s3、将不同速度区间内的tda与fda标定值进行拟合，以得出不同速度区间内的tda及fda标定值之间的关系模型。
[0095]
具体来讲，步骤s3包括以下步骤：
[0096]
s31、将归一化后的tda与fda标定值采用梯度下降的方法进行多项式拟合，将速度区间作为自变量x，将速度区间对应的标定值作为因变量y来进行特征升维，升维后的结果如下：
[0097]
y＝θ0+θ1x+θ2x2+θ3x3+θ4x4+θ5x5+θ6x6+θ7x7[0098]
式中，x为每一个样本点对应的速度区间，y为每一个样本点对应的标定值，θ0至θ7为需要进行拟合的参数。该式用于反映速度区间与速度区间对应的标定值之间的关系模型，后续对该关系模型内的未知项进行分析，得出未知项后以将该关系模型补全。
[0099]
s32、采用随机数对参数θ0至θ7进行初始化，得到一组数组，并将该数组整合成参数矩阵：
[0100]
θ＝[θ
0 θ
1 θ
2 θ
3 θ
4 θ
5 θ
6 θ7]
[0101]
该参数矩阵可通过后续的计算进行求解，以得出参数θ的具体值。
[0102]
s33、将所有样本点的速度区间x整合成输入矩阵：
[0103][0104]
式中，m为所有样本点的个数；
[0105]
s34、将所有样本点的标定值整合成输出矩阵：
[0106]
y＝[y1ꢀ…ꢀ
y
m
]
[0107]
s35、将参数矩阵、输入矩阵以及输出矩阵带入拟合关系式，并采用梯度下降法求解θ：
[0108][0109]
将上式整合为：
[0110][0111]
该式为速度区间与速度区间对应的标定值之间的拟合曲线，该拟合曲线由于采用近似算法进行拟合，其关系模型与实际模型存在一定的偏差。为了保证该拟合曲线的准确
度，需要对该关系模型进行误差分析，以使拟合曲线最接近实际关系模型。
[0112]
s36、对s35中整合后的拟合公式进行误差分析，以得出最优化的拟合曲线。
[0113]
具体来讲，在步骤s36中，误差分析包括以下步骤：
[0114]
s361、对s35中整合后的公式的因变量进行误差预测，并定义损失函数：
[0115][0116]
式中，为拟合值与实际值之间的误差，以表示该拟合曲线所得到的速度区间的标定值与实际关系模型内的标定值的误差大小。
[0117]
s362、对参数矩阵θ进行梯度计算，以θ来对求偏导：
[0118][0119]
s363、对参数矩阵θ进行更新：
[0120]
θ＝θ
‑
αdθ
[0121]
式中，α为学习速率，并取值0.1。
[0122]
s364、重复步骤s363，以重复对θ进行更新，直至开始收敛，并将此时的参数矩阵θ记作由于当开始收敛时，θ为极值点，此时求得的值最接近实际数值，拟合效果最好。设此时的拟合曲线方程为：
[0123][0124]
如图4所示，该图为上式关系模型得到的拟合曲线。图中，曲线平滑过渡，极点分布均匀，拟合效果好。因此，上述拟合曲线方程的拟合效果好。
[0125]
s365、根据上述拟合曲线方程计算不同速度区间下标定值的差值，得出差值公式：
[0126]
δv
j
＝f(j+1)
‑
f(j)，j∈[1，6]。
[0127]
根据上述公式，可以将未学习的速度区间的样本点插入至其它学习过的速度区间内，并与该速度区间内的原始标定值比较，以判断当前轮胎的胎压状态，实现了实时采集的tda及fda的跨速度区间的插值判断。
[0128]
s4、判断行驶阶段车辆速度是否位于学习阶段的速度区间内，若是，将实时监测到的当前tda与fda直接与初始标定值比较后得出当前车胎的胎压状态，并判断是否报警；若不是，则执行s5。
[0129]
具体来讲，步骤s4包括以下步骤：
[0130]
s41、abs系统监测当前车辆行驶速度，并寻找其对应的速度区间；
[0131]
s42、读出步骤s41的速度区间内是否存在原始标定值；
[0132]
s43、若是，将实时监测到的当前tda与fda直接与原始标定值比较后判断是否报警；若不是，则执行s5。
[0133]
值得注意的是，由于该差值公式是根据原始标定值拟合出的关系曲线得到，速度区间相隔越近，其差值公式得到的关系模型越准确，速度区间相隔越远，其差值公式得到的关系模型误差越大。因而，当需要使用该公式时，需要满足相应的插值条件，才能保证该差值公式得出的结果最准确，保证胎压监测的精准度及可靠度。
[0134]
s5、判断当前tda与fda所属速度区间是否满足插值条件，若是，则将实时监测到的
当前tda与fda与插值后得到的速度区间的初始标定值比较后判断是否报警。
[0135]
具体来讲，在步骤s5中，插值条件包括部分速度区间在学习阶段采集到满足标定个数的原始标定值、以及不是跨超过两个的速度区间进行插值。
[0136]
具体分为下述三种情况：
[0137]
经过试验论证得知，当满足标定个数的原始标定值为单个速度区间的tda标定值个数大于25、以及fda标定值个数大于30。tda的标定值通常25秒左右会更新一个，所以在法规要求的20分钟自学习标定时间内最多会更新48个tda的标定值。但是，考虑到车辆在标定阶段会出现起停以及刹车等无效时间，所以设定当有35个tda标定值时自学习阶段完成。fda的标定速度比tda略快，在法规要求的20分钟自学习标定时间内最多会更新45个fda标定值。当tda标定值有25个，fda标定值有30个时，此时虽然二者均未标定完成，但样本点数量足够多，根据统计学规律此时的标定值已经有相当高的可靠性，与标定完成时的标定值相比差别不大，此时可以使用该速度区间的标定值对相邻的速度区间进行插值。
[0138]
在此条件下可将实测值插入至其速度区间的相邻两个速度区间内进行比较，此时根据差值公式得到的结果具备可靠性。
[0139]
根据此种情况，设满足标定个数要求的速度区间为速度区间
s
，则满足该插值条件的速度区间的标定值计算如下：
[0140]
当
s
＝1时，
[0141][0142]
当s＞1且s＜7时，
[0143][0144]
当s＝7时，
[0145][0146]
例如，将当前各个速度区间的标定值的个数用数组(n n y n n n n)表示，其中y表示该速度区间的标定值个数满足上述条件，n表示该速度区间的标定值个数不满足上述条件(下面所示的标记方法与该标记方法相同)。则能够进行采用差值公式进行插值预测的速度区间如数组(0 1 1 1 0 0 0)所示，其中1表示能采用差值公式进行插值预测，0表示不能采用差值公式进行插值预测(下面所示的标记方法与该标记方法相同)。
[0147]
当满足标定个数的原始标定值为两个速度区间的tda标定值个数大于10、以及fda标定值个数大于15，或者，两个速度区间的tda标定值个数之和大于30、以及fda标定值个数之和大于45。在此条件下可将实测值插入至其速度区间的相邻速度区间以及相隔一个速度区间的速度区间内进行比较，此时根据差值公式得到的结果具备可靠性。这种情形下要求两个满足条件的速度区间至多相隔一个速度区间，即二者要么相邻，要么间隔一个速度区间。
[0148]
在该情形中，以一个速度区间为相邻的速度区间的基准，这需要作为基准的速度区间的标定值足够可信。在当前情形中，是相邻两个速度区间互相做基准，所以此时单个速度区间的标定值个数可以少于情形一，但也要满足一定数量保证可靠性且两个速度区间总共的标定值个数要足够多。所以设置单个速度区间的tda标定值个数要大于10，fda标定值个数要大于15，两个速度区间总共的tda标定个数要大于30，fda标定值个数要大于45，在此条件下可以使用这两个速度区间的标定值对其他速度区间进行插值。
[0149]
例如，当两个速度区间相邻，则该相邻的两个速度区间能采用差值公式进行插值预测。将当前各个速度区间的标定值的个数用数组(n n n y y n n)表示，则能够进行采用差值公式进行插值预测的速度区间如数组(0 0 0 1 1 0 0)所示。
[0150]
根据此种情况，设满足标定个数要求的速度区间为速度区间s及速度区间s+1，则满足该插值条件的速度区间的标定值计算如下：
[0151][0152]
例如，当两个速度区间之间间隔一个速度区间，则该彼此之间间隔一个速度区间的两个速度区间能采用差值公式进行插值预测。将当前各个速度区间的标定值的个数用数组(n n n y n y n)表示，则能够进行采用差值公式进行插值预测的速度区间如数组(0 0 0 1 0 1 0)所示。
[0153]
根据此种情况，设满足标定个数要求的速度区间为速度区间s
‑
1及速度区间s+1，则满足该插值条件的速度区间的标定值计算如下：
[0154][0155]
值得注意的是，上述两种情况可以同时生效。
[0156]
当任意一个速度区间的tda标定值个数大于25且fda标定值个数大于30时，不再使用插值后的值作为当前速度区间的标定值，而是使用当前速度区间自身样本点计算出的值
作为标定值。这是由于插值算法是一种估计算法，且由于路况、车辆批次等因素会导致不同速度区间之间标定值的相关关系发生变化，这导致插值算法本身具有一定的系统误差，无法保证插值之后的分析结果一定准确，只能作为一种补充手段而无法替代真正的标定值，所以当某一速度区间的标定个数足够多时，应当首先使用其自身的标定值，而不是通过插值算法计算得到的标定值。
[0157]
通过上述方法的各个步骤，本发明通过将同一车辆的速度根据大小划分出不同的速度区间，并通过学习阶段的原始标定值拟合出各个速度区间之间的关系。从而根据车辆当前速度所属速度区间计算出可插入区间的标定值，并将计算的标定值与该速度区间的原始标定值作对比，从而判断轮胎是否出现异常。这种方法能够实现实时采集的tda及fda跨速度区间的插值判断，解决了车辆的itpms系统在学习阶段无法完成所有主要速度区间的学习时导致的itpms系统不能在未学习的速度区间提供应有的报警功能的问题，有效解决了当前itpms系统存在的技术短板。
[0158]
以上所述仅用以说明本发明的技术方案，而非对其进行限制；尽管参照前述实施例对本发明进行了详细的说明，本领域的普通技术人员应当理解：其依然可以对前述实施例所记载的技术方案进行修改，或者对其中部分或者全部技术特征进行等同替换；凡是利用本发明说明书及附图内容所作的等效结构或等效流程变换，或直接或间接运用在其他相关的技术领域，均同理包括在本发明的专利保护范围内。