一种车辆的横纵向综合控制方法及横纵向综合控制器

1.本发明涉及无人驾驶领域，特别是一种无人驾驶车辆(自动驾驶车辆)的横纵向综合控制方法及横纵向综合控制器。


背景技术：

2.自动驾驶已经成为学术界和汽车行业的热门研究领域。无人驾驶汽车的关键技术包括环境感知、决策、运动规划和路径跟踪。路径跟踪可以确保自动驾驶车辆采取适当的控制决策，沿着规划的路径行驶。在高速行驶时，这个问题更具有挑战性，因为车辆的稳定性和安全性是主要问题。
3.现有的自动驾驶车辆路径跟踪方法大多只考虑恒速下的车辆路径跟踪，路径曲率较小，且跟踪速度较慢。贺伊琳等人提出了一种优化型的滑模控制策略，并且将所提出的算法与传统的滑模控制进行对比，但是该方法完全忽略纵向的速度变化。基于自适应纯跟踪算法，myung-wook park等人提出了一种横向控制系统，该系统由路径跟踪器和原始驱动器组成，所提算法对纯跟踪算法进行了改进，原来的纯跟踪算法受到预瞄距离的影响较大，其会根据速度一直进行动态调整，为了解决该问题，作者应用了比例积分控制理论，结果显示所提出的算法在曲率较小路径上表现良好，但在曲率较大路径上结果与未改进的纯跟踪方法相似。
4.现有的自动驾驶车辆的控制决策主要包括横向控制、纵向控制。纵向控制是对车辆前进方向的速度控制，是指油门和刹车的协调，实现对变速的精确跟踪。横向控制是指转向控制，通常根据路径和曲率来减小跟踪误差。单独的横向控制或者纵向控制由于忽略了横纵向之间的强耦合关系，会导致跟踪的效果差。相比于解耦的横纵向跟踪控制，耦合后的横纵向跟踪控制不仅能够很大程度提升跟踪效果，并且车辆能够表现出良好的动力学性能，提升跟踪过程的舒适性同时减少车辆的能耗。
5.因此，本发明提出一种应用于无人驾驶领域且基于模型预测控制(mpc)理论设计的耦合后的横纵向跟踪控制方法及控制器是非常有必要的。


技术实现要素：

6.本发明的第一发明目的是：基于模型预测控制理论设计一种集成横向控制和纵向控制的综合控制方法，解决车辆在曲率较大的路径上跟踪效果不好的问题，并且提升车辆跟踪过程的舒适性同时减少车辆的能耗。
7.本发明实现其第一发明目所采取的技术方案是：
8.一种车辆的横纵向综合控制方法，包括以下步骤：
9.s1、获取当前场景中的路径信息，并规划出期望路径；所述路径信息包括路径上的每一点在惯性坐标系xoy(即大地坐标系)中x轴、y轴方向的坐标信息，路径的曲率信息，路面摩擦系数；
10.s2、将期望路径输入速度规划器和横向控制器；所述速度规划器是基于模型预测
控制理论及车辆运动学模型建立的；所述横向控制器是基于模型预测控制理论及车辆动力学模型建立的；
11.s3、速度规划器生成与期望路径相对应的关于车辆的期望速度曲线，得到并输出期望速度；
12.s4、横向控制器和纵向控制器分别接收速度规划器输出的期望速度；所述纵向控制器是基于模型预测控制理论设计的双层控制器，包括上层控制器和下层控制器；
13.s5、获取车辆状态信息并反馈给横向控制器和纵向控制器；所述车辆状态信息包括车辆在惯性坐标系xoy中的坐标、速度、航向角、航向角变化率；
14.s6、横向控制器和纵向控制器对接收的信息进行处理并输出，其中横向控制器的控制输出是车辆的前轮偏角，纵向控制器的控制输出是车辆的制动/油门(即加速度)；横向控制器和纵向控制器的控制输出同时给到车辆；(横向控制器接收速度规划器输出的期望速度，并结合期望路径和车辆状态信息计算出车辆的前轮偏角的增量(车轮转角)，并将所计算的车辆的前轮偏角的增量信号传递给车辆；纵向控制器接收速度规划器输出的期望速度，并结合车辆状态信息将接收的信息转换为期望制动压力/期望节气门开度信号传递给车辆。)
15.s7、车辆按照横向控制器和纵向控制器输出的控制信号进行相应操作；
16.s8、重复s3至s7，通过期望速度将横向控制器和纵向控制器耦合起来，综合控制车辆按照期望速度运行同时跟踪期望路径。
17.进一步地，所述速度规划器是基于模型预测控制理论及车辆运动学模型建立的，包括步骤：
18.sa-1、建立车辆运动学模型，并表示出车辆运动学模型的状态空间方程；
19.sa-2、运用前向欧拉方法对车辆运动学模型的状态空间进行离散化；
20.sa-3、基于离散化后的车辆运动学模型的状态空间，建立速度规划器的预测控制模型；
21.sa-4、由速度规划器的预测控制模型得到车辆的预测状态；
22.sa-5、基于车辆的预测状态，确定速度规划器的输出状态空间方程；
23.sa-6、基于车辆跟踪效果的考虑，建立关于期望路径的速度规划目标函数及预设约束条件，并建立速度规划器的输出约束条件；所述速度规划器的输出约束条件包括车辆的最大横向运动(所述车辆的最大横向运动包括车辆的最大横向加速度和最大横向偏移量，这里的“横向”是指垂直于车身的方向)和车辆的最大行驶速度。
24.进一步地，所述速度规划器是基于模型预测控制理论及车辆运动学模型建立的，具体包括步骤：
25.sa-1、建立车辆运动学模型(车辆运动学模型是基于简化的自行车模型建立的)：
[0026][0027]
由车辆运动学模型表示的状态空间方程如下：
[0028][0029]
上述中，x是车辆在惯性坐标系xoy中x轴方向的坐标，y是车辆在惯性坐标系xoy中
y轴方向的坐标，v是车辆的纵向速度(即：车辆沿车身方向的速度)，是车辆航向角(在速度规划中，把车辆看作一个质点，此时速度的方向跟航向角是相同的)，是车辆在惯性坐标系xoy下沿x轴方向的速度；是车辆在惯性坐标系xoy下沿y轴方向的速度，是车辆的纵向加速度(即：车辆沿车身方向的加速度)；是状态空间；s是状态量；u是控制量，这里是指加速度；a和b均是系数；
[0030]
sa-2、运用前向欧拉方法对车辆运动学模型的状态空间进行离散化，即：
[0031][0032][0033]
由此得到，离散化后的车辆运动学模型的状态空间：
[0034][0035]
上述中，s(k+1)是k+1时刻速度规划器的状态量；s(k)是k时刻速度规划器的状态量；t是离散的时间间隔；i是和a同阶的单位矩阵；是k时刻速度规划器的输出矩阵；u(k)是k时刻速度规划器的控制量，这里是指加速度；a(k)、b(k)和c(k)均是系数矩阵；
[0036]
sa-3、基于离散化后的车辆运动学模型的状态空间，建立速度规划器的预测控制模型，即：
[0037]
速度规划器的预测控制模型的状态空间方程中包含两个向量，一个是k时刻速度规划器的状态量s(k)，另一个是k-1时刻速度规划器的控制量u(k-1)；速度规划器的预测控制模型的状态空间方程为：
[0038][0039]
由离散化后的车辆运动学模型的状态空间，知：
[0040][0041]
由此建立速度规划器的预测控制模型为：
[0042][0043]
上述中，n
x
、nu分别是速度规划器的预测控制模型的状态向量和控制向量；i
nu
是nu*nu的单位矩阵；(i
nu
是单位矩阵，其中nu是控制量的维度)
[0044]
sa-4、基于速度规划器的预测控制模型进行车辆的预测状态推导，结果如下：
[0045][0046]
其中，nc是速度规划器控制时域，n
p
是速度规划器预测时域，且n
p
＞nc；
[0047]
sa-5、基于推导出的车辆的预测状态，确定速度规划器的输出状态空间方程：
[0048][0049]
所述速度规划器的输出状态空间方程可以简化为如下矩阵：
[0050][0051]
其中，δu(k)＝[δu(k)δu(k+1)...δu(k+nc)]
t
；
[0052]
sa-6、基于车辆跟踪效果的考虑，建立关于期望路径的速度规划目标函数及预设约束条件，并建立速度规划器的输出约束条件；所述速度规划器的输出约束条件包括车辆的最大横向运动和车辆的最大行驶速度；具体包括：
[0053]
sa-6-1、建立关于期望路径的速度规划目标函数如下：
[0054][0055]
式(12)中，用于衡量车辆行驶的平稳性，用于衡
量车辆跟踪的舒适性，用于衡量车辆的跟踪效率，用于衡量车辆的跟踪误差；其中，a(k+i)是从k时刻开始到速度规划器控制时域内每一个时刻的加速度；j(k+i)是从k时刻开始到速度规划器控制时域内每一个时刻的加加速度(加加速度是加速度对时间的导数，衡量加速度的变化率)；v(k+i)是从k时刻开始到速度规划器预测时域内每一个时刻车辆的实际速度；v
ref
(k+i)是从k时刻开始到速度规划器预测时域内每一个时刻的参考速度；是从k时刻开始到速度规划器预测时域内每一个时刻车辆的实际输出量；是从k时刻开始到速度规划器预测时域内每一个时刻的输出量参考值；nc是速度规划器控制时域，n
p
是速度规划器预测时域，且n
p
＞nc；r1是车辆加速度的惩罚矩阵，r2是车辆加加速度的惩罚矩阵，q1是车辆速度的惩罚矩阵，q2是车辆跟踪效果的惩罚矩阵，并且r1、r2、q1和q2这四个惩罚矩阵均是正定矩阵(为了保证解是凸解)；
[0056]
sa-6-2、建立关于期望路径的预设约束条件如下：
[0057]umin
≤u(k+i)≤u
max
，i＝0，1，2，
…
，n
c-1；
ꢀꢀꢀ
(13)
[0058]
δu
min
≤δu(k+i)≤δu
max
，i＝0，1，2，
…
，n
c-1；
ꢀꢀꢀ
(14)
[0059]
式(13)是对速度规划器控制量的约束，u
min
是速度规划器控制量的最小约束值，u
max
是速度规划器控制量的最大约束值；式(14)是对速度规划器控制量增量的约束，δu
mi
n是速度规划器控制量增量的最小约束值，δu
max
是速度规划器控制量增量的最大约束值；
[0060]
sa-6-3、建立速度规划器的输出约束条件如下：
[0061]
η
min
≤η(k+i)≤η
max
，i＝0，1，2，
…
，n
p-1；
ꢀꢀꢀ
(15)
[0062]
式(15)中，η
min
是速度规划器的输出最小约束值，η
max
是速度规划器的输出最大约束值；
[0063]
sa-6-4、确定车辆的约束速度最大值如下：
[0064]vref
＝vm＝min(vr，vc)；
ꢀꢀꢀ
(16)
[0065]
式(16)中，vr是路径的最高限速，vc是根据路径信息及车身信息计算路径几何参数给车辆的限速；v
ref
是参考速度；vm是最大速度。
[0066]
进一步地，所述根据路径信息及车身信息计算路径几何参数给车辆的限速vc，具体为：
[0067][0068]
式(17)中，d是车辆后轮的轴距；h是车辆重心距离地面的高度；g是重力加速度；r是车辆的转弯半径，其中ρ是路径曲率，满足其中ρ是路径曲率，满足是在惯性坐标系xoy下沿x轴方向的路径表达式对时间的一阶导数，是在惯性坐标系xoy下沿y轴方向的路径表达式对时间的一阶导数，是在惯性坐标系xoy下沿x轴方向的路径表达式对时间的二阶导数，是在惯性坐标系xoy下沿y轴方向的路径表达式对时间的二阶导数。
[0069]
进一步地，所述横向控制器是基于模型预测控制理论及车辆动力学模型建立的，
包括步骤：(由于车辆复杂度高并且车辆横纵向之间存在强耦合，所以为了提升车辆的跟踪效果，需要考虑轮胎力及其他更复杂的受力情况。)
[0070]
sb-1、建立车辆动力学模型，包括：
[0071]
在车身坐标系xoy下，车辆质心沿x轴方向的动力学方程为：
[0072]
车辆质心沿y轴方向的动力学方程为：
[0073]
车辆质心沿z轴方向的动力学方程为：
[0074]
上述中，m是整车质量，是车辆的横向速度(即：车辆沿垂直于车身方向的速度)，是车辆的纵向速度(即：车辆沿车身方向的速度)，是车辆的横向加速度(即：车辆沿垂直于车身方向的加速度)，是车辆的纵向加速度(即：车辆沿车身方向的加速度)，是车辆航向角，是车辆航向角对时间的一阶导数，是车辆航向角对时间的二阶导数，f
xf
是车辆前轮受到在车身坐标系xoy下沿x轴方向的力，f
xr
是车辆后轮受到在车身坐标系xoy下沿x轴方向的力，f
yf
是车辆前轮受到在车身坐标系xoy下沿y轴方向的力，f
yr
是车辆后轮受到在车身坐标系xoy下沿y轴方向的力，z是车辆的转动惯量，b1是车辆质心到其前轴的距离，b2是车辆质心到其后轴的距离；
[0075]
考虑车身坐标系xoy与惯性坐标系xoy之间的关系，可得：
[0076][0077][0078]
上述中，是车辆在惯性坐标系xoy下沿x轴方向的速度，是车辆在惯性坐标系xoy下沿y轴方向的速度，是车辆在车身坐标系xoy下沿x轴方向的速度，是车辆在车身坐标系xoy下沿y轴方向的速度，是车辆航向角；
[0079]
车辆前、后轮在车身坐标系xoy下沿x轴方向和y轴方向受到的合力与车辆前、后轮受到的纵向力、侧向力的转换如下：
[0080]fyf
＝f
lf sin δf+f
cf cos δf，
ꢀꢀꢀ
(23)
[0081]fyr
＝f
lr sin δr+f
cr cos δr，
ꢀꢀꢀ
(24)
[0082]fxf
＝f
lf cos δ
f-f
cf sin δf，
ꢀꢀꢀ
(25)
[0083]fxr
＝f
lr cos δ
r-f
cr sin δr；
ꢀꢀꢀ
(26)
[0084]
上述中，f
xf
是车辆前轮受到在车身坐标系xoy下沿x轴方向的力，f
xr
是车辆后轮受到在车身坐标系xoy下沿x轴方向的力，f
yf
是车辆前轮受到在车身坐标系xoy下沿y轴方向的力，f
yr
是车辆后轮受到在车身坐标系xoy下沿y轴方向的力，f
cr
是车辆前轮受到的侧向力(即：车辆前轮受到沿垂直于车辆前轮行进方向的力)，f
cr
是车辆后轮受到的侧向力(即：车辆后轮受到沿垂直于车辆后轮行进方向的力)，f
lf
是车辆前轮受到的纵向力(即：车辆前轮受到沿车辆前轮行进方向的力)，f
lr
是车辆后轮受到的纵向力(即：车辆后轮受到沿车辆后
轮行进方向的力)，δf是车辆的前轮偏角(即：在车身坐标系xoy下，车辆前轮行进方向与x轴方向的夹角)，δr是车辆的后轮偏角，且δr＝0(即：在车身坐标系xoy下，车辆后轮行进方向与x轴方向的夹角；由于本发明专注于前轮主动转向，所以此处δr＝0)；
[0085]
由于轮胎的纵向力和侧向力均与滑移角、滑移率、路面摩擦系数、轮胎的垂直载荷相关，故轮胎的纵向力和侧向力可以表示为如下形式：
[0086][0087][0088]
滑移率定义为：
[0089]
上述中，f
l
是轮胎的纵向力(即：轮胎受到沿轮胎行进方向的力)，fc是轮胎的侧向力(即：轮胎受到沿垂直于轮胎行进方向的力)，α是滑移角，是滑移率，μ是路面摩擦系数，fz是轮胎的垂直载荷(即：轮胎受到沿垂直于路面方向的力)，v
l
是轮胎的纵向速度(即：轮胎沿其自身行进方向上的速度)，r是轮胎半径，ω是角速度；
[0090]
所述滑移角为：
[0091]
其中，轮胎的侧向速度为：vc＝v
y cos δ-v
x sin δ，
ꢀꢀꢀ
(31)
[0092]
轮胎的纵向速度为：v
l
＝v
y sin δ-v
x cos δ，
ꢀꢀꢀ
(32)
[0093]
且v
x
、vy分别是vc和v
l
在车身坐标系xoy下沿x轴方向、y轴方向的合速度，δ是车轮偏角；
[0094]
(补充说明：公式(27)至公式(32)为广义公式，同时适用于车辆前轮与车辆后轮的轮胎分析。)
[0095]
在车身坐标系xoy下，车辆前、后轮在x轴方向、y轴方向的速度可通过如下式子进行转换：
[0096][0097][0098][0099][0100]
上述中，v
yf
是车辆前轮在车身坐标系xoy下沿y轴方向的速度，v
yr
是车辆后轮在车身坐标系xoy下沿y轴方向的速度，v
xf
是车辆前轮在车身坐标系xoy下沿x轴方向的速度，v
xr
是车辆后轮在车身坐标系xoy下沿x轴方向的速度，是车辆在车身坐标系xoy下沿x轴方向的速度，是车辆在车身坐标系xoy下沿y轴方向的速度，是车辆航向角对时间的一阶导数，b1是车辆质心到其前轴的距离，b2是车辆质心到其后轴的距离；
[0101]
假设车辆前、后轴的载荷转移忽略不计，则：
[0102]
车辆前轮所受到的垂向载荷为：
[0103]
车辆后轮所受到的垂向载荷为：
[0104]
上述中，b1是车辆质心到其前轴的距离，b2是车辆质心到其后轴的距离，m是整车质量，g是重力加速度(这些参数都可以根据车辆的状态信息进行计算得到；在实际控制过程中，假设滑移率和路面摩擦系数μ是已知的)；
[0105]
由此得到，非线性车辆动力学微分方程为：
[0106]
其中，ζ(t)是t时刻横向控制器的状态量，其中，ζ(t)是t时刻横向控制器的状态量，是t时刻的横向控制器的控制量，横向控制器的控制量，是车辆在车身坐标系xoy下沿x轴方向的速度，是车辆在车身坐标系xoy下沿y轴方向的速度；是车辆航向角，是车辆航向角对时间的一阶导数；x是车辆在惯性坐标系xoy中x轴方向的坐标，y是车辆在惯性坐标系xoy中y轴方向的坐标；δf是车辆的前轮偏角；
[0107]
sb-2、基于非线性车辆动力学微分方程和模型预测控制理论，建立横向控制器的状态空间方程，及其目标函数和约束条件：
[0108][0109][0110][0111]
上述中，公式(40)是在离散时间模型下的表达式；是t时刻横向控制器的控制量，量，是t-1时刻横向控制器的控制量；是横向控制器控制量的增量，ζ(t)是t时刻横向控制器的状态量；ζ(t+1)是t+1时刻横向控制器的状态量；δf是车辆的前轮偏角，δδf是车辆前轮偏角的增量；是t时刻横向控制器的输出，是与横向控制器状态量对应的输出矩阵；
[0112]
考虑车辆在跟踪过程中的准确性、稳定性及舒适性所得横向控制器的目标函数如下：
[0113][0114]
上式中，是在t时刻求得的横向控制器的最优控制量，是t时刻求出的不同横向控制器控制时域内的最优控制量的增量序列，下标代表的是不同时刻；h
p
是横向控制器预测时域；hc是横向控制器控制时域；ε是松弛因子；为t时刻预测的t+i时刻横向控制器的控制输出；是t时刻预测的t+i时刻横向控制器的状态量(状态量即为系统的输出量)参考值；是t时刻预测的t+
i时刻横向控制器控制量的增量；是t时刻预测的t+i时刻横向控制器的控制量；是权重系数；q是横向控制器状态量的权重矩阵；g是横向控制器控制量增量的权重矩阵；s是横向控制器控制量的权重矩阵；
[0115]
为了对横向控制器的整个控制过程进行优化，在每一时刻均对以下优化模型进行求解：(求解该优化模型实际就是求解每一时刻的横向控制器控制量的增量，即：在每一个时刻都需要求出横向控制器控制时域内的控制量的增量序列，从而求出横向控制器控制量，对系统进行控制。)
[0116][0117]
关于车辆动力学方面的约束条件：
[0118][0119][0120][0121]
ζ
t，t
＝ζ(t)；
ꢀꢀꢀ
(48)
[0122][0123][0124]
关于车辆的前轮偏角的约束条件：
[0125][0126]
关于车辆的前轮偏角增量的约束条件：
[0127][0128]
上述中，ζ
k+1，t
是t时刻预测的k+1时刻横向控制器的状态量，是车辆动力学模型表达式，ζ
k，t
是t时刻预测的k时刻横向控制器的状态量，是t时刻预测的k时刻横向控制器的控制量，是t时刻预测的k-1时刻横向控制器的控制量，是t时刻得到的k时刻横向控制器控制量的增量，是t时刻预测的k时刻横向控制器的输出，h
2ω
(ζ
k，t
)是车辆动力学相关约束(在简化的车辆二轮模型下与车辆状态量相关的动力学约束)，ω是角速度，ζ
t，t
是t时刻横向控制器的状态量，ζ(t)是t时刻横向控制器的状态量，是t时刻预测的t-1时刻横向控制器的控制量，是t-1时刻横向控制器的控制量，是t时刻横向控制器的控制量，是t时刻横向控制器的控制量，是横向控制器控制量的下限，是横向控制器控制量的上限，是横向控制器控制量增量的下限，是横向控制器控制量增量的上限。
[0129]
进一步地，所述纵向控制器是基于模型预测控制理论设计的双层控制器，包括上层控制器和下层控制器；所述上层控制器根据期望速度及车辆状态信息计算出期望加速度，并将计算出的期望加速度传递给下层控制器；所述下层控制器将接收到的期望加速度同当前空气阻力和滚动阻力的大小与车辆质量的比值进行比较，然后根据切换逻辑判断车
辆应当进行加速操作还是制动操作，将节气门开度值/制动压力值传给车辆，车辆进行相应操作后再将控制结果反馈给上层控制器，形成闭环控制。
[0130]
本发明的第二发明目的是：基于模型预测控制理论设计一种集成横向控制和纵向控制的综合控制器，解决车辆在曲率较大的路径上跟踪效果不好的问题，并且提升车辆跟踪过程的舒适性同时减少车辆的能耗。
[0131]
本发明实现其第二发明目所采取的技术方案是：
[0132]
一种车辆的横纵向综合控制器，所述车辆的横纵向综合控制器是采用所述的车辆的横纵向综合控制方法进行的；
[0133]
所述车辆的横纵向综合控制器包括速度规划器、横向控制器和纵向控制器；
[0134]
所述速度规划器是基于模型预测控制理论及车辆运动学模型建立的，用于生成与期望路径相对应的关于车辆的期望速度曲线，得到并输出期望速度；
[0135]
所述横向控制器是基于模型预测控制理论及车辆动力学模型建立的；所述横向控制器接收所述速度规划器输出的期望速度，结合期望路径和车辆状态信息计算出车辆的前轮偏角的增量，并将所计算的车辆的前轮偏角的增量信号传递给车辆，即所述横向控制器的控制输出是车辆的前轮偏角；
[0136]
所述纵向控制器是基于模型预测控制理论设计的双层控制器，包括上层控制器和下层控制器；所述纵向控制器接收所述速度规划器输出的期望速度，并结合车辆状态信息将接收的信息转换为期望制动压力/期望节气门开度信号传递给车辆，即所述纵向控制器的控制输出是车辆的制动/油门；
[0137]
所述纵向控制器的控制过程具体包括：所述上层控制器根据期望速度及车辆状态信息计算出期望加速度，并将计算出的期望加速度传递给下层控制器；所述下层控制器将接收到的期望加速度同当前空气阻力和滚动阻力的大小与车辆质量的比值进行比较，然后根据切换逻辑判断车辆应当进行加速操作还是制动操作，将节气门开度值/制动压力值传给车辆，车辆进行相应操作后再将控制结果反馈给上层控制器，形成闭环控制；
[0138]
所述横向控制器和所述纵向控制器的控制输出将同时给到车辆，车辆依据接收到的控制信号做出相应操作，并且将车辆状态信息反馈给横向控制器和纵向控制器；
[0139]
所述横向控制器和所述纵向控制器是通过期望速度耦合起来的，由此综合控制车辆按照期望速度运行同时跟踪期望路径。
[0140]
与现有技术相比，本发明方法的有益效果是：
[0141]
(1)本发明方法首先针对曲率较大的已知路径规划出期望路径，然后将期望路径输入运用模型预测控制理论设计横向控制器和纵向控制器。纵向控制器是对车辆前进方向的速度控制，即对油门和刹车的协调控制，实现对期望速度的跟踪；横向控制器是对车辆前轮偏转角的控制，减小车辆实际行驶路径与期望路径的跟踪误差。本发明方法集成横向控制和纵向控制的优势，通过期望速度将横向控制器和纵向控制器耦合起来，使车辆在跟踪期望路径的时候以期望速度进行变速跟踪，同时尽量贴合所跟踪的期望路径。本发明方法考虑车辆横向和纵向的运动，同时考虑二者的相互影响，使得车辆在尽可能跟踪期望路径的同时跟踪期望速度，这样不仅能够提升跟踪效率，同时跟踪效果也会极大提升，而且在横向控制器中运用的是车辆动力学模型，相比车辆的运动学模型，能够体现出更好的车辆动力学性能。
[0142]
(2)本发明的横纵向综合控制器是基于模型预测控制设计的集成了横向控制和纵向控制的优势的综合控制器，其中纵向控制器是对车辆前进方向的速度控制，即对油门和刹车的协调控制，实现对期望速度的跟踪；横向控制器是对车辆前轮偏转角的控制，减小车辆实际行驶路径与期望路径的跟踪误差；该横纵向综合控制器是通过期望速度将横向控制器和纵向控制器耦合起来的。采用本发明的横纵向综合控制器对车辆进行控制，车辆能够在跟踪期望路径的时候以期望速度进行变速跟踪，同时能够尽可能地贴合所跟踪的期望路径。本发明的横纵向综合控制器不仅考虑了车辆的横向跟踪误差，还对车辆速度进行控制，能够极大程度提升车辆的跟踪效率和跟踪效果，同时降低能耗，提升跟踪舒适性。
[0143]
(3)本发明车辆的横纵向综合控制方法及横纵向综合控制器采用速度规划器对车辆速度进行规划，其优势是：该速度规划器是基于模型预测控制理论进行速度规划，能够对车辆前方的路径情况进行预测，提前获取路径信息，从而在弯道之前就能够使车辆提前减速，缓慢过弯，过弯后由于车辆又提前获取到前方的直道信息，能够在过弯后及时加速，以较快的速度在直道上行驶。因此，采用本发明，车辆不会出现急加速急减速的情况，提升了整个跟踪过程的舒适性；而在直道上又以较大速度行驶，提升了跟踪效率，同时也减少了能耗。这不仅使车辆极好地适应了大曲率路径以及不规则路径，还提升了被控驾驶车辆的舒适性与安全性。
[0144]
下面通过具体实施方式及附图对本发明作进一步详细说明，但并不意味着对本发明保护范围的限制。
附图说明
[0145]
图1是本发明实施例的车辆运动学模型示意图。
[0146]
图2是本发明实施例参考路径示意图。
[0147]
图3是本发明实施例规划出的期望路径和生成的期望速度曲线图。
[0148]
图4是本发明实施例速度控制序列图。
[0149]
图5是本发明实施例加速度控制序列图。
[0150]
图6是本发明实施例车辆动力学模型示意图。
[0151]
图7是本发明实施例魔术轮胎公式。
[0152]
图8是本发明实施例横向控制器在单独控制时的控制示意图。
[0153]
图9是本发明实施例纵向控制器在单独控制时的控制示意图。
[0154]
图10是本发明实施例车辆的横纵向综合控制器的控制示意图。
具体实施方式
[0155]
下面结合附图，通过对实施例的描述，对本发明的具体实施方式作进一步的说明。
[0156]
实施例
[0157]
本例给出了一种车辆的横纵向综合控制方法，包括以下步骤：
[0158]
s1、获取当前场景中的路径信息，并规划出期望路径；所述路径信息包括路径上的每一点在惯性坐标系xoy(即大地坐标系)中x轴、y轴方向的坐标信息，路径的曲率信息，路面摩擦系数；
[0159]
s2、将期望路径输入速度规划器和横向控制器；所述速度规划器是基于模型预测
控制理论及车辆运动学模型建立的；所述横向控制器是基于模型预测控制理论及车辆动力学模型建立的；
[0160]
s3、速度规划器生成与期望路径相对应的关于车辆的期望速度曲线，得到并输出期望速度；
[0161]
s4、横向控制器和纵向控制器分别接收速度规划器输出的期望速度；所述纵向控制器是基于模型预测控制理论设计的双层控制器，包括上层控制器和下层控制器；
[0162]
s5、获取车辆状态信息并反馈给横向控制器和纵向控制器；所述车辆状态信息包括车辆在惯性坐标系xoy中的坐标、速度、航向角、航向角变化率；
[0163]
s6、横向控制器和纵向控制器对接收的信息进行处理并输出，其中横向控制器的控制输出是车辆的前轮偏角，纵向控制器的控制输出是车辆的制动/油门(即加速度)；横向控制器和纵向控制器的控制输出同时给到车辆；(横向控制器接收速度规划器输出的期望速度，并结合期望路径和车辆状态信息计算出车辆的前轮偏角的增量(车轮转角)，并将所计算的车辆的前轮偏角的增量信号传递给车辆；纵向控制器接收速度规划器输出的期望速度，并结合车辆状态信息将接收的信息转换为期望制动压力/期望节气门开度信号传递给车辆。)
[0164]
s7、车辆按照横向控制器和纵向控制器输出的控制信号进行相应操作；
[0165]
s8、重复s3至s7，通过期望速度将横向控制器和纵向控制器耦合起来，综合控制车辆按照期望速度运行同时跟踪期望路径。
[0166]
本例中，所述速度规划器是基于模型预测控制理论及车辆运动学模型建立的，包括步骤：
[0167]
sa-1、建立车辆运动学模型，并表示出车辆运动学模型的状态空间方程；
[0168]
sa-2、运用前向欧拉方法对车辆运动学模型的状态空间进行离散化；
[0169]
sa-3、基于离散化后的车辆运动学模型的状态空间，建立速度规划器的预测控制模型；
[0170]
sa-4、由速度规划器的预测控制模型得到车辆的预测状态；
[0171]
sa-5、基于车辆的预测状态，确定速度规划器的输出状态空间方程；
[0172]
sa-6、基于车辆跟踪效果的考虑，建立关于期望路径的速度规划目标函数及预设约束条件，并建立速度规划器的输出约束条件；所述速度规划器的输出约束条件包括车辆的最大横向运动(所述车辆的最大横向运动包括车辆的最大横向加速度和最大横向偏移量，这里的“横向”是指垂直于车身的方向)和车辆的最大行驶速度。
[0173]
本例中，所述速度规划器是基于模型预测控制理论及车辆运动学模型建立的，具体包括步骤：
[0174]
sa-1、建立车辆运动学模型(车辆运动学模型是基于简化的自行车模型建立的)：
[0175][0176]
由车辆运动学模型表示的状态空间方程如下：
[0177][0178]
上述中，x是车辆在惯性坐标系xoy中x轴方向的坐标，y是车辆在惯性坐标系xoy中
y轴方向的坐标，v是车辆的纵向速度(即：车辆沿车身方向的速度)，是车辆航向角(在速度规划中，把车辆看作一个质点，此时速度的方向跟航向角是相同的)，是车辆在惯性坐标系xoy下沿x轴方向的速度；是车辆在惯性坐标系xoy下沿y轴方向的速度，是车辆的纵向加速度(即：车辆沿车身方向的加速度)；是状态空间；s是状态量；u是控制量，这里是指加速度；a和b均是系数；
[0179]
sa-2、运用前向欧拉方法对车辆运动学模型的状态空间进行离散化，即：
[0180][0181][0182]
由此得到，离散化后的车辆运动学模型的状态空间：
[0183][0184]
上述中，s(k+1)是k+1时刻速度规划器的状态量；s(k)是k时刻速度规划器的状态量；t是离散的时间间隔；i是和a同阶的单位矩阵；是k时刻速度规划器的输出矩阵；u(k)是k时刻速度规划器的控制量，这里是指加速度；a(k)、b(k)和c(k)均是系数矩阵；
[0185]
sa-3、基于离散化后的车辆运动学模型的状态空间，建立速度规划器的预测控制模型，即：
[0186]
速度规划器的预测控制模型的状态空间方程中包含两个向量，一个是k时刻速度规划器的状态量s(k)，另一个是k-1时刻速度规划器的控制量u(k-1)；速度规划器的预测控制模型的状态空间方程为：
[0187][0188]
由离散化后的车辆运动学模型的状态空间，知：
[0189][0190]
由此建立速度规划器的预测控制模型为：
[0191][0192]
上述中，n
x
、nu分别是速度规划器的预测控制模型的状态向量和控制向量；i
nu
是nu*nu的单位矩阵；(i
nu
是单位矩阵，其中nu是控制量的维度)
[0193]
sa-4、基于速度规划器的预测控制模型进行车辆的预测状态推导，结果如下：
[0194][0195]
其中，nc是速度规划器控制时域，n
p
是速度规划器预测时域，且n
p
＞nc；
[0196]
sa-5、基于推导出的车辆的预测状态，确定速度规划器的输出状态空间方程：
[0197][0198]
所述速度规划器的输出状态空间方程可以简化为如下矩阵：
[0199][0200]
其中，δu(k)＝[δu(k)δu(k+1)...δu(k+nc)]
t
；
[0201]
sa-6、基于车辆跟踪效果的考虑，建立关于期望路径的速度规划目标函数及预设约束条件，并建立速度规划器的输出约束条件；所述速度规划器的输出约束条件包括车辆的最大横向运动和车辆的最大行驶速度；具体包括：
[0202]
sa-6-1、建立关于期望路径的速度规划目标函数如下：
[0203][0204]
式(12)中，用于衡量车辆行驶的平稳性，用于衡
量车辆跟踪的舒适性，用于衡量车辆的跟踪效率，用于衡量车辆的跟踪误差；其中，a(k+i)是从k时刻开始到速度规划器控制时域内每一个时刻的加速度；j(k+i)是从k时刻开始到速度规划器控制时域内每一个时刻的加加速度(加加速度是加速度对时间的导数，衡量加速度的变化率)；v(k+i)是从k时刻开始到速度规划器预测时域内每一个时刻车辆的实际速度；v
ref
(k+i)是从k时刻开始到速度规划器预测时域内每一个时刻的参考速度；是从k时刻开始到速度规划器预测时域内每一个时刻车辆的实际输出量；是从k时刻开始到速度规划器预测时域内每一个时刻的输出量参考值；nc是速度规划器控制时域，n
p
是速度规划器预测时域，且n
p
＞nc；r1是车辆加速度的惩罚矩阵，r2是车辆加加速度的惩罚矩阵，q1是车辆速度的惩罚矩阵，q2是车辆跟踪效果的惩罚矩阵，并且r1、r2、q1和q2这四个惩罚矩阵均是正定矩阵(为了保证解是凸解)；
[0205]
sa-6-2、建立关于期望路径的预设约束条件如下：
[0206]umin
≤u(k+i)≤u
max
，i＝0，1，2，
…
，n
c-1；
ꢀꢀꢀ
(13)
[0207]
δu
min
≤δu(k+i)≤δu
max
，i＝0，1，2，
…
，n
c-1；
ꢀꢀꢀ
(14)
[0208]
式(13)是对速度规划器控制量的约束，u
min
是速度规划器控制量的最小约束值，u
max
是速度规划器控制量的最大约束值；式(14)是对速度规划器控制量增量的约束，δu
min
是速度规划器控制量增量的最小约束值，δu
max
是速度规划器控制量增量的最大约束值；
[0209]
sa-6-3、建立速度规划器的输出约束条件如下：
[0210]
η
min
≤η(k+i)≤η
max
，i＝0，1，2，
…
，n
p-1；
ꢀꢀꢀ
(15)
[0211]
式(15)中，η
min
是速度规划器的输出最小约束值，η
max
是速度规划器的输出最大约束值；
[0212]
sa-6-4、确定车辆的约束速度最大值如下：
[0213]vref
＝vm＝min(vr，vc)；
ꢀꢀꢀ
(16)
[0214]
式(16)中，vr是路径的最高限速，vc是根据路径信息及车身信息计算路径几何参数给车辆的限速；v
ref
是参考速度；vm是最大速度。
[0215]
本例中，所述根据路径信息及车身信息计算路径几何参数给车辆的限速vc，具体为：
[0216][0217]
式(17)中，d是车辆后轮的轴距；h是车辆重心距离地面的高度；g是重力加速度；r是车辆的转弯半径，其中ρ是路径曲率，满足其中ρ是路径曲率，满足是在惯性坐标系xoy下沿x轴方向的路径表达式对时间的一阶导数，是在惯性坐标系xoy下沿y轴方向的路径表达式对时间的一阶导数，是在惯性坐标系xoy下沿x轴方向的路径表达式对时间的二阶导数，是在惯性坐标系xoy下沿y轴方向的路径表达式对时间的二阶导数。
[0218]
本例中，所述横向控制器是基于模型预测控制理论及车辆动力学模型建立的，包
括步骤：(由于车辆复杂度高并且车辆横纵向之间存在强耦合，所以为了提升车辆的跟踪效果，需要考虑轮胎力及其他更复杂的受力情况。)
[0219]
sb-1、建立车辆动力学模型，包括：
[0220]
在车身坐标系xoy下，车辆质心沿x轴方向的动力学方程为：
[0221]
车辆质心沿y轴方向的动力学方程为：
[0222]
车辆质心沿z轴方向的动力学方程为：
[0223]
上述中，m是整车质量，是车辆的横向速度(即：车辆沿垂直于车身方向的速度)，是车辆的纵向速度(即：车辆沿车身方向的速度)，是车辆的横向加速度(即：车辆沿垂直于车身方向的加速度)，是车辆的纵向加速度(即：车辆沿车身方向的加速度)，是车辆航向角，是车辆航向角对时间的一阶导数，是车辆航向角对时间的二阶导数，f
xf
是车辆前轮受到在车身坐标系xoy下沿x轴方向的力，f
xr
是车辆后轮受到在车身坐标系xoy下沿x轴方向的力，f
yf
是车辆前轮受到在车身坐标系xoy下沿y轴方向的力，f
yr
是车辆后轮受到在车身坐标系xoy下沿y轴方向的力，z是车辆的转动惯量，b1是车辆质心到其前轴的距离，b2是车辆质心到其后轴的距离；
[0224]
考虑车身坐标系xoy与惯性坐标系xoy之间的关系，可得：
[0225][0226][0227]
上述中，是车辆在惯性坐标系xoy下沿x轴方向的速度，是车辆在惯性坐标系xoy下沿y轴方向的速度，是车辆在车身坐标系xoy下沿x轴方向的速度，是车辆在车身坐标系xoy下沿y轴方向的速度，是车辆航向角；
[0228]
车辆前、后轮在车身坐标系xoy下沿x轴方向和y轴方向受到的合力与车辆前、后轮受到的纵向力、侧向力的转换如下：
[0229]fyf
＝f
lf sin δf+f
cf cos δf，
ꢀꢀꢀ
(23)
[0230]fyr
＝f
lr sin δr+f
cr cos δr，
ꢀꢀꢀ
(24)
[0231]fxf
＝f
lf cos δ
f-f
cf sin δf，
ꢀꢀꢀ
(25)
[0232]fxr
＝f
lr cos δ
r-f
cr sin δr；
ꢀꢀꢀ
(26)
[0233]
上述中，f
xf
是车辆前轮受到在车身坐标系xoy下沿x轴方向的力，f
xr
是车辆后轮受到在车身坐标系xoy下沿x轴方向的力，f
yf
是车辆前轮受到在车身坐标系xoy下沿y轴方向的力，f
yr
是车辆后轮受到在车身坐标系xoy下沿y轴方向的力，f
cf
是车辆前轮受到的侧向力(即：车辆前轮受到沿垂直于车辆前轮行进方向的力)，f
cr
是车辆后轮受到的侧向力(即：车辆后轮受到沿垂直于车辆后轮行进方向的力)，f
lf
是车辆前轮受到的纵向力(即：车辆前轮受到沿车辆前轮行进方向的力)，f
lr
是车辆后轮受到的纵向力(即：车辆后轮受到沿车辆后
轮行进方向的力)，δf是车辆的前轮偏角(即：在车身坐标系xoy下，车辆前轮行进方向与x轴方向的夹角)，δr是车辆的后轮偏角，且δr＝0(即：在车身坐标系xoy下，车辆后轮行进方向与x轴方向的夹角；由于本发明专注于前轮主动转向，所以此处δr＝0)；
[0234]
由于轮胎的纵向力和侧向力均与滑移角、滑移率、路面摩擦系数、轮胎的垂直载荷相关，故轮胎的纵向力和侧向力可以表示为如下形式：
[0235][0236][0237]
滑移率定义为：
[0238]
上述中，f
l
是轮胎的纵向力(即：轮胎受到沿轮胎行进方向的力)，fc是轮胎的侧向力(即：轮胎受到沿垂直于轮胎行进方向的力)，α是滑移角，是滑移率，μ是路面摩擦系数，fz是轮胎的垂直载荷(即：轮胎受到沿垂直于路面方向的力)，v
l
是轮胎的纵向速度(即：轮胎沿其自身行进方向上的速度)，r是轮胎半径，ω是角速度；
[0239]
所述滑移角为：
[0240]
其中，轮胎的侧向速度为：vc＝v
y cos δ-v
x sin δ，
ꢀꢀꢀ
(31)
[0241]
轮胎的纵向速度为：v
l
＝v
y sin δ-v
x cos δ，
ꢀꢀꢀ
(32)
[0242]
且v
x
、vy分别是vc和v
l
在车身坐标系xoy下沿x轴方向、y轴方向的合速度，δ是车轮偏角；
[0243]
(补充说明：公式(27)至公式(32)为广义公式，同时适用于车辆前轮与车辆后轮的轮胎分析。)
[0244]
在车身坐标系xoy下，车辆前、后轮在x轴方向、y轴方向的速度可通过如下式子进行转换：
[0245][0246][0247][0248][0249]
上述中，v
yf
是车辆前轮在车身坐标系xoy下沿y轴方向的速度，v
yr
是车辆后轮在车身坐标系xoy下沿y轴方向的速度，v
xf
是车辆前轮在车身坐标系xoy下沿x轴方向的速度，v
xr
是车辆后轮在车身坐标系xoy下沿x轴方向的速度，是车辆在车身坐标系xoy下沿x轴方向的速度，是车辆在车身坐标系xoy下沿y轴方向的速度，是车辆航向角对时间的一阶导数，b1是车辆质心到其前轴的距离，b2是车辆质心到其后轴的距离；
[0250]
假设车辆前、后轴的载荷转移忽略不计，则：
[0251]
车辆前轮所受到的垂向载荷为：
[0252]
车辆后轮所受到的垂向载荷为：
[0253]
上述中，b1是车辆质心到其前轴的距离，b2是车辆质心到其后轴的距离，m是整车质量，g是重力加速度(这些参数都可以根据车辆的状态信息进行计算得到；在实际控制过程中，假设滑移率和路面摩擦系数μ是已知的)；
[0254]
由此得到，非线性车辆动力学微分方程为：
[0255]
其中，ζ(t)是t时刻横向控制器的状态量，其中，ζ(t)是t时刻横向控制器的状态量，是t时刻的横向控制器的控制量，横向控制器的控制量，是车辆在车身坐标系xoy下沿x轴方向的速度，是车辆在车身坐标系xoy下沿y轴方向的速度；是车辆航向角，是车辆航向角对时间的一阶导数；x是车辆在惯性坐标系xoy中x轴方向的坐标，y是车辆在惯性坐标系xoy中y轴方向的坐标；δf是车辆的前轮偏角；
[0256]
sb-2、基于非线性车辆动力学微分方程和模型预测控制理论，建立横向控制器的状态空间方程，及其目标函数和约束条件：
[0257][0258][0259][0260]
上述中，公式(40)是在离散时间模型下的表达式；是t时刻横向控制器的控制量，量，是t-1时刻横向控制器的控制量；是横向控制器控制量的增量，ζ(t)是t时刻横向控制器的状态量；ζ(t+1)是t+1时刻横向控制器的状态量；δf是车辆的前轮偏角，δδf是车辆前轮偏角的增量；是t时刻横向控制器的输出，是与横向控制器状态量对应的输出矩阵；
[0261]
考虑车辆在跟踪过程中的准确性、稳定性及舒适性所得横向控制器的目标函数如下：
[0262][0263]
上式中，是在t时刻求得的横向控制器的最优控制量，是t时刻求出的不同横向控制器控制时域内的最优控制量的增量序列，下标代表的是不同时刻；h
p
是横向控制器预测时域；hc是横向控制器控制时域；ε是松弛因子；为t时刻预测的t+i时刻横向控制器的控制输出；是t时刻预测的t+i时刻横向控制器的状态量(状态量即为系统的输出量)参考值；是t时刻预测
的t+i时刻横向控制器控制量的增量；是t时刻预测的t+i时刻横向控制器的控制量；是权重系数；q是横向控制器状态量的权重矩阵；g是横向控制器控制量增量的权重矩阵；s是横向控制器控制量的权重矩阵；
[0264]
为了对横向控制器的整个控制过程进行优化，在每一时刻均对以下优化模型进行求解：(求解该优化模型实际就是求解每一时刻的横向控制器控制量的增量，即：在每一个时刻都需要求出横向控制器控制时域内的控制量的增量序列，从而求出横向控制器控制量，对系统进行控制。)
[0265][0266]
关于车辆动力学方面的约束条件：
[0267][0268][0269][0270]
δ
t，t
＝ζ(t)；
ꢀꢀꢀ
(48)
[0271][0272][0273]
关于车辆的前轮偏角的约束条件：
[0274][0275]
关于车辆的前轮偏角增量的约束条件：
[0276][0277]
上述中，ζ
k+1，t
是t时刻预测的k+1时刻横向控制器的状态量，是车辆动力学模型表达式，ζ
k，t
是t时刻预测的k时刻横向控制器的状态量，是t时刻预测的k时刻横向控制器的控制量，是t时刻预测的k-1时刻横向控制器的控制量，是t时刻得到的k时刻横向控制器控制量的增量，是t时刻预测的k时刻横向控制器的输出，h
2ω
(ζ
k，t
)是车辆动力学相关约束(在简化的车辆二轮模型下与车辆状态量相关的动力学约束)，ω是角速度，δ
t，t
是t时刻横向控制器的状态量，ζ(t)是t时刻横向控制器的状态量，是t时刻预测的t-1时刻横向控制器的控制量，是t-1时刻横向控制器的控制量，是t时刻横向控制器的控制量，是t时刻横向控制器的控制量，是横向控制器控制量的下限，是横向控制器控制量的上限，是横向控制器控制量增量的下限，是横向控制器控制量增量的上限。
[0278]
本例中，所述纵向控制器是基于模型预测控制理论设计的双层控制器，包括上层控制器和下层控制器；所述上层控制器根据期望速度及车辆状态信息计算出期望加速度，并将计算出的期望加速度传递给下层控制器；所述下层控制器将接收到的期望加速度同当前空气阻力和滚动阻力的大小与车辆质量的比值进行比较，然后根据切换逻辑判断车辆应
当进行加速操作还是制动操作，将节气门开度值/制动压力值传给车辆，车辆进行相应操作后再将控制结果反馈给上层控制器，形成闭环控制。
[0279]
另外，本例还给出了一种车辆的横纵向综合控制器，所述车辆的横纵向综合控制器是采用本例所述的车辆的横纵向综合控制方法进行的；
[0280]
所述车辆的横纵向综合控制器包括速度规划器、横向控制器和纵向控制器；
[0281]
所述速度规划器是基于模型预测控制理论及车辆运动学模型建立的，用于生成与期望路径相对应的关于车辆的期望速度曲线，得到并输出期望速度；
[0282]
所述横向控制器是基于模型预测控制理论及车辆动力学模型建立的；所述横向控制器接收所述速度规划器输出的期望速度，结合期望路径和车辆状态信息计算出车辆的前轮偏角的增量，并将所计算的车辆的前轮偏角的增量信号传递给车辆，即所述横向控制器的控制输出是车辆的前轮偏角；
[0283]
所述纵向控制器是基于模型预测控制理论设计的双层控制器，包括上层控制器和下层控制器；所述纵向控制器接收所述速度规划器输出的期望速度，并结合车辆状态信息将接收的信息转换为期望制动压力/期望节气门开度信号传递给车辆，即所述纵向控制器的控制输出是车辆的制动/油门；
[0284]
所述纵向控制器的控制过程具体包括：所述上层控制器根据期望速度及车辆状态信息计算出期望加速度，并将计算出的期望加速度传递给下层控制器；所述下层控制器将接收到的期望加速度同当前空气阻力和滚动阻力的大小与车辆质量的比值进行比较，然后根据切换逻辑判断车辆应当进行加速操作还是制动操作，将节气门开度值/制动压力值传给车辆，车辆进行相应操作后再将控制结果反馈给上层控制器，形成闭环控制；
[0285]
所述横向控制器和所述纵向控制器的控制输出将同时给到车辆，车辆依据接收到的控制信号做出相应操作，并且将车辆状态信息反馈给横向控制器和纵向控制器；
[0286]
所述横向控制器和所述纵向控制器是通过期望速度耦合起来的，由此综合控制车辆按照期望速度运行同时跟踪期望路径。
[0287]
图1给出了本例车辆运动学模型的示意图。在惯性坐标系xoy下，(xr，yr)和(xf，yf)分别为车辆后轴和前轴的轴心坐标，为车体的横摆角(车辆航向角)，δf为车辆的前轮偏角，vr为车辆后轴中心速度(在运动学模型中将车辆两个后轮看作一个整体)，vf为车辆行进方向的速度(在运动学模型中将车辆两个前轮看作一个整体)，l为轴距。在速度规划中，把车辆看作一个质点，此时速度的方向跟航向角是相同的。
[0288]
图2给出了本例参考路径的示意图(即已知的路径图)。从该图能看出已知路径的形状，但不能直接得到已知路径上每一点在惯性坐标系xoy中x轴、y轴方向的坐标信息，路径曲率信息，路径擦系数等路径信息。
[0289]
图3给出了本例规划出的期望路径和基于该路径生成的期望速度曲线图，其中，实线是基于图2中的参考路径规划得到的期望路径，虚线是基于规划出的期望路径生成的期望速度曲线。从图3中可以明显看出，在前方有大曲率路段时，速度会在弯道前逐渐减小，以较低的速度通过弯道后再加速。
[0290]
本例将规划出的期望路径(如图3中的实线所示)输入速度规划器，生成与期望路径相对应的关于车辆的期望速度曲线(如图3中的虚线所示)，得到并输出期望速度控制序列(如图4所示，图中简记为速度序列)；纵向控制器接收速度规划器输出的期望速度，并结
合车辆状态信息得到期望加速度控制序列(如图5所示，图中简记为加速度序列)，进而转换为期望制动压力/期望节气门开度信号传递给车辆。
[0291]
图6给出了本例采用的车辆动力学模型示意图。图中，xoy为惯性坐标系，xoy为车身坐标系，f
xf
是车辆前轮受到在车身坐标系xoy下沿x轴方向的力，f
xr
是车辆后轮受到在车身坐标系xoy下沿x轴方向的力，f
yf
是车辆前轮受到在车身坐标系xoy下沿y轴方向的力，f
yr
是车辆后轮受到在车身坐标系xoy下沿y轴方向的力，f
cf
是车辆前轮受到的侧向力(即：车辆前轮受到沿垂直于车辆前轮行进方向的力)，f
cr
是车辆后轮受到的侧向力(即：车辆后轮受到沿垂直于车辆后轮行进方向的力)，f
lf
是车辆前轮受到的纵向力(即：车辆前轮受到沿车辆前轮行进方向的力)，f
lr
是车辆后轮受到的纵向力(即：车辆后轮受到沿车辆后轮行进方向的力)，δf是车辆的前轮偏角(即：在车身坐标系xoy下，车辆前轮行进方向与x轴方向的夹角)，δr是车辆的后轮偏角(即：在车身坐标系xoy下，车辆后轮行进方向与x轴方向的夹角)；v
lf
是车辆前轮的纵向速度(即：车辆前轮沿车辆前轮行进方向的速度)；v
cf
是车辆前轮的侧向速度(即：车辆前轮沿垂直于车辆前轮行进方向的速度)；vf是车辆行进方向的速度；αf是车辆前轮的滑移角；b1是车辆质心到其前轴的距离；b2是车辆质心到其后轴的距离；是车辆的横向速度(即：车辆沿垂直于车身方向的速度)；是车辆的纵向速度(即：车辆沿车身方向的速度)；是车辆航向角对时间的一阶导数。
[0292]
本例采用的车辆轮胎公式是魔术轮胎公式，其输入、输出情况如图7所示。
[0293]
图8给出了本例横向控制器在单独控制时的控制示意图。
[0294]
图9给出了本例纵向控制器在单独控制时的控制示意图。
[0295]
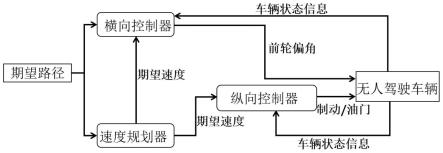
图10给出了本例车辆的横纵向综合控制器的控制示意图。
[0296]
补充说明：横向控制器、纵向控制器在解耦(图8、图9)与耦合(图10)情况下的控制区别：图8的横向控制器在单独跟踪控制时的路径是期望路径(如图3中的实线)，由于此时检测横向控制器的跟踪效果，所以一般会以匀速作为跟踪前提进行检测。图9的纵向控制器在单独跟踪控制的时候主要实现的是对期望速度的跟踪，此时的期望路径是一条直线，因为此时检测的是纵向控制器对期望速度的跟踪效果，不涉及到车辆的转向。由于横向控制器、纵向控制器二者在解耦情况下的跟踪效果并不理想，所以设计了本发明的横向控制器和纵向控制器耦合的综合控制器(即本发明的横纵向综合控制器，如图10所示)，横向控制器和纵向控制器的耦合是通过期望速度实现的，此时就要求车辆以期望速度跟踪期望路径，所以由速度规划器输出的期望速度分别传给横向控制器和纵向控制器，将二者耦合。
[0297]
上述结合附图对本发明进行了示例性描述，显然本发明的具体实现并不受本文所示的实施例限制。